En esta página encontrarás la explicación de qué son las rectas concurrentes, junto con ejemplos de rectas concurrentes.
Índice
¿Qué son las rectas concurrentes?
La definición matemática de las rectas concurrentes es la siguiente:
En geometría, las rectas concurrentes son dos o más rectas coplanarias que se cortan en un mismo punto (llamado punto de la concurrencia). Por lo tanto, un conjunto de rectas concurrentes solo tienen un punto en común.
Si estamos trabajando en el plano (en R2) dos rectas diferentes solo pueden ser coincidentes, paralelas o secantes. Entonces, todas las rectas secantes también son rectas concurrentes, ya que tienen un punto de intersección.
Si no te ha quedado claro el concepto anterior te recomiendo que le eches un vistazo a la definición de rectas secantes, donde encontrarás qué son este tipo de rectas y cómo saber si dos rectas son secantes o no.
En cambio, cuando operamos en el espacio (en R3) es más difícil hallar rectas concurrentes, porque es más complicado que 2, 3, 4,… rectas se corten en un mismo punto y que, además, estén contenidas en un mismo plano.
Por otro lado, el concepto de concurrencia no solo se aplica a las rectas: si dos o más objetos geométricos distintos comparten un punto significa que son concurrentes.
Ejemplo de rectas concurrentes
Una vez hemos visto el significado de las rectas concurrentes, veamos ahora un ejemplo de este tipo de rectas:
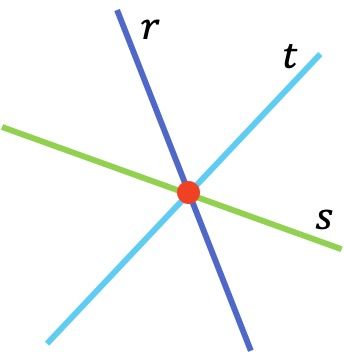
Como puedes ver en la representación gráfica de las rectas r, s y t, las tres líneas rectas son concurrentes porque se intersecan en un mismo punto (representado de color rojo).
Por otro lado, antes de acabar, si te ha gustado esta página puede que también estés interesado en las rectas en general. Pues un concepto muy importante sobre las rectas es calcular su ecuación, de hecho, en geometría analítica las ecuaciones de la recta se utilizan muy a menudo. Puedes ver cómo se halla dicha ecuación en la siguiente página: cómo calcular la ecuación de la recta que pasa por dos puntos.


Excelente la información
¡Gracias Miriam!
Excelente explicación 💯👌
¡Gracias Max! 😉
Muy buena explicación💯
¡Muchas gracias Emanuel! 😉
¿Me pueden demostrar la siguiente situación?
«Dos rectas concurrentes paralelas a un plano, determinan un plano que es paralelo al dado.»
Hola Jimena,
Para definir matemáticamente un plano se necesitan tres puntos diferentes del plano, una recta y un punto del plano, o dos rectas del plano. De modo que dos rectas concurrentes definen un plano completamente.
Además, el enunciado dice que estas dos rectas concurrentes son paralelos a un plano, por lo tanto, el plano que definen las dos rectas concurrentes también es paralelo a dicho plano.