En esta página se explica cómo se suman dos vectores en el plano, tanto gráficamente como numéricamente. Existen 3 maneras para sumarlos de manera gráfica: el método del paralelogramo, de la cabeza con cola y del polígono. Además, también encontrarás ejercicios resueltos de sumas de vectores y todas las propiedades de la suma vectorial.
Índice
¿Cómo sumar dos vectores gráficamente?
Básicamente, existen dos maneras de sumar vectores a partir de su representación gráfica. Con las dos formas se obtiene el mismo resultado, pero hay unos que prefieren sumarlos utilizando el método cabeza-cola y otros con el método del paralelogramo. Así que te explicaremos ambos métodos para que elijas el que prefieras. 😉
Por otra parte, estos dos métodos sirven para sumar dos vectores pero ¿qué pasa si queremos sumar más de dos vectores? Entonces tenemos que usar el método del polígono, que implica usar el método del paralelogramo de forma sucesiva. También encontrarás su explicación después de los métodos de la cabeza-cola y del paralelogramo.
Método o regla del paralelogramo
La regla del paralelogramo o método del paralelogramo (o incluso ley del paralelogramo) es un procedimiento gráfico que permite hallar la suma de dos vectores de manera muy simple. Los pasos que se deben seguir para aplicar este proceso son:
- En primer lugar, dibujamos los vectores y los posicionamos en el mismo punto de aplicación, es decir, situamos los orígenes de los dos vectores en el mismo punto.
- Después dibujamos en el extremo de un vector una recta paralela al otro vector. Y repetimos el paso con el otro vector. De manera que obtendremos el dibujo de un paralelogramo (de ahí viene el nombre de la regla).
- Finalmente, el resultado de la suma será el vector que va desde el origen común hasta el punto donde se cruzan las dos rectas paralelas.
Fíjate en el siguiente ejemplo genérico en el que se suman dos vectores con la regla del paralelogramo:
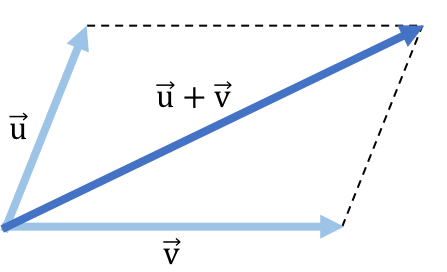
El resultado de la suma de los vectores es la diagonal del paralelogramo que forman junto con sus rectas paralelas.
Método de la cabeza y cola
El método de la cabeza y cola, o también conocido como método del triángulo, es otro procedimiento con el que se pueden sumar gráficamente dos vectores. En este caso, los pasos que se tienen que hacer son:
- Desplazar un vector de los que se suman y colocarlo de forma que su origen esté justo en el extremo del otro vector que se suma.
- El resultado de la suma vectorial es el segmento que va desde el inicio del primer vector sumado hasta el final del otro vector. Si te fijas, se completa un triángulo con los dos vectores sumados y el vector suma.
A continuación tienes un ejemplo de una suma de vectores con el método de la cabeza con cola:
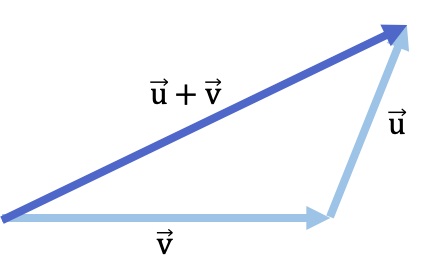
Método del polígono
Una vez hemos visto cómo resolver la suma de dos vectores gráficamente, vamos a ver cómo se hace cuando tenemos más de dos vectores.
Cuando queremos sumar tres o más vectores, existe una técnica para ir más rápido en el cálculo de la operación. Esta técnica se llama método del polígono y consiste en aplicar el método de la cabeza-cola sucesivamente:
- Primero tenemos que colocar cada vector a continuación de otro, de manera que el origen de un vector coincida con el extremo de otro vector. El orden en el que los colocamos es indiferente.
- Y el resultado de la suma es el vector que se obtiene al unir el inicio del primer vector con el extremo del último vector.
Fíjate en el siguiente ejemplo donde se suman 4 vectores:
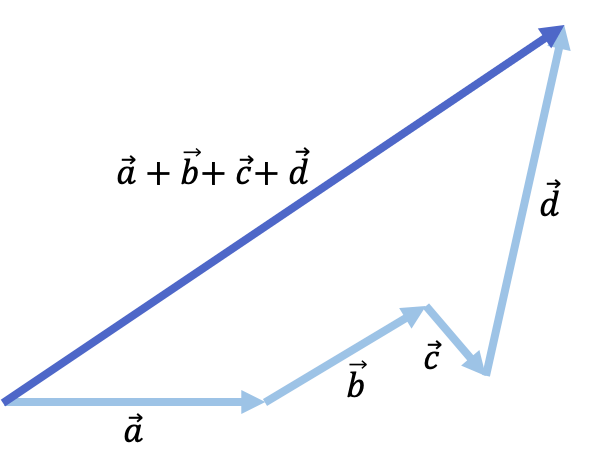
Calcular la suma de dos vectores numéricamente
Una vez ya sabemos sumar vectores geométricamente, vamos a ver cómo calcular una suma vectorial numéricamente o algebraicamente.
Para sumar dos vectores numéricamente se deben sumar sus respectivas componentes. O dicho con otras palabras, se suman las coordenadas X de los dos vectores entre sí y lo mismo con las coordenadas Y.
Por ejemplo, la suma entre los vectores y
es:
Por otro lado, hay que tener presente que sumar dos vectores vectorialmente no es lo mismo que sumar los módulos de los vectores, de hecho, los resultados son totalmente distintos. Puedes ver las diferencias entre las dos operaciones en las propiedades de la magnitud de un vector (también conocido como módulo de un vector).
Propiedades de la suma de vectores
La adición vectorial posee las siguientes características:
- Propiedad asociativa: poner paréntesis entre la suma de varios vectores no altera el resultado de la operación.
- Propiedad conmutativa: a diferencia de la resta de vectores, el resultado de la suma entre dos vectores es independiente del orden en el que se sumen.
- Propiedad del elemento opuesto: la suma de un vector más su opuesto, es decir su negado, es igual a 0.
- Propiedad del elemento neutro: evidentemente, cualquier vector más el vector nulo o cero es equivalente al propio vector:
Ejercicios resueltos de suma de vectores
Ejercicio 1
Calcula gráficamente la suma de los vectores y
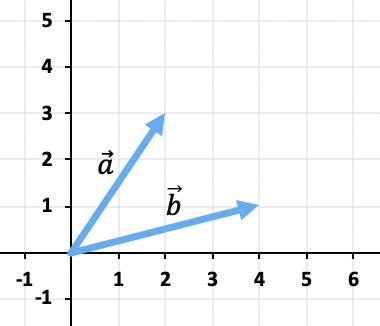
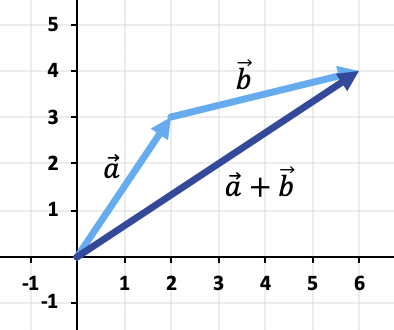
Para sumar los dos vectores utilizaremos la regla de la cabeza y cola. De manera que colocaremos el origen del vector en el extremo del vector
, y la suma será el vector que va desde el origen de coordenadas hasta el extremo de
Por lo tanto, el resultado de la suma vectorial es:
Ejercicio 2
Resuelve gráficamente la suma de los vectores y
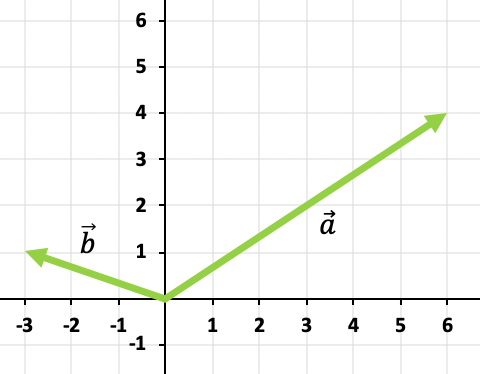
Para sumar los dos vectores utilizaremos la regla de la cabeza-cola. De modo que situaremos el origen del vector en el extremo del vector
, y el vector suma será el que va desde el origen de los ejes hasta el extremo de
Por lo tanto, el resultado de la suma vectorial es:
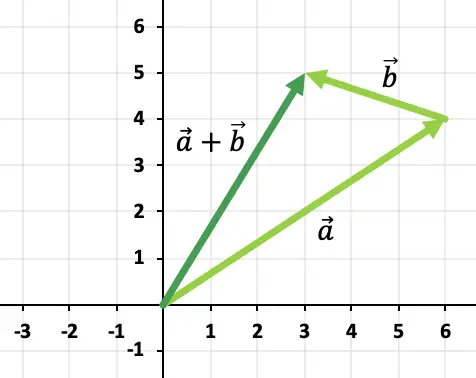
Ejercicio 3
Determina gráficamente el vector resultante de sumar todos los vectores representados en el gráfico:
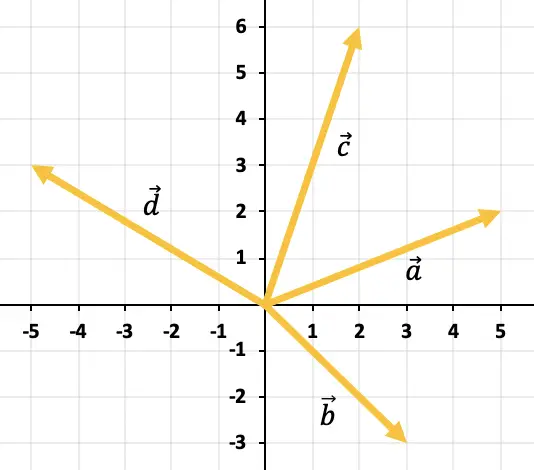
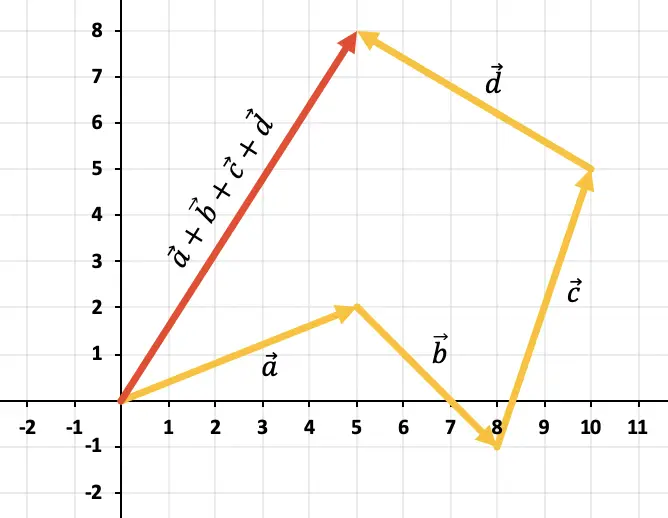
Para sumar más de 2 vectores a partir del gráfico hay que utilizar la regla del polígono. Por tanto, tenemos que desplazar los vectores y que queden de forma continuada, es decir, uno detrás del otro (el orden es indiferente). Entonces, la suma de todos los vectores será el vector que va desde el origen del primer vector hasta el extremo del último vector.
Así que el resultado de la suma de los 4 vectores es el vector representado de color rojo:
Ejercicio 4
Halla la suma de los siguientes vectores numéricamente:
Para sumar dos vectores numéricamente debemos sumar sus respectivas coordenadas:
Ejercicio 5
Calcula la suma de los siguientes vectores analíticamente:
Para sumar vectores numéricamente debemos sumar sus respectivas coordenadas:
