▷ Hallar la distancia entre dos rectas en el espacio ✅ (ejemplos)

En esta página encontrarás cómo se calcula la distancia entre dos rectas en el espacio (en R3), sean del tipo que sean (rectas paralelas, que se cruzan, coincidentes, secantes, perpendiculares, etc.). Además, podrás ver ejemplos y ejercicios resueltos paso a paso.

Índice

Cómo calcular la distancia entre dos rectas

La distancia entre dos rectas es la mínima distancia que hay entre cualquier punto de una recta con cualquier punto de la otra recta. Esta distancia corresponde a la longitud del segmento que va desde una recta hasta la otra recta y que, a la vez, es perpendicular a ambas rectas.

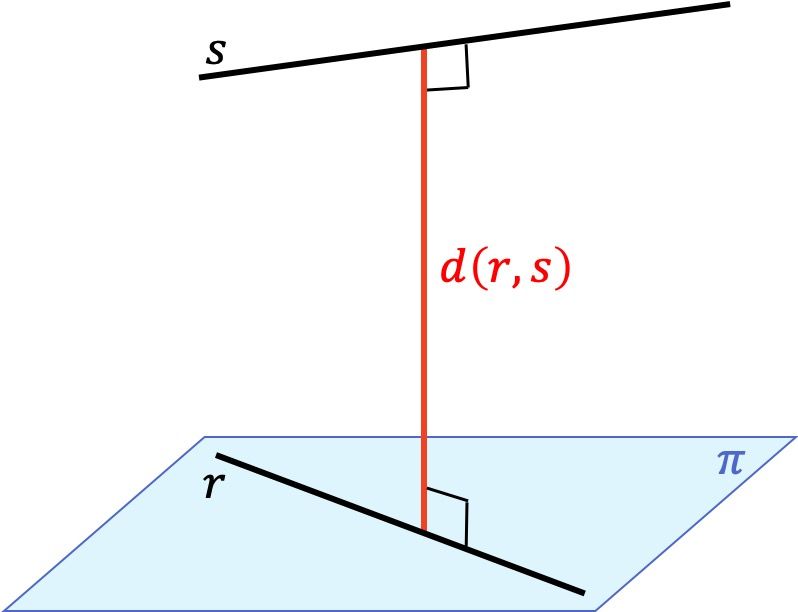
distancia entre dos rectas en el espacio (en R3)

Así pues, encontrar la distancia entre dos rectas distintas en un espacio tridimensional (3D) depende de la posición relativa entre ellas:

Si las dos rectas son coincidentes o secantes la distancia entre las dos rectas es igual a cero, ya que se cortan (como mínimo) en un punto.
Cuando las dos rectas son paralelas tenemos que coger cualquier punto de una de las rectas y calcular la distancia desde ese punto hasta la otra recta (más abajo dispones de un ejemplo de cómo se hace).
Si las dos rectas se cruzan en el espacio, debemos aplicar la fórmula de la distancia entre dos rectas que se cruzan (más abajo tienes la explicación detallada).

Entonces, para poder calcular la distancia entre dos rectas primero debemos saber qué tipo de rectas se trata y luego, según el caso, utilizar una fórmula u otra. Por lo tanto, es importante que ya domines cómo hallar la posición relativa de dos rectas en el espacio antes de seguir, pero si no recuerdas cómo se hacía en el enlace podrás ver una explicación muy completa junto con ejemplos y ejercicios resueltos paso a paso.

Cómo hallar la distancia entre dos rectas paralelas en el espacio

Calcular la distancia entre dos rectas paralelas en el espacio (en R3) se hace de la misma manera que en el plano (en R2): tenemos que coger un punto de cualquiera de las dos rectas y hallar la distancia que hay desde ese punto hasta la otra recta.

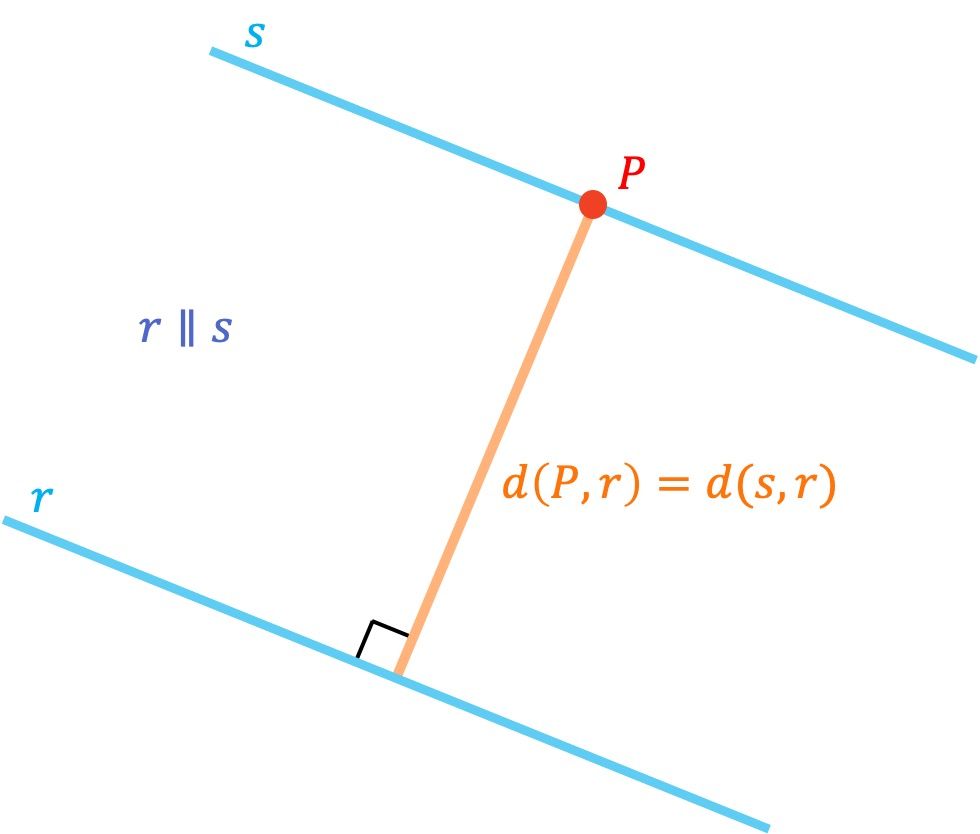
Entonces, la fórmula para calcular la distancia de un punto a una recta en 3 dimensiones (y que sirve para determinar la distancia entre dos rectas paralelas) es:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Donde:

$\lvert \vv{\text{v}}_r \rvert$ es módulo del vector director de la recta $r.$
$Q$ es un punto de la recta $r,$ $P$ un punto de la recta $s$ y $\vv{QP}$ el vector definido por ambos puntos
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$ es el módulo del producto vectorial entre los vectores $\vv{QP}$ y $\vv{\text{v}}_r$

A modo de ejemplo, vamos a resolver un problema de distancia entre 2 rectas paralelas en el espacio:

¿Cuál es la distancia entre las siguientes dos rectas paralelas?

$r: \ (x,y,z) = (2,1,1) + t(-1,3,2)$

$s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)$

Ambas rectas están expresadas en forma de ecuación vectorial, por lo tanto, podemos saber fácilmente el vector director y un punto de cada una de ellas:

$\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}$

Si tienes alguna duda de cómo se determina el vector director y un punto de una recta, te recomendamos que eches un vistazo a la explicación de la ecuación de la recta. Allí lo hemos explicado para todas las ecuaciones de la recta, ya que hallar el vector director y un punto que pertenezca a una recta depende del tipo de ecuación en que esté expresada la recta.

Ahora, para averiguar la distancia entre las dos rectas paralelas, debemos aplicar la fórmula de la distancia de un punto a una recta:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Así que por un lado calculamos el módulo del vector resultante del producto vectorial. Si tienes dudas de cómo se calcula, puedes consultar la fórmula del producto vectorial, donde, además, podrás ver ejemplos y ejercicios resueltos de esta operación entre vectores.

$\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)$

$\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}$

$\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}$

Y, por otra parte, hallamos el módulo del vector de la recta $r:$

$\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}$

Finalmente, sustituimos el valor de cada término en la fórmula y calculamos la distancia entre las rectas:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}$

Por lo tanto, la distancia entre las dos rectas es de 3,60 unidades.

Cómo determinar la distancia entre dos rectas que se cruzan en el espacio

Como hemos visto al principio, el método para determinar la distancia entre dos rectas que se cruzan es diferente al procedimiento para distancias entre rectas paralelas.

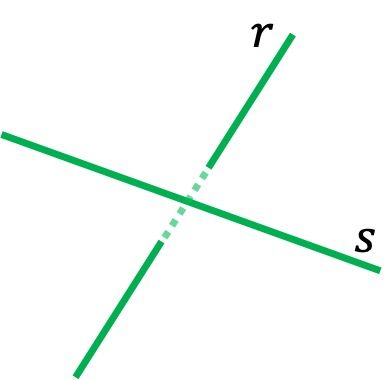
distancia entre rectas cruzadas en el espacio

Así pues, existen varios métodos para determinar la distancia que hay entre dos rectas que se cruzan en el espacio. En esta página solo te explicaremos un procedimiento, el más fácil, porque los otros dos métodos son más largos y complicados, de hecho, prácticamente ni se utilizan.

Sea el vector director y un punto cualquiera de dos rectas que se cruzan:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

La fórmula de la distancia entre dos rectas que se cruzan es:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Donde $\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$ es el valor absoluto del producto mixto de los vectores $\vv{\text{u}}, \vv{\text{v}}$ y el vector definido por los puntos $A$ y $B$ . Y, por otra parte, $\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$ es el módulo del producto vectorial entre los vectores directores de las dos rectas cruzadas.

Para que puedas ver cómo determinar la distancia entre dos rectas cruzadas, vamos a resolver un problema a modo de ejemplo:

¿Cuál es la distancia entre las siguientes dos rectas que se cruzan?

$r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}$

$s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}$

En primer lugar, tenemos que identificar el vector director y un punto de cada recta. Ambas rectas están expresadas en forma de ecuación continua, por tanto:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}$

Y ahora aplicamos la fórmula de la distancia entre dos rectas que se cruzan:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Por un lado resolvemos el producto mixto (o triple producto escalar):

$\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)$

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13$

Y, por otra parte, hallamos el módulo del producto vectorial (o producto cruz):

$\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}$

$\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}$

Por último, sustituimos el valor de cada término en la fórmula de la distancia entre dos rectas cruzadas:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}$

6 comentarios en “Distancia entre dos rectas en el espacio (en R3)”

Juan Fernando
06/04/2021 a las 12:58

Así de clarito, las matemáticas se saborean mejor que en el IES, pues en este van a matacaballo. Al no haber fijado bien los contenidos de la primera evaluación, he recurrido a vosotros.
Añado, además, lo que en otra ocasión leí a un joven afirmar que en estas webs le dísteis la confianza en aprobar, al contrario que en la enseñanza recibida en su IES. JuanF.

Responder
1. Geometría Analítica
  09/04/2021 a las 23:01
  
  ¡Muchas gracias por tu comentario Juan!
  
  Siempre intentamos explicar el temario lo mejor posible, para que sea fácil de entender. ¡Cualquier duda, aquí nos tienes!
Jorge
13/04/2021 a las 18:12

Este Curso me ha enseñado cosas que el colegio poco me ha enseñado y gracias a esto tengo mas idea de lo que en un Futuro Examen , puedo hacer , gracias a esto mis conocimeintos son mayores y podre aprobar todos los semestres

Responder
1. Geometría Analítica
  17/04/2021 a las 17:39
  
  ¡Nos alegramos de que te sea útil la página Jorge! ¡Siempre intentamos explicar cada tema lo mejor que podemos!
  ¡Seguro que apruebas e, incluso, sacarás muy buena nota! 💪💪💪
micaela
09/06/2022 a las 18:34

excelente información.

Responder
1. Geometría Analítica
  13/06/2022 a las 10:16
  
  ¡Gracias Micaela!

Cómo calcular la distancia entre dos rectas

Cómo hallar la distancia entre dos rectas paralelas en el espacio

Cómo determinar la distancia entre dos rectas que se cruzan en el espacio

6 comentarios en “Distancia entre dos rectas en el espacio (en R3)”

Deja un comentario Cancelar respuesta