▷ Hallar la ecuación de una circunferencia (fórmula y ejemplos)

En esta página encontrarás todo sobre la ecuación de la circunferencia: ecuación ordinaria, ecuación general, otros tipos de ecuaciones de la circunferencia, cuándo es correcta la ecuación de una circunferencia,… Además, verás ejemplos de cómo hallar la ecuación de una circunferencia y podrás practicar con ejercicios resueltos.

Índice

Ecuación ordinaria de la circunferencia

Antes de ver cuál es la ecuación de la circunferencia, vamos a recordar el concepto de circunferencia:

La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.

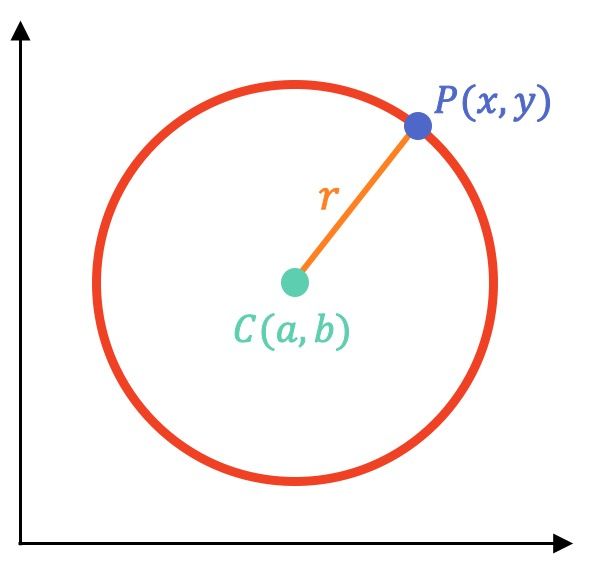
cual es la ecuacion de la circunferencia

Por tanto, todos los puntos de una circunferencia están a una misma distancia de su centro.

Además, la circunferencia es una de las cuatro secciones cónicas junto con la elipse, la parábola y la hipérbola. Es decir, se puede obtener una circunferencia cortando un cono con un plano paralelo a su base.

La manera más fácil de describir una circunferencia en el plano cartesiano es a partir de su ecuación ordinaria. Así pues, la fórmula de la ecuación ordinaria de la circunferencia es la siguiente:

La ecuación ordinaria de la circunferencia es:

$(x-a)^2+(y-b)^2=r^2$

Donde:

$r$ es el radio de la circunferencia.
$a$ y $b$ son las coordenadas del centro de la circunferencia: $C(a,b)$

Aunque no haremos la demostración porque es un poco tediosa, esta ecuación se puede obtener a partir del teorema de Pitágoras.

Veamos cómo se calcula la ecuación ordinaria de una circunferencia con un ejemplo:

Determina la ecuación ordinaria de la circunferencia de radio 5 cuyo centro es el punto $C(3,-1).$

La fórmula de la ecuación ordinaria de una circunferencia es:

$(x-a)^2+(y-b)^2=r^2$

Por tanto, solamente tenemos que sustituir la incógnita $r$ por el valor del radio, y las incógnitas $a$ y $b$ por las coordenadas X e Y respectivamente del centro de la circunferencia:

$(x-3)^2+(y-(-1))^2=5^2$

Así que la ecuación ordinaria de la circunferencia es:

$\bm{(x-3)^2+(y+1)^2=25}$

Ecuación general de la circunferencia

Otro tipo de ecuación de la circunferencia es la ecuación general, de hecho, es la que más se usa. A continuación vamos a ver cómo obtener la ecuación general de cualquier circunferencia a partir de su ecuación ordinaria.

Dada la ecuación ordinaria de una circunferencia:

$(x-a)^2+(y-b)^2=r^2$

Si desarrollamos las igualdades notables (o productos notables):

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

Ahora realizamos 3 cambios de variables:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

Y finalmente conseguimos la ecuación general de la circunferencia:

$x^2+y^2+Ax+By+C=0$

Por lo tanto, la fórmula de la ecuación general de la circunferencia es:

$x^2+y^2+Ax+By+C=0$

Donde el centro de la circunferencia es:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

Y el radio de la circunferencia es:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

De modo que esta ecuación de la circunferencia siempre se obtiene a través de la ecuación ordinaria. A continuación tienes un ejemplo para ver cómo se hace:

Determina la ecuación general de la circunferencia de radio 6 cuyo centro es el punto $C(2,4).$

Primero de todo, debemos hallar la ecuación ordinaria de la circunferencia. Para ello, utilizamos su fórmula:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

Y ahora operamos hasta encontrar la ecuación general de la circunferencia, es decir, hasta que no podamos simplificar más:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

De manera que la ecuación general de la circunferencia es:

$\bm{x^2+y^2-4x-8y-16=0}$

Aunque no lo pedía el problema, ahora podemos calcular el centro y el radio de la ecuación hallada para comprobar que está bien.

Para determinar el centro de la circunferencia utilizamos su fórmula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

Efectivamente, el centro de la circunferencia coincide con el del encunciado.

Verificamos también el radio de la circunferencia con su fórmula:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

Y el radio también es igual al del enunciado. Por tanto, la ecuación de la circunferencia calculada es la correcta.

Existencia de una circunferencia

No todas las ecuaciones en forma de $x^2+y^2+Ax+By+C=0$ corresponden a una circunferencia. Entonces, para que este tipo de expresión sea verdaderamente la ecuación de una circunferencia se deben de cumplir las siguientes 3 condiciones:

Los coeficientes de $x^2$ y de $y^2$ deben ser iguales a 1. Ten en cuenta que si las dos variables tuviesen delante un número diferente de uno pero ambas con el mismo número, se podría dividir toda la ecuación por ese número para que sus coeficientes fuesen 1.
La ecuación no puede tener término $xy.$
La siguiente expresión debe ser positiva:
$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0$

Otros tipos de ecuaciones de la circunferencia

Las dos ecuaciones de la circunferencia que hemos visto, la ecuación ordinaria y la ecuación general, son las que más se utilizan para expresar una circunferencia matemáticamente en el plano (en R2). Sin embargo, existen más tipos de ecuaciones para describir este objeto geométrico, a continuación tienes la explicación de cada una de ellas.

Ecuación canónica de la circunferencia

La ecuación canónica, o ecuación reducida, de una circunferencia sirve para describir cualquier circunferencia que tiene su centro en el origen de coordenadas, es decir, en el punto (0,0). Dicha ecuación es de la siguiente manera:

$x^2+y^2=r^2$

Si, además, el radio fuese equivalente a la unidad (1), la ecuación de la circunferencia sería:

$x^2+y^2=1$

Esta última ecuación corresponde a la circunferencia goniométrica, también llamada circunferencia unidad o circunferencia unitaria. Se trata de la circunferencia de radio 1 centrada en el origen de coordenadas.

Ecuaciones de dos circunferencias concéntricas

Dos ecuaciones concéntricas son aquellas que tienen el centro en el mismo punto. Y lo único diferente que tienen dos circunferencias concéntricas es el radio.

Por lo tanto, para que esta condición se cumpla, las ecuaciones de dos circunferencias concéntricas son exactamente iguales excepto sus términos independientes, que deben ser distintos.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

Por ejemplo, las siguientes dos circunferencias son concéntricas, ya que todos sus coeficientes son idénticos menos los términos independientes:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

Ecuación paramétrica de la circunferencia

Al igual que la recta, la ecuación de una circunferencia también se puede parametrizar con las funciones trigonométricas del seno y del coseno. Así pues, las ecuaciones paramétricas de la circunferencia son:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

Donde el punto $(a,b)$ es el centro de la circunferencia y $r$ es su radio.

Ejercicios resueltos de la ecuación de una circunferencia

Ejercicio 1

Calcula la ecuación general de la circunferencia de radio 5 cuyo centro está en el punto $C(-1,2).$

Ver solución

Para averiguar la ecuación general de la circunferencia, primero debemos hallar su ecuación ordinaria. Para ello, utilizamos la fórmula de la ecuación ordinaria de una circunferencia:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

Una vez conocemos la ecuación ordinaria, operamos hasta encontrar la ecuación general de la circunferencia:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

De modo que la ecuación general de la circunferencia es:

$\bm{x^2+y^2+2x-4y-20=0}$

Ejercicio 2

Para cada una de las siguientes circunferencias, halla las coordenadas de su centro y la longitud de su radio.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

Ver solución

Circunferencia A)

$(x-2)^2+(y+5)^2=36$

La circunferencia está expresada en forma de ecuación ordinaria, cuya fórmula es:

$(x-a)^2+(y-b)^2=r^2$

Por tanto, la coordenadas del centro de la circunferencia son:

$C(a,b)$

$\bm{C(2,-5)}$

Y su radio es:

$r^2=36$

$\bm{r=6}$

Circunferencia B)

$x^2+y^2+8x-10y+1 = 0$

Está circunferencia está expresada en forma de ecuación general, por lo tanto para calcular las coordenadas de su centro debemos utilizar la siguiente fórmula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

Por otro lado, la fórmula para hallar el radio de la circunferencia es:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

Circunferencia C)

$x^2+y^2=4$

La circunferencia está expresada en forma de ecuación ordinaria, cuya fórmula es:

$(x-a)^2+(y-b)^2=r^2$

Por tanto, la coordenadas del centro de la circunferencia son:

$C(a,b)$

En este caso no la ecuación no tiene término $a$ ni $b,$ por tanto está centrada en el origen de coordenadas:

$\bm{C(0,0)}$

Y su radio es:

$r^2=4$

$\bm{r=2}$

Ejercicio 3

¿Cuáles de las siguientes ecuaciones son la ecuación de una circunferencia?

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

Ver solución

Para que una expresión sea la ecuación de un circunferencia se debe cumplir lo siguiente:

1. Los coeficientes de $x^2$ y de $y^2$ deben ser iguales a 1.
2. La ecuación no puede tener término $xy.$
3. $\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0$

Así que debemos comprobar que se cumplen las tres condiciones para cada ecuación.

Ecuación A)

$x^2+y^2+4x-6y-1=0$

Los coeficientes de $x^2$ e $y^2$ son 1 y la ecuación no tiene término $xy.$ Por lo que solo nos queda verificar la tercera condición:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0$

$\displaystyle \left(\frac{4}{2}\right)^2+\left(\frac{-6}{2}\right)^2-(-1)>0$

$\displaystyle 2^2+\left(-3\right)^2+1>0$

$\displaystyle 4+9+1>0$

$\displaystyle 14>0$

La ecuación verifica las 3 condiciones, por tanto, es la ecuación de una circunferencia.

Ecuación B)

$x^2+y^2+5x+5y+2xy-4 = 0$

La ecuación tiene término con $xy,$ con lo que la ecuación no corresponde a una circunferencia.

Ecuación C)

$2x^2+2y^2-8x+4y+2=0$

Los coeficientes de $x^2$ e $y^2$ no son 1, pero podemos transformar la ecuación dividiendo todos los términos:

$x^2+y^2-4x+2y+1=0$

De esta forma ahora los coeficientes de $x^2$ e $y^2$ sí son 1 y, además, la ecuación no tiene término $xy.$ Por lo que solo nos queda corroborar la tercera condición:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0$

$\displaystyle \left(\frac{-4}{2}\right)^2+\left(\frac{2}{2}\right)^2+1>0$

$\displaystyle (-2)^2+\left(1\right)^2+1>0$

$\displaystyle 4+1+1>0$

$\displaystyle 6>0$

La ecuación verifica las 3 condiciones, por lo tanto, es la ecuación de una circunferencia.

Ecuación D)

$x^2+y^2+x+2y+6=0$

Los coeficientes de $x^2$ e $y^2$ son 1 y la ecuación no tiene término $xy.$ Con lo que solo nos queda verificar la tercera condición:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0$

$\displaystyle \left(\frac{1}{2}\right)^2+\left(\frac{2}{2}\right)^2-6>0$

$\displaystyle 0,25+1-6>0$

$\displaystyle -4,75 \ \cancel{>} \ 0$

La ecuación no cumple con la última condición, de modo que no es la ecuación de una circunferencia.

Ejercicio 4

Determina la ecuación de la circunferencia que pasa por los siguientes tres puntos:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

Ver solución

La ecuación general de cualquier circunferencia es:

$x^2+y^2+Ax+By+C=0$

Por tanto, tenemos que sustituir las coordenadas de los puntos en la ecuación de la circunferencia para encontrar los parámetros $A,$ $B$ y $C.$

Con el primer punto de encontramos el coeficiente $C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

Con el segundo punto hallamos el coeficiente $A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

Y a partir del tercer punto encontramos el coeficiente $B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

En conclusión, la ecuación general de la circunferencia es:

$\bm{x^2+y^2-3x+y=0}$

Ejercicio 5

Si los extremos opuestos de una circunferencia son los siguientes dos puntos:

$A(2,3) \qquad B(6,-1)$

¿Cuál es la ecuación ordinaria de la circunferencia?

Ver solución

Si los dos puntos son extremos de la circunferencia, su centro será el punto medio entre esos dos puntos:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

Por otra parte, el diámetro de la circunferencia será la distancia entre los dos puntos, que se puede calcular mediante el módulo del vector que forman los dos puntos:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

Y el radio de la circunferencia es la mitad del diámetro:

$r = \cfrac{\sqrt{32}}{2}$

Por lo tanto, la ecuación ordinaria de la circunferencia es:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

Para terminar, si te ha sido útil este artículo seguramente también te interesen nuestras páginas de la hipérbola (matemáticas) y la parábola (matemáticas). En ellas encontrarás una explicación detallada de qué es la hipérbola y la parábola, sus ecuaciones, sus características, ejemplos, ejercicios resueltos…

6 comentarios en “Ecuación de la circunferencia”

Luis j mora g
18/08/2022 a las 15:02
Excelente documento
Responder
1. Geometría Analítica
  19/08/2022 a las 12:21
  ¡Gracias Luis!
2. Juan Carlos AIRA
  29/08/2023 a las 12:53
  Coincido con Luis.
  Fue muy ùtil
Isabel
19/08/2022 a las 13:19
Me encanto la explicación lo entendí muy bien pero me gustaría que añadieran cómo graficarla así estaría más completa, pero lo demás estuvo excelente gracias
Responder
1. Geometría Analítica
  22/08/2022 a las 12:42
  Gracias por tu comentario Isabel, me alegra de que te gustara. ¡Apuntamos tu sugerencia para mejorar el post!
Gael
07/01/2024 a las 10:35
Waos, es una excelente página, llevo un rato estudiando desde esta página y realmente se explican muy detalladamente los procedimientos y el por que de las cosas
Responder

Ecuación ordinaria de la circunferencia

Ecuación general de la circunferencia

Existencia de una circunferencia

Otros tipos de ecuaciones de la circunferencia

Ecuación canónica de la circunferencia

Ecuaciones de dos circunferencias concéntricas

Ecuación paramétrica de la circunferencia

Ejercicios resueltos de la ecuación de una circunferencia

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

6 comentarios en “Ecuación de la circunferencia”

Deja un comentario Cancelar respuesta