▷ Cómo calcular el producto mixto de 3 vectores (ejemplos)

En esta página explicamos qué es el producto mixto de tres vectores (o triple producto escalar) y cómo se calcula. También verás ejemplos, ejercicios y problemas resueltos sobre este tipo de operación entre vectores. Y, además, encontrarás las propiedades y las aplicaciones del producto mixto.

Índice

¿Qué es el producto mixto de tres vectores?

El producto mixto de tres vectores, también conocido como triple producto escalar, es una multiplicación sucesiva entre tres vectores en la que intervienen dos tipos de operaciones diferentes: el producto escalar y el producto vectorial. De forma que la combinación de ambas operaciones vectoriales da como resultado un escalar (un número real).

Concretamente, el producto mixto consiste en calcular el producto vectorial de dos vectores y, posteriormente, en multiplicar vectorialmente el resultado obtenido por un tercer vector. Así escrito puede parecer muy complicado, pero en realidad no lo es tanto, fíjate en la fórmula del triple producto escalar:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

Como puedes ver en su fórmula, el producto mixto de tres vectores se denota con dos corchetes.

¿Cómo calcular el producto mixto de tres vectores?

La fórmula del triple producto escalar es la que acabamos de ver en el apartado anterior, sin embargo, no se suele utilizar para determinar el producto mixto de tres vectores ya que existe otra manera más fácil y rápida:

Sean 3 vectores cualesquiera:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

Para calcular el producto mixto entre tres vectores simplemente se tiene que resolver el determinante 3×3 formado por las componentes de los vectores:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

Para que veas un ejemplo de cómo se calcula, vamos a hallar el producto mixto de los siguientes tres vectores:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

Para determinar el producto mixto, construimos un determinante de orden 3 colocando los vectores como filas de la matriz:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

Y ahora tan solo debemos resolver el determinante de la matriz, para ello puedes usar cualquier método. Nosotros en este caso aplicaremos la regla de Sarrus (pero también se puede hacer por adjuntos o cofactores):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

Para demostrar que los dos procedimientos son equivalentes, vamos a calcular el producto mixto de los mismos vectores mediante su definición:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

Nosotros te recomendamos que calcules el producto mixto a través del determinante de los vectores, porque es más rápido y hay menos posibilidades de equivocarse. Pero, como puedes ver, el resultado es igual independientemente del método que uses, así que utiliza el que prefieras. 👍

Interpretación geométrica del producto mixto

Una vez ya sabes cómo hallar el producto mixto de tres vectores puede que te estés preguntando… ¿y para qué sirve el producto mixto? Pues en matemáticas tiene dos usos principalmente: calcular el volumen de un paralelepípedo y el volumen de un tetraedro.

El volumen de un paralelepípedo es igual al valor absoluto del producto mixto de los vectores que marcan las 3 dimensiones del cuerpo geométrico.

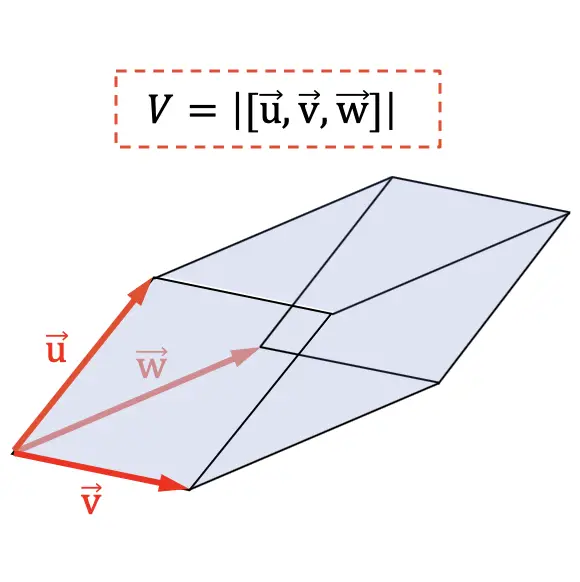
ejemplo de producto mixto de tres vectores o triple producto escalar

Otra aplicación del producto mixto es determinar el volumen de un tetraedro. Ya que geométricamente la sexta parte del valor absoluto del producto mixto representa el volumen de un tetraedro:

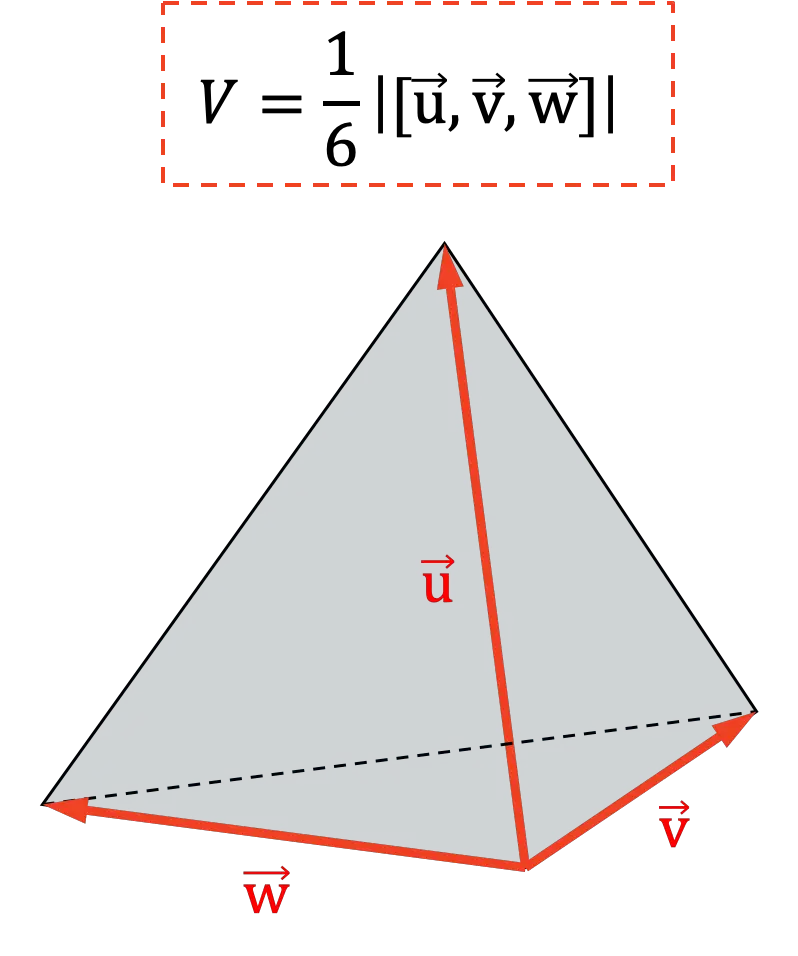
Propiedades del producto mixto o triple producto escalar

El producto mixto, o triple producto escalar, tiene las siguientes características:

En general, un cambio en el orden de los vectores del producto mixto implica también un cambio de signo. Por lo tanto, el orden de los vectores del producto mixto es importante.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

Sin embargo, si alteramos el orden de manera cíclica el signo no varia:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

En un espacio tridimensional (en R3), el producto mixto de tres vectores linealmente dependientes o coplanarios (que pertenecen al mismo plano) es igual a 0.

Ejercicios resueltos de productos mixtos

Ejercicio 1

Dados 3 vectores:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

Calcula el producto mixto de los tres vectores:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

Ver solución

Para hallar su producto mixto, debemos resolver el determinante compuesto por las coordenadas de los vectores:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

Ejercicio 2

Dados 3 vectores:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

Determina el producto mixto entre los tres vectores:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

Ver solución

Para encontrar su producto mixto, debemos resolver el determinante que tiene por filas las coordenadas cartesianas de los vectores:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

Ejercicio 3

Calcula el volumen del paralelepípedo cuyos 3 de sus lados son los siguientes vectores:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

Ver solución

El volumen de un paralelepípedo es igual al valor absoluto del producto mixto de 3 de los vectores que tiene por aristas. Por tanto, primero calculamos el producto vectorial triple de los vectores:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

De modo que el volumen del paralelepípedo es el valor absoluto del resultado del producto mixto:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

Ejercicio 4

Calcula el volumen del tetraedro que tiene como vértices los siguientes puntos:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

Ver solución

En primer lugar, calculamos los vectores que representan las aristas del tetraedro:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

El volumen de un tetraedro es equivalente a un sexto del valor absoluto del producto mixto de 3 de los vectores que tiene por aristas. Por lo tanto, primero calculamos el producto mixto de los vectores hallados:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

De modo que el volumen del tetraedro será una sexta parte del valor absoluto del producto mixto:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

Producto mixto de tres vectores (o triple producto escalar)

¿Qué es el producto mixto de tres vectores?

¿Cómo calcular el producto mixto de tres vectores?

Interpretación geométrica del producto mixto

Propiedades del producto mixto o triple producto escalar

Ejercicios resueltos de productos mixtos

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Deja un comentario Cancelar respuesta