Producto vectorial de dos vectores (o producto cruz)

En esta página se explica qué es el producto vectorial de dos vectores y cómo se calcula. También verás cómo saber la dirección y el sentido del producto vectorial mediante la regla de la mano derecha (o del sacacorchos). Y, además, encontrarás las utilidades que tiene este tipo de operación, así como ejemplos, ejercicios y problemas resueltos paso a paso.

¿Qué es el producto vectorial de dos vectores?

En matemáticas, el producto vectorial es una operación entre dos vectores en un espacio tridimensional (en R3). El resultado de esta operación vectorial es un vector de dirección perpendicular a los dos vectores que se multiplican, y de módulo igual al producto de los módulos de los vectores multiplicadores por el seno del ángulo que forman. Es decir, su fórmula es:

\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)

Como ves en la fórmula anterior, el producto vectorial se denota con una \bm{\times}, es por eso que también se llama producto cruz. A veces también se dice producto vectorial de Gibbs, ya que fue quien lo inventó.

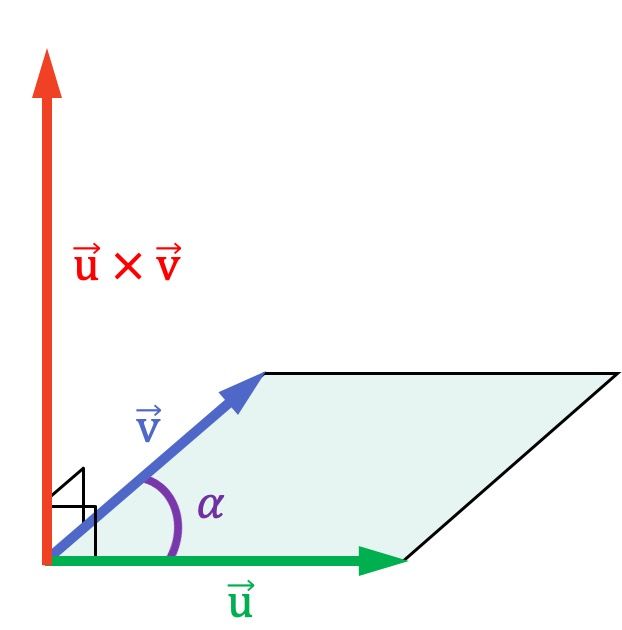
Como puedes apreciar en la representación gráfica anterior, el producto vectorial es perpendicular a los dos vectores que están multiplicando y, en consecuencia, es normal al plano que los contiene.

Fórmula para calcular el producto vectorial de dos vectores

Si conocemos las coordenadas cartesianas de los vectores, la manera más fácil de calcular su producto vectorial es resolviendo un determinante 3×3. Fíjate cómo se hace:

Sean dos vectores cualesquiera:

\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)

Su producto vectorial es:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}

Donde los vectores \vv{i}, \vv{j},\vv{k} son los vectores unitarios en los sentidos de los ejes X, Y, Z respectivamente.

Veamos un ejemplo de cómo calcular el producto vectorial entre dos vectores:

\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)

Para determinar el producto vectorial entre los vectores, debemos hacer el siguiente determinante de orden 3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}

En este caso, resolveremos el determinante por adjuntos o cofactores (también se podría utilizar la regla de Sarrus):

\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}

Por lo tanto, el resultado del producto vectorial de los dos vectores es:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}

Determinar la dirección y el sentido del producto vectorial

A veces no necesitamos saber las componentes del vector resultante del producto vectorial, sino que solo hallando su módulo, su sentido y su dirección es suficiente. Esto suele suceder en física, sobre todo en el cálculo de fuerzas.

Así pues, existen varias reglas para hallar la dirección y el sentido del producto vectorial, las más conocidas son la regla de la mano derecha, ya sea con tres dedos o con toda la mano, y la regla del sacacorchos (o tornillo). Puedes usar cualquiera de ellas así que no hace falta que te las sepas todas, aún así te explicaremos las tres reglas para que tú te quedes con la que prefieras. 😉

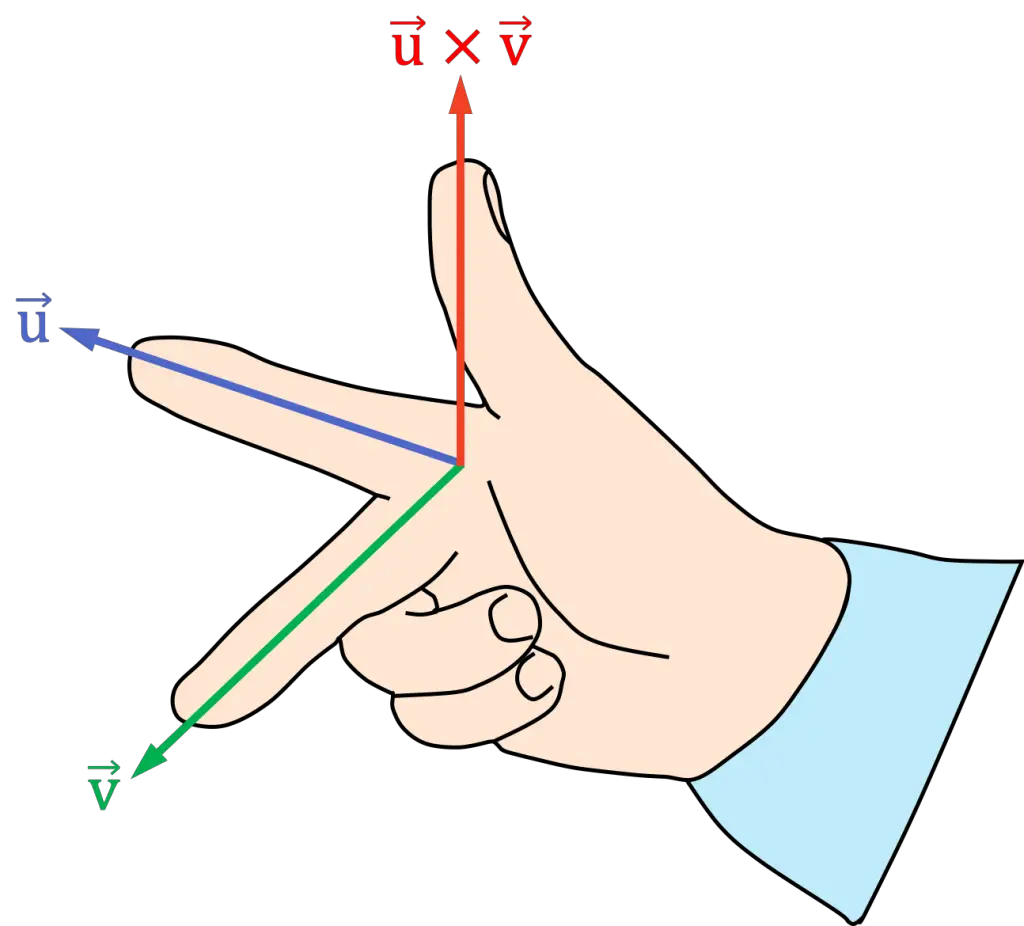
Regla de la mano derecha (3 dedos)

La versión de la regla o ley de la mano derecha con 3 dedos consiste en hacer los siguientes pasos:

  1. Coloca el dedo índice de la mano derecha en la dirección del primer vector del producto vectorial (\vv{\text{u}}).
  2. Coloca el dedo medio (o corazón) de la mano derecha en la dirección del segundo vector del producto vectorial (\vv{\text{v}}).
  3. La posición resultante del dedo pulgar señala la dirección y el sentido del producto vectorial (\vv{\text{u}}\times\vv{\text{v}}).

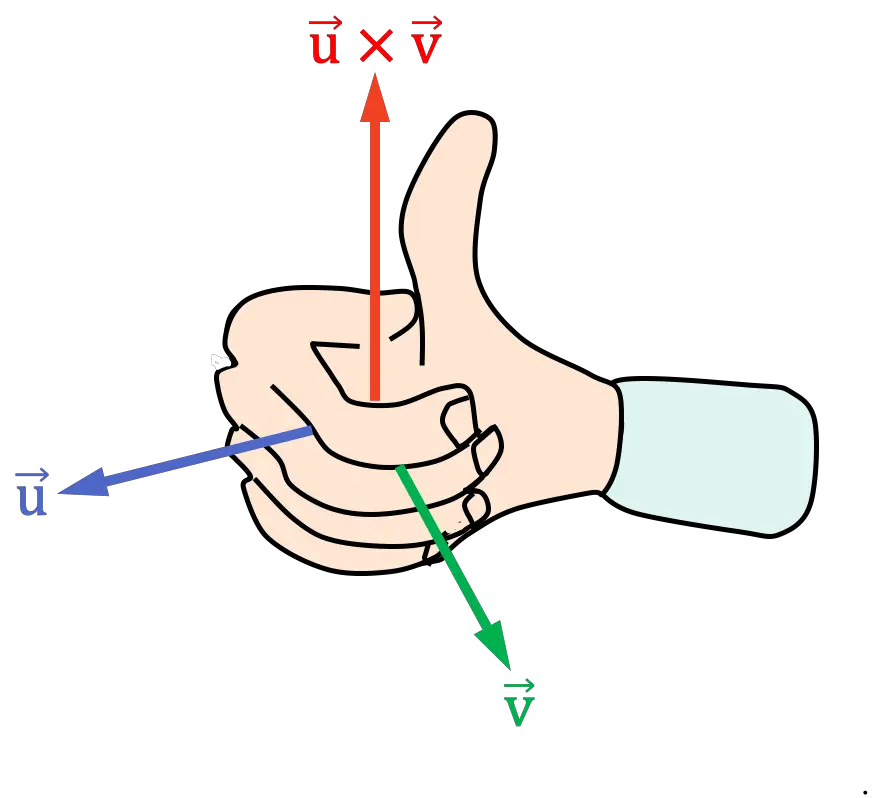
Regla de la mano derecha (palma de la mano)

La versión de la regla o ley de la mano derecha con la palma de la mano es muy similar a la regla anterior. Para aplicarla se deben seguir los siguientes pasos:

  1. Pon tu mano derecha apuntando con los dedos en la misma dirección que el primer vector del producto vectorial (\vv{\text{u}}).
  2. Cierra tu mano derecha moviendo tus dedos hacia el segundo vector del producto vectorial (\vv{\text{v}}). Se debe cerrar la mano por el lado en el que el ángulo (o distancia) entre los vectores es menor.
  3. La posición resultante del dedo pulgar determina el sentido y la dirección del producto vectorial (\vv{\text{u}}\times\vv{\text{v}}).

regla de la mano derecha producto vectorial

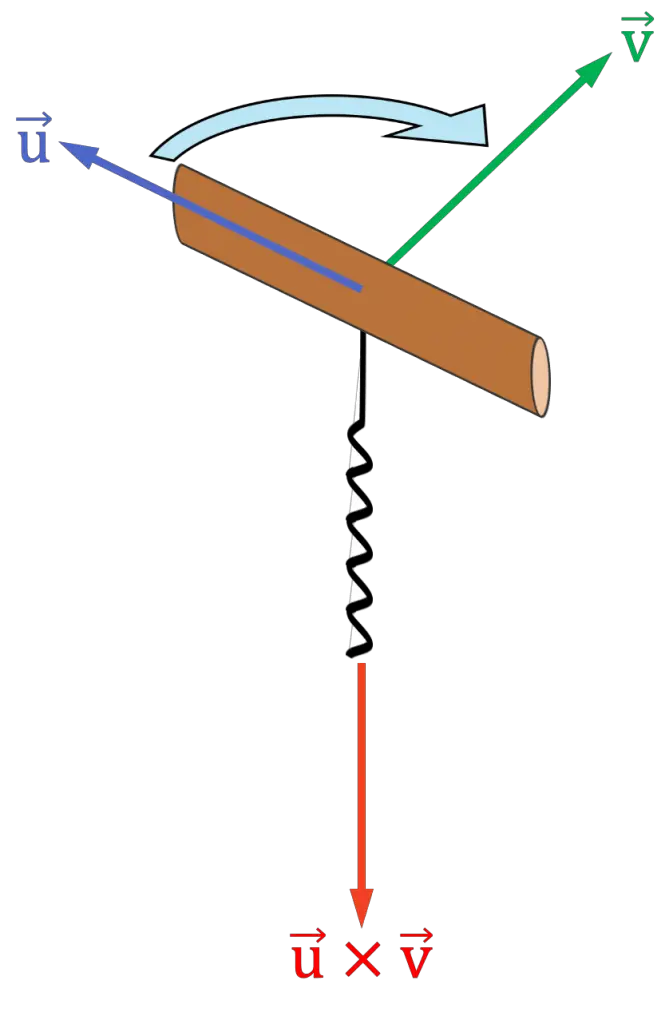
Regla del sacacorchos

La regla del sacacorchos o del tornillo es parecida a la regla de la mano derecha usando toda la palma de la mano. El procedimiento es el siguiente:

  1. Usando tu imaginación, sitúa un sacacorchos (o un tornillo) con el mango apuntando en la misma dirección que el primer vector del producto vectorial (\vv{\text{u}}).
  2. Luego gira el sacacorchos hacia el segundo vector del producto vectorial (\vv{\text{v}}) como si fueras a meterlo dentro de un corcho. Debes girar el sacacorchos por el lado en el que el recorrido entre los vectores es menor.
  3. La dirección en la que apunte el espiral del sacacorchos será la dirección y el sentido del producto vectorial (\vv{\text{u}}\times\vv{\text{v}}).

regla del sacacorchos o tornillo

Propiedades del producto vectorial de dos vectores

El producto vectorial de dos vectores tiene las siguientes características:

  • Propiedad anticonmutativa: el orden de los vectores que intervienen en el producto vectorial no es indiferente, porque el signo varia en función de ello.

\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}

  • Propiedad distributiva respecto a la suma y a la resta de vectores:

\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}

\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}

  • Propiedad homogénea: multiplicar un vector del producto vectorial por un escalar (un número real) es equivalente a multiplicar el resultado del producto vectorial por dicho escalar.

k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})

  • El vector resultante del producto vectorial es perpendicular a los dos vectores que habían intervenido en la operación.

\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}

  • Además, si los dos vectores son ortogonales se cumplen las siguientes ecuaciones:

\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}

  • El producto vectorial de dos vectores paralelos es igual al vector nulo (o cero).

\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0

  • Si no conocemos el ángulo que forman dos vectores, el módulo de su producto vectorial también se puede calcular mediante la siguiente expresión:

\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}

Calcular el área de un paralelogramo o un triángulo mediante el producto vectorial

Geométricamente, el módulo del producto vectorial de dos vectores coincide con el área del paralelogramo que tiene como lados esos dos vectores. Por lo tanto, se puede usar el producto vectorial para calcular el área de un paralelogramo.

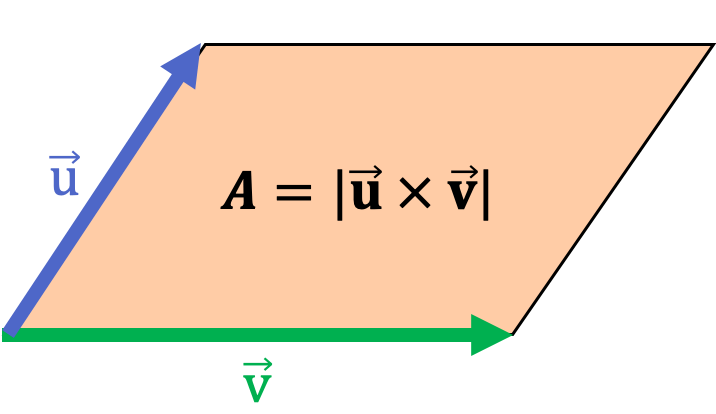
producto vectorial de dos vectores en el espacio

Además, la diagonal de un paralelogramo lo divide en dos triángulos, o dicho de otra forma, un triángulo es la mitad de un paralelogramo. De modo que el área de un triángulo es la mitad del módulo del producto vectorial cogiendo como vectores dos de sus lados.

producto vectorial de dos vectores en r2

Recordemos que el módulo de un vector en un espacio de 3 dimensiones es la raíz de la suma de los cuadrados de sus coordenadas:

\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}

Estas son dos de las aplicaciones del producto vectorial de dos vectores en el campo de las matemáticas. Sin embargo, aún tiene más utilidades, por ejemplo en física se usa para calcular el campo magnético.

Ejercicios resueltos de productos vectoriales de vectores

Ejercicio 1

Calcula el producto vectorial entre los siguientes dos vectores:

\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)

Para determinar el producto vectorial entre los vectores, debemos resolver el siguiente determinante de dimensión 3×3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}

En este caso, resolveremos el determinante por adjuntos o cofactores (pero también se podría utilizar la regla de Sarrus):

\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}

De manera que el resultado del producto vectorial de los dos vectores es:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}

 

Ejercicio 2

Halla el producto vectorial entre los siguientes dos vectores:

\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)

Para encontrar el producto vectorial entre los dos vectores, debemos resolver el siguiente determinante 3×3:

\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}

En este caso, resolveremos el determinante por adjuntos o cofactores (aunque se podría usar la regla de Sarrus indistintamente):

\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}

De manera que el resultado del producto vectorial entre los dos vectores es:

\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}

 

Ejercicio 3

Conociendo los módulos de dos vectores y el ángulo que forman:

|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º

Determina el módulo del producto vectorial de los dos vectores.

Podemos calcular fácilmente el módulo del producto vectorial entre los dos vectores aplicando la fórmula:

\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}

 

Ejercicio 4

A partir de los siguientes vectores contenidos en el plano de la pantalla:

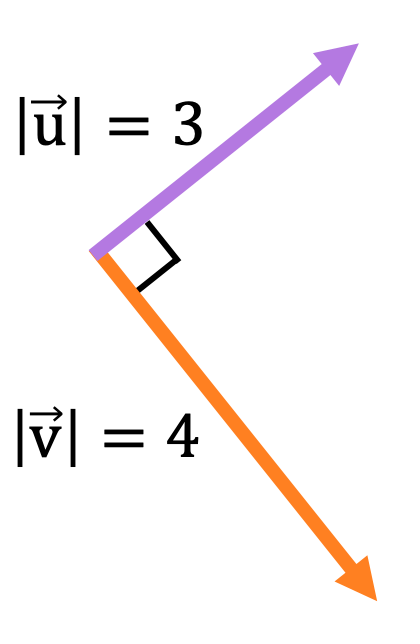
producto vectorial de dos vectores online

Calcula el módulo, la dirección y el sentido del vector resultante de la siguiente operación vectorial:

\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert

Los dos vectores son perpendiculares, por lo que el módulo del producto vectorial será:

\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}

Por otro lado, el vector resultante del producto vectorial es perpendicular a los dos vectores que participan en la operación, por lo tanto, su dirección será perpendicular a la pantalla.

Y, por último, utilizando la regla de la mano derecha (o del sacacorchos) se puede deducir que el sentido del vector resultante será hacia dentro de la pantalla.

 

Ejercicio 5

Calcula el área del paralelogramo que tiene como dos de sus lados a los siguientes vectores:

\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)

El área de un paralelogramo coincide con el módulo del producto vectorial de los vectores que lo forman. Así que calculamos el producto vectorial de los vectores:

\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}

Y luego su módulo:

A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}

 

Ejercicio 6

Encuentra el área del triángulo cuyos vértices son los siguientes puntos:

A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)

Primero de todo, debemos calcular los vectores que forman los lados del triángulo:

\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)

\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)

El área de un triángulo es la mitad del módulo del producto vectorial de los vectores que lo forman. Así que calculamos el producto vectorial de los vectores:

\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}

Después su módulo:

\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19

Y, finalmente, el área del triángulo será la mitad del módulo:

A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}

 

7 comentarios en “Producto vectorial de dos vectores (o producto cruz)”

  1. RODOLFO GODOSY ROSAS

    me gusta lo sencillo , basico y porque rescata un sentido rapido e intuitivo, suficiente para ir adelante en la ciencia y en cualquier carrera de ingenieria.

    Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio