Calcular el producto escalar de dos vectores

En esta página verás qué es y cómo calcular el producto escalar de dos vectores. También encontrarás cómo se encuentra el ángulo que forman dos vectores mediante el producto escalar y, además, todas las propiedades del producto escalar. Finalmente, podrás practicar con ejemplos y ejercicios resueltos paso a paso.

Cómo calcular el producto escalar entre dos vectores

En matemáticas, el producto escalar es una operación vectorial que multiplica dos vectores y los transforma en un un número real. Así pues, existen dos formas de calcular el producto escalar de dos vectores:

Si sabemos las coordenadas de dos vectores, se puede calcular su producto escalar multiplicando las componentes X y las componentes Y entre ellas y luego sumando los resultados. Es decir, si tenemos dos vectores:

\vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)

El producto escalar entre ellos es:

\displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y

Por ejemplo, el producto escalar entre los dos siguientes vectores es:

\vv{\text{u}} = (1,2) \qquad \vv{\text{v}} = (-1,3)

\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(1,2)\cdot (-1,3) \\[1.5ex]&=1\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -1+6 \\[1.5ex] & =\bm{5} \end{aligned}

Esta es una manera de hallar el producto escalar entre dos vectores. Sin embargo, también existe otro método:

En cambio, si conocemos el módulo y el ángulo entre dos vectores, se puede determinar el producto escalar entre los dos vectores calculando el producto de sus módulos por el coseno del ángulo que forman:

\displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(\alpha )

Donde \lvert \vv{\text{u}} \rvert y \lvert \vv{\text{v}} \rvert son los módulos de los vectores \vv{\text{u}} y \vv{\text{v}} respectivamente y \alpha el ángulo que forman.

Recordamos que el módulo de un vector es la raíz de los cuadrados de sus componentes:

\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}

A modo de ejemplo, vamos a resolver el producto escalar de dos vectores cuyos módulos y ángulo entre ellos son:

\displaystyle \lvert \vv{\text{u}} \rvert =3 \qquad \lvert \vv{\text{v}} \rvert = 4 \qquad \alpha=60º

\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}} & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(\alpha ) \\[1.5ex] &= 3 \cdot 4 \cdot \cos(60º)\\[1.5ex] & = 3 \cdot 4 \cdot 0,5 \\[1.5ex] &= \bm{6} \end{aligned}

Por otro lado, el producto escalar también se conoce como producto interno, producto interior o producto punto.

Nota: no hay que confundir el producto escalar con el producto vectorial porque, aunque tienen nombres similares, son conceptos totalmente diferentes.

Encontrar el ángulo entre dos vectores utilizando el producto escalar

Una vez hemos visto la definición del producto escalar, puede que te estés preguntando ¿y para qué sirve la multiplicación de dos vectores? Pues una de las aplicaciones del producto escalar es calcular el ángulo que forman dos vectores.

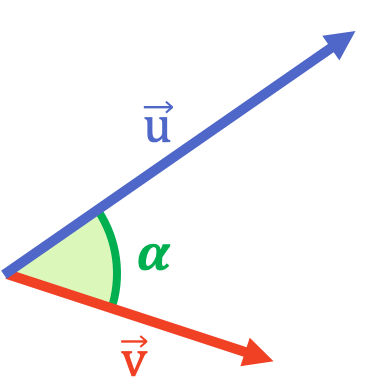
angulo entre dos vectores a partir del producto escalar

Al despejar el coseno de la fórmula del producto escalar obtenemos:

\definecolor{taronjaquadreejemplo}{HTML}{FF9800}\newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}\end{empheq}

Vamos a ver cómo se hace mediante un ejemplo:

  • Encuentra el ángulo que hay entre los siguientes dos vectores:

\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,5)

Primero tenemos que hallar el módulo de ambos vectores:

\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ 4^2+2^2}= \sqrt{20}

\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ (-1)^2+5^2}= \sqrt{26}

Ahora usamos la fórmula para calcular el coseno del ángulo que hay entre los dos vectores:

\displaystyle \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}=\cfrac{ 4\cdot (-1) + 2\cdot 5}{\sqrt{20}\cdot \sqrt{26}} = \cfrac{6}{\sqrt{520}} = 0,26

Finalmente, hallamos el ángulo correspondiente haciendo la inversa del coseno mediante la calculadora:

\displaystyle \cos^{-1}(0,26) = \bm{74,93º}

Por lo tanto, los vectores forman un ángulo de 74,93º.

Propiedades del producto escalar de dos vectores

El producto escalar tiene las siguientes características:

  • Propiedad conmutativa: el orden en el que se multiplican los vectores es indiferente.

\displaystyle \vv{\text{u}} \cdot \vv{\text{v}} =\vv{\text{v}} \cdot \vv{\text{u}}

  • Propiedad distributiva: el producto escalar es distributivo respecto a la suma y la resta de vectores:

\displaystyle \vv{\text{u}}( \vv{\text{v}}+ \vv{\text{w}} )=\vv{\text{u}} \cdot \vv{\text{v}}+ \vv{\text{u}} \cdot \vv{\text{w}}

\displaystyle \vv{\text{u}}( \vv{\text{v}}- \vv{\text{w}} )=\vv{\text{u}} \cdot \vv{\text{v}}- \vv{\text{u}} \cdot \vv{\text{w}}

  • Propiedad asociativa: podemos multiplicar el producto escalar por una constante antes o después de realizar la operación, ya que los resultados son equivalentes:

\displaystyle k\cdot (\vv{\text{u}} \cdot \vv{\text{v}}) = (k\cdot\vv{\text{u}}) \cdot \vv{\text{v}} =\vv{\text{u}} \cdot (k\cdot\vv{\text{v}})

  • Si dos vectores son ortogonales (o perpendiculares) entonces su producto escalar es nulo. Esta propiedad se puede demostrar fácilmente porque dos vectores perpendiculares forman un ángulo de 90º, y el coseno de 90º es igual a 0:

\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}} & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(90º ) \\[1.5ex] &=\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot 0 \\[1.5ex] &= 0 \end{aligned}

  • Por contra, si dos vectores son paralelos entonces su producto escalar da lo mismo que el producto de sus módulos. Esta propiedad también se puede comprobar de manera fácil ya que dos vectores con la misma dirección forman un ángulo de 0º, cuyo coseno es igual a 1:

\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}} & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(0º) \\[1.5ex] &=\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot 1 \\[1.5ex] &= \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \end{aligned}

  • Por último, el producto escalar de un vector por sí mismo es equivalente a su módulo elevado al cuadrado:

\displaystyle\vv{\text{u}} \cdot \vv{\text{u}} & = \lvert \vv{\text{u}} \rvert ^2

Ejercicios resueltos de productos escalares entre dos vectores

Ejercicio 1

Calcula el producto escalar en el plano de los siguientes dos vectores:

\vv{\text{u}} = (4,-3) \qquad \vv{\text{v}} = (5,2)

Para calcular el producto escalar de dos vectores debemos multiplicar sus coordenadas X y sus coordenadas Y entre sí y después sumar los resultados:

\displaystyle \begin{aligned}\vv{\text{u}} \cdot \vv{\text{v}} & = (4,-3)\cdot (5,2) \\[1.5ex] & = 4\cdot 5 + (-3) \cdot 2 \\[1.5ex] & = 20-6\\[1.5ex] & =\bm{14} \end{aligned}

 

Ejercicio 2

Determina el producto escalar de dos vectores cuyos módulos y ángulo que forman son:

\displaystyle \lvert \vv{\text{u}} \rvert =6 \qquad \lvert \vv{\text{v}} \rvert = 3 \qquad \alpha=45º

Como sabemos sus módulos y su ángulo entre ellos, podemos aplicar directamente la fórmula del producto escalar:

\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}} & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(\alpha ) \\[1.5ex] &= 6 \cdot 3 \cdot \cos(45º)\\[1.5ex] & = 6 \cdot 3 \cdot 0,71 \\[1.5ex] &= \bm{12,73} \end{aligned}

 

Ejercicio 3

¿Cuál es el ángulo entre los siguientes dos vectores?

\displaystyle \vv{\text{u}}=(3,8) \qquad \vv{\text{v}} =(-4,1)

En primer lugar, tenemos que calcular el módulo de ambos vectores:

\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ 3^2+8^2}= \sqrt{73}

\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ (-4)^2+1^2}= \sqrt{17}

Utilizamos la fórmula para calcular el coseno del ángulo que forman los vectores:

\displaystyle \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}=\cfrac{ 3\cdot (-4) + 8\cdot 1}{\sqrt{73}\cdot \sqrt{17}} = \cfrac{-4}{\sqrt{1241}} = -0,11

Y, por último, hallamos el ángulo correspondiente haciendo la inversa del coseno con la calculadora:

\displaystyle \cos^{-1}(-0,11) = \bm{96,52º}

 

Ejercicio 4

Dados los siguientes dos vectores:

\displaystyle \vv{\text{u}}=(5,2) \qquad \vv{\text{v}} =(-1,6)

Calcula la siguiente operación:

4 \bigl(\vv{\text{u}} \cdot\vv{\text{v}}\bigr)

Primero tenemos que resolver el producto escalar de dentro del paréntesis y luego hacer la multiplicación por el escalar de afuera:

4 \bigl(\vv{\text{u}} \cdot\vv{\text{v}}\bigr)

4 \bigl((5,2) \cdot (-1,6) \bigr)

4 \bigl(5 \cdot (-1) + 2 \cdot 6 \bigr)

4 \bigl(-5 + 12 \bigr)

4 \cdot 7

\bm{28}

 

Ejercicio 5

Dados los siguientes tres vectores bidimensionales:

\displaystyle \vv{\text{u}}=(-2,6) \qquad \vv{\text{v}} =(4,-3)\qquad \vv{\text{w}} =(-1,2)

Calcula la siguiente operación:

\vv{\text{w}} \cdot \bigl( 5 \vv{\text{u}}- 2 \vv{\text{v}}\bigr)

Primero de todo multiplicamos los vectores por los escalares de dentro del paréntesis:

\vv{\text{w}} \cdot \bigl( 5 \vv{\text{u}}- 2 \vv{\text{v}}\bigr)

(-1,2) \cdot \bigl( 5 (-2,6)- 2(4,-3)\bigr)

(-1,2) \cdot \bigl( (-10,30)- (8,-6)\bigr)

Ahora hacemos la resta de vectores:

(-1,2) \cdot (-10 -8,30-(-6))

(-1,2) \cdot (-18,36)

Y, para acabar, resolvemos el producto escalar:

(-1)\cdot (-18) + 2 \cdot 36

18 + 72

\bm{90}

 

Ejercicio 6

Calcula el valor de k para que los siguientes vectores sean perpendiculares:

\displaystyle \vv{\text{u}}=(-2,-3) \qquad \vv{\text{v}} =(k,6)

Dos vectores que son perpendiculares forman un ángulo de 90º. De modo que el coseno del ángulo tiene que valer cero, ya que cos(90º)=0. Por tanto:

\displaystyle \cos(90º) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}

\displaystyle 0=\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}

El denominador de la fracción está dividiendo todo el lado derecho de la ecuación, así que podemos pasarlo multiplicando al otro lado:

\displaystyle 0 \cdot \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert =\vv{\text{u}} \cdot \vv{\text{v}}

\displaystyle 0 =\vv{\text{u}} \cdot \vv{\text{v}}

Ahora resolvemos el producto escalar:

\displaystyle 0 =(-2,-3) \cdot (k,6)

\displaystyle 0 =-2 \cdot k + (-3)\cdot 6

\displaystyle 0 =-2 k -18

Y, finalmente, despejamos la incógnita:

\displaystyle 2k =-18

\displaystyle k =\cfrac{-18}{2}

\displaystyle \bm{k =-9}

 

Ejercicio 7

Calcula los ángulos \alpha , \beta y \gamma que forman los lados del siguiente triángulo:

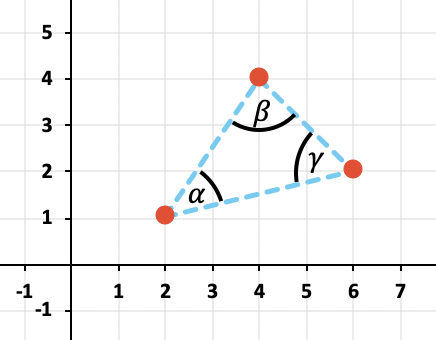
ejercicios y problemas resueltos paso a paso del producto escalar de dos vectores

Los vértices que componen el triángulo son los siguientes puntos:

A(2,1) \qquad B(4,4) \qquad C(6,2)

Para calcular los ángulos internos del triángulo, podemos calcular los vectores de cada uno de sus lados y luego hallar el ángulo que forman a través de la fórmula del producto escalar.

Por ejemplo, para encontrar el ángulo \alpha calculamos los vectores de sus lados:

\vv{AB} = B - A = (4,4)-(2,1)= (2,3)

\vv{AC} = C - A = (6,2)-(2,1)= (4,1)

Y hallamos el ángulo que forman los dos vectores mediante la fórmula del producto escalar:

\lvert \vv{AB} \rvert = \sqrt{2^2+3^2} = \sqrt{13}

\lvert \vv{AC} \rvert = \sqrt{4^2+1^2} = \sqrt{17}

\displaystyle \cos(\alpha) =\cfrac{\vv{AB} \cdot \vv{AC}}{\lvert \vv{AB} \rvert \cdot \lvert \vv{AC} \rvert}=\cfrac{ 2\cdot 4 + 3\cdot 1}{\sqrt{13}\cdot \sqrt{17}} = \cfrac{11}{\sqrt{221}} =0,74

\bm{\alpha = 42,27º}

Ahora repetimos el mismo procedimiento para determinar el ángulo \beta:

\vv{BC} = C - B = (6,2)-(4,4)= (2,-2)

\lvert \vv{BC} \rvert = \sqrt{2^2+(-2)^2} = \sqrt{8}

\displaystyle \cos(\beta) =\cfrac{\vv{AB} \cdot \vv{BC}}{\lvert \vv{AB} \rvert \cdot \lvert \vv{BC} \rvert}=\cfrac{ 2\cdot 2 + 3\cdot (-2)}{\sqrt{13}\cdot \sqrt{8}} = \cfrac{-2}{\sqrt{104}} =-0,20

\bm{\beta = 101,31º}

Finalmente, para encontrar el último ángulo podemos volver a hacer el mismo procedimiento. Sin embargo, todos los ángulos de un triángulo deben sumar 180º grados, por tanto:

\gamma = 180 -42,27-101,31 = \bm{36,42º}

 

4 comentarios en “Calcular el producto escalar de dos vectores”

  2. flor

    hola como estan.
    estaba haciendo los ejercicios y en el ejercicio 3: a ustedes les da un resultado el angulo de 96,52 grados….
    a mi me dio de resultado 96,31 grados.

    Responder
    1. Geometría Analítica

      Hola Flor,

      ¡Seguramente el ejercicio lo tengas bien resuelto! La diferencia en el resultado seguramente es debido a que has utilizado unos decimales diferentes, porque la diferencia es muy pequeña. Por eso lo más seguro es que hayas resuelto bien el problema.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio