¿Cuáles son todas las ecuaciones de la recta? (fórmulas y ejercicios)

Aquí encontrarás las fórmulas de todos los tipos de ecuaciones de la recta. También, podrás ver ejemplos de cómo se calculan y, además, practicar con ejercicios resueltos de las ecuaciones de la recta.

Índice

¿Cuáles son todas las ecuaciones de la recta?

Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Así pues, para expresar analíticamente cualquier recta en el plano (en R2) se utilizan las ecuaciones de la recta, y para hallarlas únicamente se necesita un punto que pertenezca a la recta y el vector director de dicha recta. Con tan solo estos dos elementos geométricos se pueden encontrar absolutamente todas las distintas ecuaciones de la recta, que son las siguientes:

Las ecuaciones de la recta son la ecuación vectorial, las ecuaciones paramétricas, la ecuación continua, la ecuación implícita (o general), la ecuación explícita, la ecuación punto-pendiente y la ecuación canónica (o segmentaria).

Todos los tipos de ecuaciones de la recta sirven para lo mismo: representar matemáticamente una recta. Pero cada ecuación de la recta tiene sus propiedades y, por lo tanto, dependiendo del problema es mejor usar una u otra.

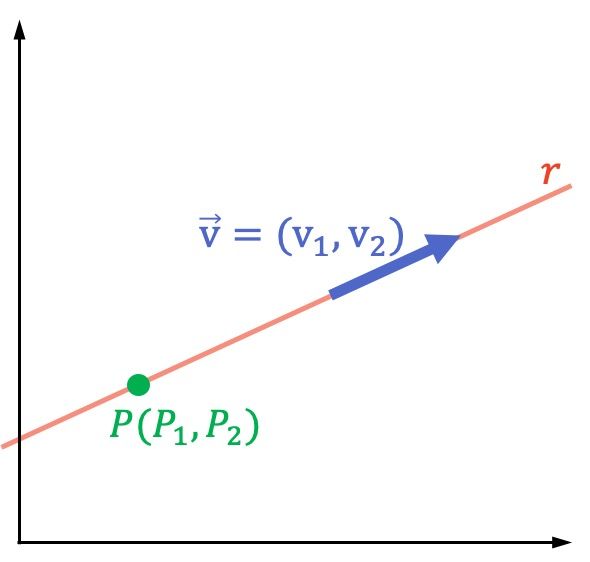
Una vez hemos visto el concepto de las ecuaciones de la recta, pasamos ahora a analizar las características de cada tipo de ecuación de la recta en concreto. A continuación tienes una explicación detallada de los diferentes tipos de ecuaciones de la recta, pero si quieres puedes ir directamente al final a la tabla resumen con las fórmulas de todas las ecuaciones de la recta.

Ecuación vectorial de la recta

Si $\vv{\text{v}}$ es el vector director de la recta y $P$ un punto que pertenece a la recta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La fórmula de la ecuación vectorial de la recta es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ es un escalar (un número real) cuyo valor depende de cada punto de la recta.

Esta es la ecuación vectorial de la recta en el plano, es decir, cuando trabajamos con puntos y vectores de 2 coordenadas (en R2). Sin embargo, si estuviésemos haciendo cálculos en el espacio (en R3) tendríamos que añadir una componente más a la ecuación de la recta:

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

Ecuaciones paramétricas de la recta

Las ecuaciones paramétricas de una recta se pueden obtener a partir de su ecuación vectorial:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Primero multiplicamos el parámetro $t$ por el vector director de la recta:

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

Luego sumamos las coordenadas X e Y:

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

Y, finalmente, despejando cada variable por separado conseguimos las ecuaciones paramétricas de la recta:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ es un escalar (un número real) cuyo valor depende de cada punto de la recta.

Al igual que antes, estas son las ecuaciones paramétricas de la recta en el plano (en R2), pero para hallar las ecuaciones parmétricas de la recta en el espacio (en R3) tendríamos que añadir una ecuación más para la tercera variable Z:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

Ecuación continua de la recta

La ecuación continua de cualquier recta se puede deducir a partir de sus ecuaciones paramétricas:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

Si despejamos el parámetro $t$ de cada ecuación paramétrica obtenemos las siguientes expresiones:

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E Igualando las dos ecuaciones resultantes obtenemos la ecuación continua de la recta:

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

En definitiva, la ecuación continua de la recta es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Esta fórmula es para la ecuación continua de la recta cuando trabajamos con 2 dimensiones (en 2D). Pero si estuviésemos realizando operaciones en 3 dimensiones (3D) tendríamos que añadir una componente más a la ecuación de la recta:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

Ecuación implícita o general de la recta

Si $\vv{\text{v}}$ es el vector director de la recta y $P$ un punto que pertenece a la recta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La fórmula de la ecuación implícita, general o cartesiana de la recta es:

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
El coeficiente $A$ es la segunda componente del vector director de la recta: $A=\text{v}_2}$
El coeficiente $B$ es la primera componente del vector director cambiada de signo: $B=-\text{v}_1}$
El coeficiente $C$ se calcula sustituyendo el punto conocido $P$ en la ecuación de la recta.

A parte de con la fórmula, también se puede obtener la ecuación implícita de una recta multiplicando en cruz las fracciones de la ecuación continua.

Ecuación explícita de la recta

La fórmula de la ecuación explícita de la recta es:

Donde:

$m$ es la pendiente de la recta.
$n$ su ordenada en el origen, es decir, la altura a la que corta el eje Y.

En el apartado de abajo verás cómo se determinan los parámetros $m$ y $n$ de la recta. Pero, en particular, otra forma de encontrar la ecuación explícita es a través de la ecuación implícita; para ello simplemente se debe despejar la incógnita $y$ de la ecuación implícita.

Significado de los parámetros m y n

Como hemos visto en la definición de la ecuación explícita de la recta, el parámetro $m$ es la pendiente de la recta y $n$ su ordenada en el origen. Pero… ¿qué significa esto? Veámoslo a partir de la representación gráfica de una recta:

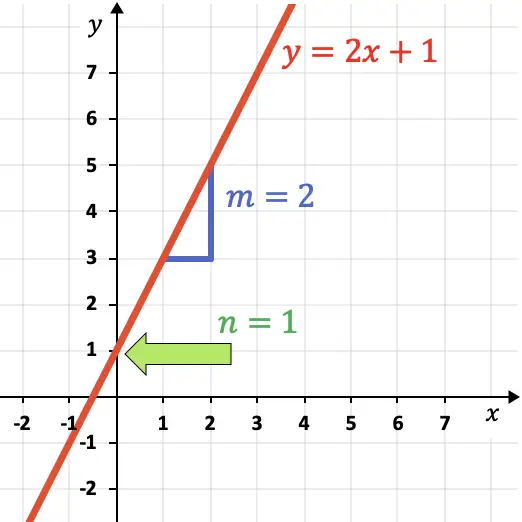
cual es la ecuacion explicita de la recta y=mx+b

El término independiente $\bm{n}$ es el punto de corte de la recta con el eje de las ordenadas (eje OY). Por ejemplo, en el gráfico de arriba $n$ es igual a 1 porque la recta interseca con el eje Y en y=1.

Por otro lado, el término $\bm{m}$ indica la pendiente de la recta, es decir, su inclinación. Como ves en la gráfica, $m$ es igual a 2 ya que la recta sube 2 unidades verticales por cada 1 unidad horizontal.

Evidentemente, si la pendiente es positiva la función es creciente (va hacia arriba), en cambio, si la pendiente es negativa la función es decreciente (va hacia abajo).

Calcular la pendiente de una recta

Una vez sabemos exactamente qué es la pendiente de una recta, veamos cómo se calcula. Así pues, existen 3 maneras distintas para determinar numéricamente la pendiente de una recta:

Dados dos puntos diferentes de la recta $P_1(x_1,y_1)$ y $P_2(x_2,y_2),$ la pendiente de la recta es igual a:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

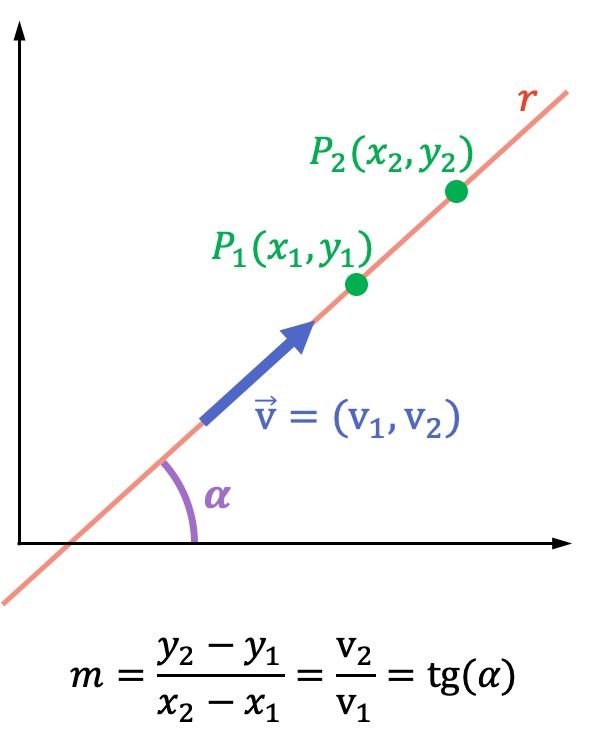
Si $\vv{\text{v}}= (\text{v}_1,\text{v}_2)$ es el vector director de la recta, su pendiente es:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Si $\alpha$ es el ángulo que forma la recta con el eje de las abscisas (eje X), la pendiente de la recta es equivalente a la tangente de dicho ángulo:

$m = \text{tg}(\alpha )$

formula de la ecuacion explicita de la recta

Ecuación punto-pendiente de la recta

La fórmula de la ecuación punto-pendiente de la recta es:

Donde:

$m$ es la pendiente de la recta.
$P_1, P_2$ son las coordenadas de un punto que pertenece a la recta $P(P_1,P_2).$

Ecuación canónica o segmentaria de la recta

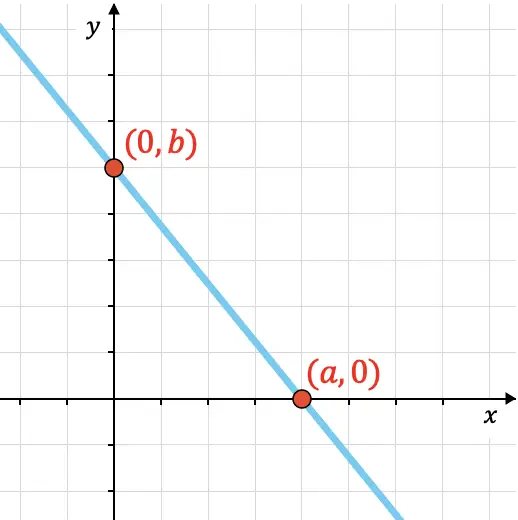
Aunque esta variante de la ecuación de la recta es menos conocida, la ecuación canónica de la recta se puede obtener a partir de los puntos de corte de la recta con los ejes cartesianos.

Sean los dos puntos de corte con los ejes de una recta determinada:

Corte con el eje X: $(a,0)$

Corte con el eje Y: $(0,b)$

La fórmula de la ecuación canónica de la recta es:

En matemáticas la ecuación canónica de la recta también se dice ecuación segmentaria o ecuación simétrica.

Por otro lado, los coeficientes $a$ y $b$ también se pueden encontrar a partir de la ecuación general de la recta mediante las siguientes fórmulas:

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

Todas las ecuaciones de la recta (fórmulas)

A modo de resumen, a continuación tienes una tabla en la que se incluyen las fórmulas de todas las ecuaciones de la recta:

Ejemplo de cómo calcular las ecuaciones de la recta

Ahora que ya hemos visto toda la explicación de la ecuación de la recta, veamos cómo se resuelve un problema típico de las ecuaciones de la recta:

Halla todas las ecuaciones de la recta que queda determinada por el punto $P$ y el vector $\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

Primero de todo, hallamos la ecuación vectorial de la recta a partir de su fórmula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Simplemente tenemos que sustituir las coordenadas del punto y del vector en la fórmula:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

En segundo lugar, encontramos las ecuaciones paramétricas de la recta mediante su correspondiente fórmula:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Y también determinamos la ecuación continua de la recta con su fórmula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

Como has podido comprobar, la ecuación vectorial, la paramétrica y la continua son fáciles de calcular, solamente hay que utilizar sus respectivas fórmulas.

Ahora pasamos a averiguar la ecuación general (o implícita) de la recta. Para ello, multiplicamos en cruz las dos fracciones de la ecuación continua:

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

Ahora podemos determinar la ecuación explícita de la recta despejando la incógnita $y$ de la ecuación implícita:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

Por lo tanto, la pendiente de la recta es igual a 2 (término que acompaña la variable independiente $x$ ).

$m=2$

Y con esto, podemos calcular la ecuación punto-pendiente de la recta con su fórmula:

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

Finalmente, para hallar la ecuación segmentaria de la recta calculamos sus puntos de intersección con los ejes OX y OY y luego aplicamos su fórmula:

$y=2x-7$

Punto de corte con el eje de las abscisas (eje X)

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

Punto de corte con el eje de las ordenadas (eje Y)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

Ecuación de la recta que pasa por dos puntos

Otro problema muy habitual de las ecuaciones de la recta es encontrar la ecuación de la recta que queda determinada por dos puntos dados. Aunque podríamos calcular el vector director de la recta con los 2 puntos y luego la ecuación, a continuación te proporcionamos una fórmula con la que podrás encontrar directamente la ecuación de dicha recta de manera fácil y rápida.

Dados dos puntos cualesquiera que pertenecen a una recta:

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

La fórmula para hallar la ecuación de la recta a partir de sus 2 puntos es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

Esta fórmula sirve para calcular directamente la ecuación punto-pendiente de la recta cuando nos dan 2 puntos por los que pasa la recta.

Ejercicios resueltos de las ecuaciones de la recta

Ejercicio 1

Halla la ecuación vectorial, las ecuaciones paramétricas y la ecuación continua de la recta que queda definida por el punto $P$ y su vector director $\vv{\text{v}}.$ Siendo ambos:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

Ver solución

En primer lugar, calculamos la ecuación vectorial de la recta a partir de su fórmula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

Luego encontramos las ecuaciones paramétricas de la recta mediante su correspondiente fórmula:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Y, por último, determinamos la ecuación continua de la recta con su respectiva fórmula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

Ejercicio 2

Calcula la ecuación implícita, la ecuación explícita y la ecuación punto-pendiente de la recta que está determinada por el punto $P$ y su vector director es $\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

Ver solución

La fórmula de la ecuación implícita de la recta es:

$Ax+By+C=0$

De forma que debemos encontrar los coeficientes A, B y C. Las incógnitas A y B se obtienen a partir de las coordenadas del vector director de la recta, porque siempre se cumple la siguiente igualdad:

$\vv{\text{v}}= (-B,A)$

Por lo tanto, el coeficiente A es la segunda coordenada del vector, y el coeficiente B es la primera coordenada del vector cambiada de signo:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

Por tanto, solo nos queda averiguar el coeficiente C. Para ello, debemos sustituir el punto que sabemos que pertenece a la recta en su ecuación:

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

De manera que la ecuación implícita, general o cartesiana de la recta es:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

Ahora podemos determinar la ecuación explícita de la recta despejando la incógnita $y$ de la ecuación implícita:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

Por lo tanto, la pendiente de la recta es igual a 3 (término de delante la variable independiente $x$ ).

$m=3$

Y, a partir del valor de la pendiente de la recta, podemos calcular la ecuación punto-pendiente de la recta con su fórmula:

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

Ejercicio 3

Determina 3 puntos de la siguiente recta, que está expresada en forma de ecuación implícita o general:

$4x+2y-8 = 0$

Ver solución

Para calcular un punto de una recta simplemente tenemos que otorgar un valor a cualquiera de las variables y, entonces, hallar el valor de la otra variable en ese punto.

Calculamos un primer punto haciendo $x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

Después hallamos un segundo punto dando otro valor a la variable $x,$ por ejemplo $x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

Y, para terminar, calculamos un tercer punto resolviendo $x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

Ejercicio 4

Encuentra todas las ecuaciones de la recta que queda definida por el punto $P$ y el vector $\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

Ver solución

Primero de todo, hallamos la ecuación vectorial de la recta a partir de su fórmula:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

En segundo lugar, encontramos las ecuaciones paramétricas de la recta mediante su correspondiente fórmula:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Y también determinamos la ecuación continua de la recta utilizando su fórmula:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

Ahora pasamos a averiguar la ecuación implícita o general de la recta. Para ello, multiplicamos en cruz las dos fracciones de la ecuación continua:

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

Ahora podemos determinar la ecuación explícita de la recta despejando la incógnita $y$ de la ecuación implícita:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

Por lo tanto, la pendiente de la recta es equivalente a -2 (término que acompaña la variable independiente $x$ ).

$m=-2$

Y con esto, podemos calcular la ecuación punto-pendiente de la recta con su fórmula:

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

Finalmente, para hallar la ecuación segmentaria de la recta calculamos los puntos de corte de la recta con los ejes OX y OY y luego usamos su fórmula:

$y=-2x+2$

Punto de corte con el eje de las abscisas (eje X)

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

Punto de corte con el eje de las ordenadas (eje Y)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

Ejercicio 5

Averigua la ecuación de la recta que pasa por los siguientes dos puntos:

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

Ver solución

Como ya sabemos dos puntos de la recta, aplicamos directamente la fórmula de la ecuación de la recta dados 2 puntos:

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

Ahora sustituimos las coordenadas cartesianas de los puntos en la fórmula:

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

Y, por último, calculamos la pendiente de la recta:

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

Así que la ecuación de la recta que pasa por esos dos puntos es:

$\bm{y+1= 3(x-4)}$

Ecuaciones de la recta

¿Cuáles son todas las ecuaciones de la recta?

Ecuación vectorial de la recta

Ecuaciones paramétricas de la recta

Ecuación continua de la recta

Ecuación implícita o general de la recta

Ecuación explícita de la recta

Significado de los parámetros m y n

Calcular la pendiente de una recta

Ecuación punto-pendiente de la recta

Ecuación canónica o segmentaria de la recta

Todas las ecuaciones de la recta (fórmulas)

Ejemplo de cómo calcular las ecuaciones de la recta

Ecuación de la recta que pasa por dos puntos

Ejercicios resueltos de las ecuaciones de la recta

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Deja un comentario Cancelar respuesta