En esta página encontrarás qué significa que dos rectas sean coplanarias. También podrás ver cuándo dos rectas son coplanarias y, además, hallarás ejemplos y ejercicios resueltos de rectas coplanarias.
Índice
¿Qué son dos rectas coplanarias?
En geometría analítica, la definición de rectas coplanarias es la siguiente:
Dos rectas son coplanarias cuando se encuentran en el mismo plano. Por lo tanto, las rectas coplanarias solo pueden ser rectas secantes, rectas paralelas o rectas coincidentes.
Además, dos rectas coplanarias son suficientes para definir completamente un plano. Aunque, evidentemente, un plano puede tener más de dos rectas coplanares, de hecho, cualquier plano contiene infinitas rectas.
Por otro lado, si dos rectas no son coplanarias significa que son rectas que se cruzan.
Ejemplos de rectas coplanarias
Para que puedas entender mejor el concepto de rectas coplanarias, a continuación tienes un ejemplo con tres rectas:
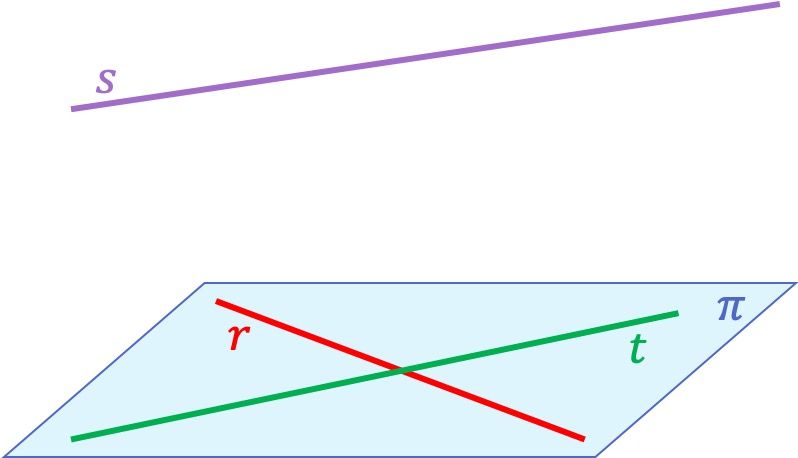
En este caso las rectas y
son coplanarias porque pertenecen al mismo plano. En cambio, la recta
no es coplanaria con ninguna de las otras dos rectas, ya que se cruza con las rectas
y
¿Cómo saber si dos rectas son coplanarias?
Como hemos visto arriba en la explicación de las rectas coplanarias, estas solamente pueden rectas secantes, paralelas o coincidentes. Es decir, 2 rectas cruzadas nunca serán coplanarias.
Por lo tanto, para hallar si dos rectas son coplanarias se tiene que determinar la posición relativa entre ellas, y si se trata de dos rectas secantes, paralelas o coincidentes, quiere decir que son rectas coplanarias.
De manera que para poder comprobar la coplanaridad de dos rectas, debes saber primero cómo calcular la posición relativa de dos rectas en el espacio. Si aún no dominas este concepto, es mejor que primero le eches un vistazo al enlace, donde encontrarás toda la explicación junto con ejemplos, ejercicios y problemas resueltos.
Ejercicio resuelto de rectas coplanarias
A modo de ejemplo, vamos a resolver un ejercicio típico sobre rectas coplanarias:
- Halla si las siguientes dos rectas son coplanarias o no:
Lo primero que debemos hacer es hallar la posición relativa entre las dos rectas y, para ello, debemos tener ambas expresadas con el mismo tipo de ecuación. Así que pasaremos la recta de ecuación general (o implícita) a ecuaciones paramétricas:
De modo que el vector director de cada recta es:
Las coordenadas de los vectores directores de las dos rectas son proporcionales, por lo que solo pueden ser rectas coincidentes o paralelas. Por tanto, en este caso en particular, no es necesario calcular la posición relativa exacta, ya que tanto las rectas paralelas como las rectas coincidentes son rectas coplanarias. Así que las dos rectas son coplanarias.
