▷ Cómo hallar la ecuación de la Elipse (fórmula y ejemplos)

Aquí encontrarás cómo se calcula la ecuación de la elipse (fórmula), tenga el origen como centro o no. También hallarás cuáles son los elementos de la elipse, cómo calcularlos y para qué sirven. Además, podrás ver ejemplos y ejercicios resueltos de ecuaciones de elipses.

Índice

Fórmula de la ecuación de la elipse

La fórmula de la ecuación de la elipse en coordenadas cartesianas es la siguiente:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

Donde:

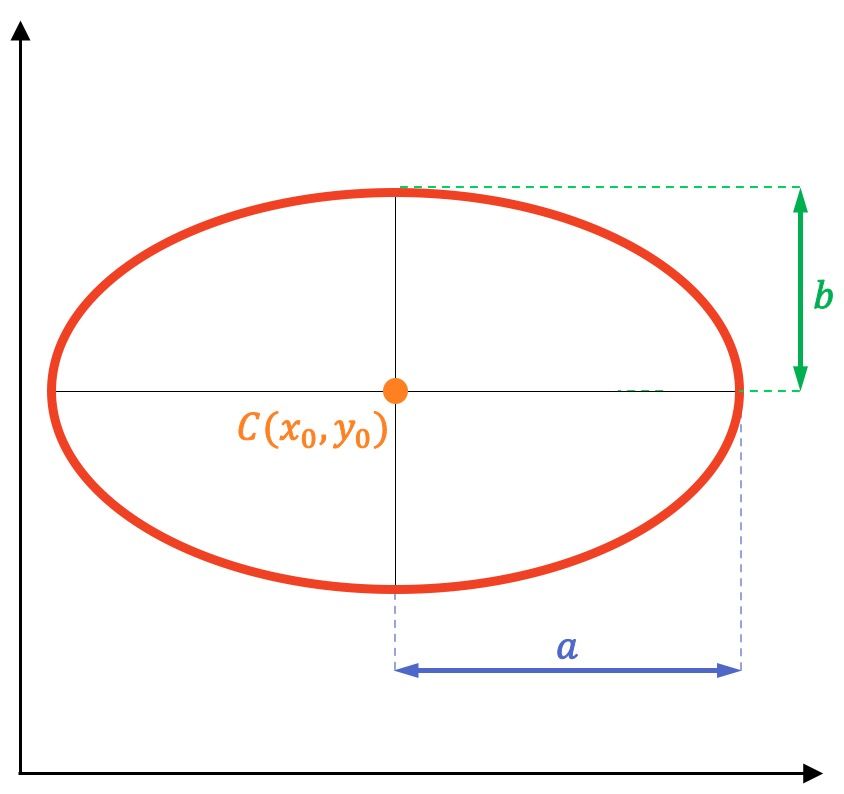
$x_0$ y $y_0$ son las coordenadas del centro de la elipse: $C(x_0,y_0)$
$a$ es el radio horizontal de la elipse.
$b$ es el radio vertical de la elipse.

Ecuación de la elipse centrada en el origen

Un tipo de elipse muy habitual es la que tiene su centro en el origen de coordenadas, es decir, en el punto (0,0). Por eso vamos a ver cómo hallar la ecuación de la elipse centrada en el origen.

Siguiendo la fórmula de la ecuación de la elipse:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

Si la elipse está centrada en el origen de coordenadas significa que $x_0$ e $y_0$ son iguales a 0, por lo que su ecuación será:

$\cfrac{\bm{x^2}}{\bm{a^2}}+\cfrac{\bm{y^2}}{\bm{b^2}} \bm{= 1}$

Hay matemáticos que también llaman a esta expresión ecuación canónica o ecuación reducida de la elipse.

Elementos de la elipse

Una vez vista cómo es es la ecuación de la elipse, vamos a ver cuáles son sus elementos. Pero antes, recordaremos qué es exactamente una elipse:

La elipse es una línea curva, cerrada y plana muy parecida a la circunferencia, pero su forma es más ovalada. En particular, la elipse es el lugar geométrico de todos los puntos de un plano cuya suma de distancias a otros dos puntos fijos (llamados focos F y F’) es constante.

Así pues, los elementos de una elipse son:

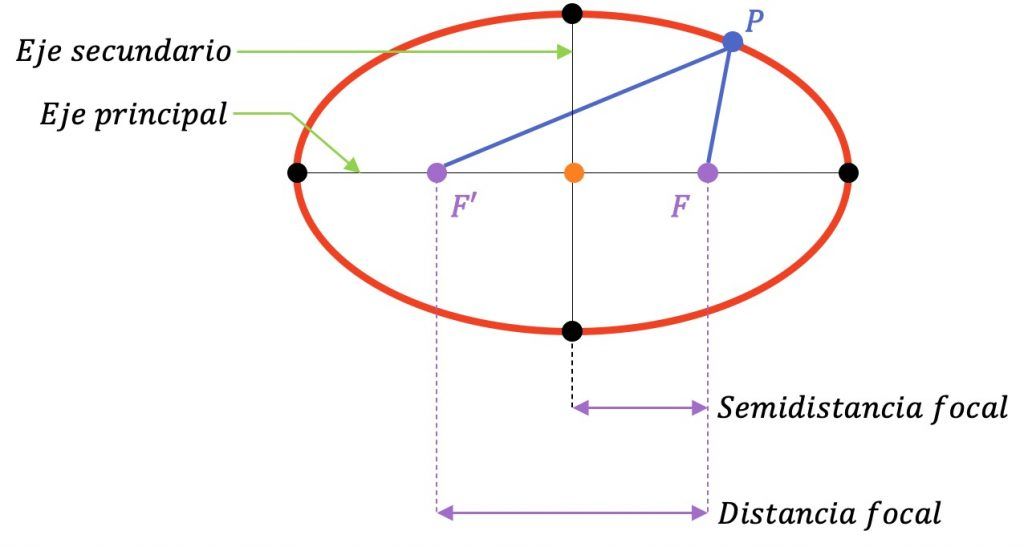
Focos: son los puntos fijos F i F’ (puntos de color lila en la imagen de abajo). La suma de las distancias desde un punto cualquiera de la elipse hasta cada foco es constante para todos los puntos de la elipse.
Eje principal o focal: es el eje de simetría de la elipse en el que se encuentran los focos. También se denomina eje mayor.
Eje secundario: es el eje de simetría de la elipse perpendicular al eje principal. También se dice eje menor y corresponde a la mediatriz del segmento que une los focos.
Centro: es el punto donde se cortan los ejes de la elipse. Además, es el centro de simetría de la elipse (punto de color naranja en el gráfico).
Vértices: puntos de intersección de la elipse con sus ejes de simetría (puntos de color negro).
Semieje mayor o principal: segmento que va desde el centro de la elipse hasta los vértices del eje principal.
Semieje menor o secundario: segmento entre el centro de la elipse y los vértices del eje secundario.
Distancia focal: se trata de la distancia entre los dos focos.
Semidistancia focal: corresponde a la distancia que hay entre el centro y cada uno de los focos.
Radio vectores: son los segmentos que unen un punto cualquiera de la elipse con cada foco (segmentos de color azul en la gráfica).

Relación entre los elementos de una elipse

Los diferentes elementos de una elipse están relacionados entre sí. Además, las relaciones que hay entre ellos son muy importantes para los ejercicios de elipses, ya que se suelen necesitar para resolver los problemas de elipses y determinar sus ecuaciones.

Como hemos visto más arriba en la definición de la elipse, la distancia de cualquier punto de la elipse al foco F más la distancia del mismo punto al foco F’ es constante. Pues ese valor constante es igual al doble de lo que mide el semieje mayor. O dicho de otra forma, la siguiente igualdad se cumple para cualquier punto de una elipse:

$d(P,F) + d(P,F')= 2a$

Donde $d(P,F)$ y $d(P,F')$ es la distancia del punto P al foco F y F’ respectivamente y $a$ es la longitud del semieje focal.

Por lo tanto, como el vértice del eje secundario está justo en la mitad del eje focal, la distancia desde este hasta uno de los focos es equivalente a la longitud del semieje principal ( $a$ ):

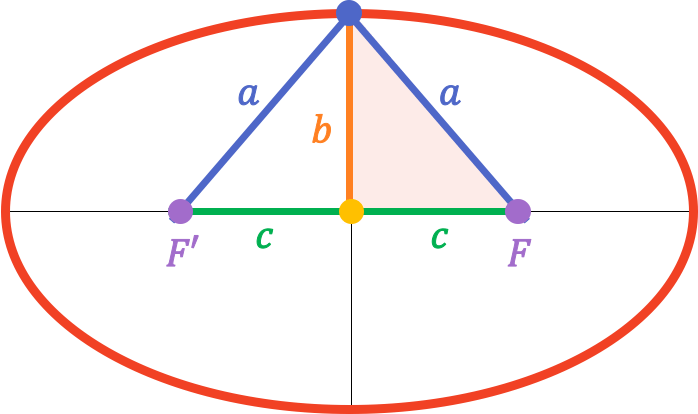
Por tanto, a partir del teorema de Pitágoras, se puede encontrar la relación que existe entre el semieje principal, el semieje secundario y la semidistancia focal:

$a^2=b^2+c^2$

Recuerda esta fórmula porque te será muy útil para calcular el resultado de los ejercicios con elipses.

Excentricidad de la elipse

Evidentemente, no todas las elipses son iguales, sino que unas son más alargadas y otras más achatadas. Así pues, existe un coeficiente que sirve para medir cuánto redondeada está una determinada elipse. Este coeficiente se llama excentricidad y se calcula con la siguiente fórmula:

$e = \cfrac{c}{a}$

Donde $c$ es la distancia del centro de la elipse a uno de sus focos y $a$ la longitud del semieje principal.

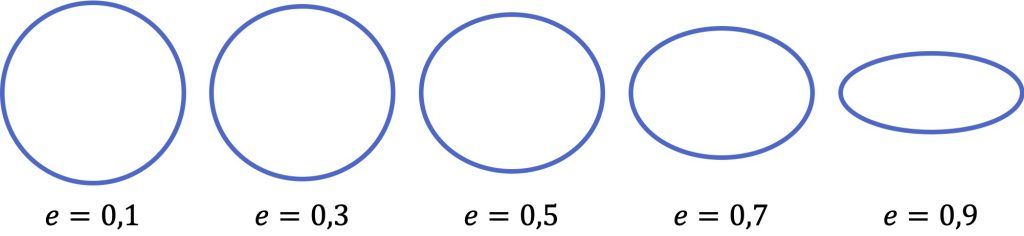
Como puedes ver en la representación anterior, cuanto más pequeño es el valor de la excentricidad de la elipse más se parece a una circunferencia, por contra, cuanto más grande es el coeficiente más aplanada es la elipse. Además, el valor de la excentricidad va desde cero (circunferencia perfecta) hasta uno (línea horizontal), ambos no incluidos.

$0<e<1$

Ejemplo de cómo calcular la ecuación de la elipse

Una vez hemos visto todas las propiedades de la elipse, vamos a resolver un problema de elipse a modo de ejemplo:

Halla la ecuación de la elipse cuyo semieje principal mide 5 unidades (y es paralelo al eje OX), su centro es el punto C(4,-1) y la distancia desde su centro hasta un foco es de 4 unidades.

Para determinar la ecuación de cualquier elipse necesitamos la longitud del semieje principal, la longitud del semieje secundario y las coordenadas de su punto. Por tanto, en este caso solo nos falta por conocer el semieje secundario.

Así pues, para calcular cuánto mide el semieje secundario, podemos usar la relación entre el semieje principal, el semieje secundario y la semidistancia focal:

$a^2=b^2+c^2$

$b^2=a^2-c^2$

$b=\sqrt{a^2-c^2} = \sqrt{5^2-4^2}=\sqrt{9} = 3$

Y una vez sabemos la longitud de los dos semiejes y su centro, podemos hallar la ecuación de la elipse mediante su fórmula:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

$\cfrac{(x-4)^2}{5^2}+\cfrac{(y-(-1))^2}{3^2} = 1$

$\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\bm{(y+1)^2}}{\bm{9}} \bm{= 1}$

Ejercicios resueltos de la ecuación de la elipse

Ejercicio 1

¿Cuál es la ecuación de la elipse centrada en el punto C(2,0) cuyo semieje principal (paralelo al eje X) y eje secundario miden 6 y 3 unidades respectivamente? Representa gráficamente dicha elipse.

Ver solución

La ecuación de la elipse es de la siguiente forma:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

Por tanto, a partir de los datos del enunciado, podemos completar la ecuación de la elipse:

$\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1$

$\cfrac{\bm{(x-2)^2}}{\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}$

Y una vez sabemos la ecuación de la elipse, podemos graficar la figura:

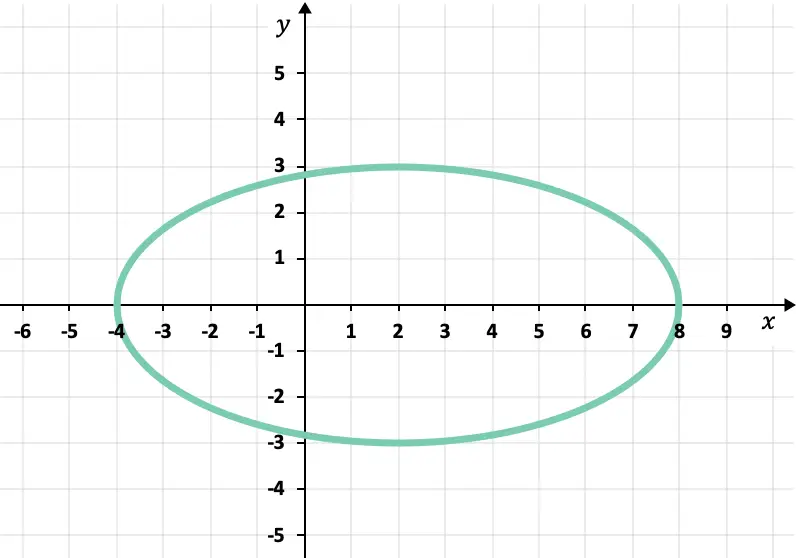
ecuacion de la elipse con el centro fuera del origen

Ejercicio 2

Calcula la ecuación de la elipse cuyo semieje principal (paralelo al eje de las abscisas) mide 13 unidades, su centro es el origen de coordenadas y la distancia desde su centro hasta uno de sus focos es de 5 unidades.

Ver solución

Para calcular la ecuación de la elipse debemos saber cuánto mide el semieje secundario. Y, para ello, podemos usar la relación matemática que existe entre el semieje principal, el semieje secundario y la semidistancia focal:

$a^2=b^2+c^2$

$b^2=a^2-c^2$

$b=\sqrt{a^2-c^2} = \sqrt{13^2-5^2}=\sqrt{144} = 12$

Y una vez sabemos la longitud de los dos semiejes y su centro, podemos hallar la ecuación de la elipse a través de su fórmula:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

$\cfrac{(x-0)^2}{13^2}+\cfrac{(y-0)^2}{12^2} = 1$

$\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}}{\bm{144}} \bm{= 1}$

Ejercicio 3

Determina la ecuación de la siguiente elipse y las coordenadas de sus focos:

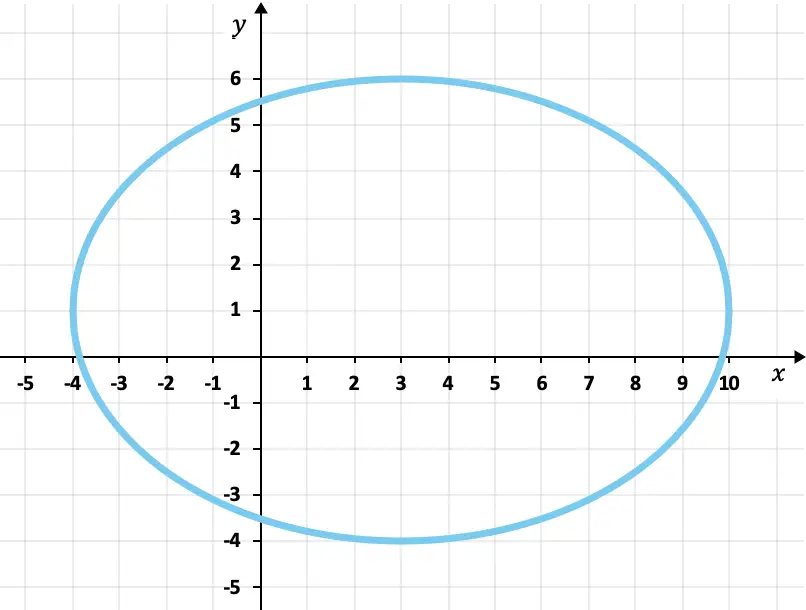
ejercicios resueltos paso a paso de ecuaciones de elipses

Ver solución

Los vértices horizontales de la elipse son los puntos (-4,1) y (10,1). Por tanto, su diámetro y su radio horizontales son:

$d_h=10-(-4) =14$

$a =\cfrac{14}{2} = 7$

Del mismo modo, los vértices verticales de la elipse son los puntos (3,6) y (3,-4). Por tanto, su diámetro y su radio verticales son:

$d_v=6-(-4) =10$

$b =\cfrac{10}{2} = 5$

De manera que solo nos falta hallar las coordenadas del centro de la elipse, que corresponden a los puntos medios de los extremos de la elipse:

$C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3$

$C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{2} = 1$

$C(3,1)$

Finalmente, la ecuación de la elipse es:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

$\cfrac{(x-3)^2}{7^2}+\cfrac{(y-1)^2}{5^2} =1$

$\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{(y-1)^2}}{\bm{25}} \bm{= 1}$

Por otro lado, la semidistancia focal es:

$a^2=b^2+c^2$

$c^2=a^2-b^2$

$c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt{24}$

Esto significa que los focos de la elipse están situados a un a distancia horizontal de $\sqrt{24}$ unidades del centro de la elipse, por lo que las coordenadas de los focos son:

$C(3,1)$

$\bm{F\left(3+\sqrt{24},1}\right)}$

$\bm{F\left(3-\sqrt{24},1}\right)}$

Ejercicio 4

Calcula la ecuación de la elipse que cumple con las siguientes características:

Su centro es el origen de coordenadas del plano cartesiano.
Su distancia focal es igual a 6 unidades.
Un punto de la elipse dista de sus focos 3 y 5 unidades.

Ver solución

Podemos calcular la semidistancia focal a partir de la distancia focal:

$2c = 6$

$c=\cfrac{6}{2}$

$c=3$

Por otra parte, sabemos por la definición de la elipse que la suma de las distancias de cualquiera de sus puntos a sus focos es equivalente a la longitud de su eje principal, por tanto:

$d(P,F) + d(P,F')= 2a$

$3+5= 2a$

$8= 2a$

$\cfrac{8}{2}= a$

$4= a$

En consecuencia, la longitud del semieje secundario de la elipse es:

$a^2=b^2+c^2$

$b^2=a^2-c^2$

$b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt{7}$

Y, en conclusión, la ecuación de la elipse es:

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

$\cfrac{(x-0)^2}{4^2}+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1$

$\cfrac{\bm{x^2}}{\bm{16}}+\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$

Finalmente, si te ha sido útil este artículo seguramente también te interesen nuestras páginas de la fórmula de la hipérbola y la fórmula de la parábola. En ellas encontrarás una explicación detallada de qué es la hipérbola y la parábola, sus ecuaciones, sus características, ejemplos, ejercicios resueltos,…

Fórmula de la ecuación de la elipse

Ecuación de la elipse centrada en el origen

Elementos de la elipse

Relación entre los elementos de una elipse

Excentricidad de la elipse

Ejemplo de cómo calcular la ecuación de la elipse

Ejercicios resueltos de la ecuación de la elipse

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Deja un comentario Cancelar respuesta