En esta página encontrarás todos los tipos de rectas que existen, además, explicamos en qué consiste cada tipo de recta y podrás ver diferentes ejemplos.
Evidentemente, antes de empezar a ver todos los diferentes tipos de rectas, para entenderlos del todo debes saber exactamente qué es una recta. De lo contrario, te recomendamos que primero le eches un vistazo a la página del enlace, donde encontrarás la definición y ejemplos de rectas.
Índice
¿Cuáles son los diferentes tipos de rectas?
Hay muchos tipos distintos de rectas, que se pueden resumir en:
- Rectas coincidentes: rectas completamente iguales.
- Rectas paralelas: rectas que siempre mantienen una misma distancia entre sí (nunca se cortan).
- Rectas secantes: rectas que tienen un punto en común.
- Rectas perpendiculares: rectas que se cortan formando un ángulo de 90º.
- Rectas oblicuas: rectas que se cortan formando un ángulo inferior a 90º.
- Rectas cruzadas: rectas que se cruzan en el espacio.
- Rectas verticales: rectas que son paralelas al eje Y.
- Rectas horizontales: rectas que son paralelas el eje X.
Como es un concepto a veces difícil de entender, hay que destacar la diferencia entre las rectas secantes y las rectas cruzadas: el primer tipo de rectas se intersecan en un punto y por tanto siempre tienen un punto de corte, en cambio, dos rectas cruzadas nunca se cortan aunque una pasa por delante de la otra.
Rectas secantes
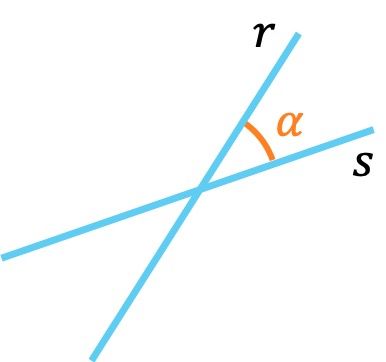
Dos rectas secantes tienen diferente dirección pero se tocan en un punto.
Rectas que se cruzan
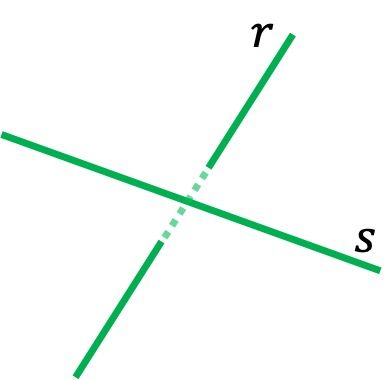
Dos rectas que se cruzan también tienen una dirección distinta, pero no se intersecan en ningún punto. Por ejemplo, en la representación gráfica de arriba la recta siempre está delante de la recta
, por lo que nunca se tocarán entre sí.
La lista de los tipos de rectas anteriores es la más conocida, pero entre ellas seguramente las rectas más utilizadas en matemáticas son las las rectas paralelas, las rectas perpendiculares y las rectas secantes. Por eso a continuación tienes un explicación más detallada de ellas.
Rectas paralelas
Las rectas paralelas son aquellas líneas que nunca se cortan, es decir, aunque se prolonguen sus trayectorias hasta el infinito nunca llegan a tocarse. Por lo tanto, los puntos de dos rectas paralelas siempre están a una misma distancia entre sí y, además, dos rectas paralelas no tienen ningún punto en común.
Por ejemplo, las siguientes dos rectas son paralelas:
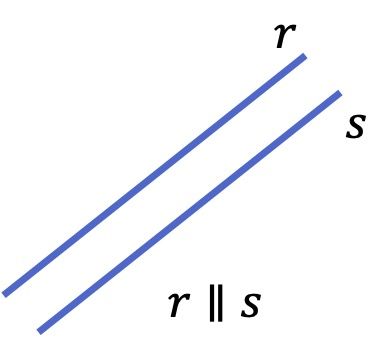
Se suele indicar que dos rectas son paralelas con 2 barras verticales || entre las rectas.
Por otro lado, a pesar de que dos rectas paralelas nunca se cortan, en geometría analítica se dice que forman un ángulo de 0º ya que tienen la misma dirección.
Si quieres profundizar más sobre este tipo de rectas puedes ver más ejemplos de rectas paralelas, además, aquí también encontrarás cuándo dos rectas son paralelas, cómo son las ecuaciones de dos rectas paralelas, sus propiedades e incluso ejercicios y problemas resueltos sobre rectas paralelas.
Rectas perpendiculares
En matemáticas, dos rectas son perpendiculares cuando se cortan en un punto formando cuatro ángulos rectos (de 90º) iguales.
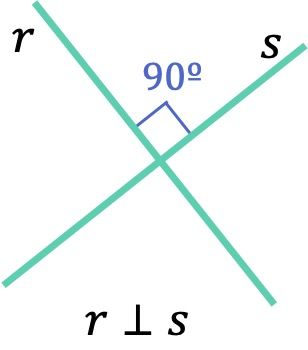
Se suele indicar la perpendicularidad de dos rectas con el símbolo
Pero para explicar el significado completo de este tipo de rectas se necesita toda una página porque realmente son muy complejas. Por esta razón hemos concentrado todo lo que debes saber sobre las rectas en un artículo nuevo: qué son las rectas perpendiculares. Aquí hallarás la explicación de cómo saber si dos (o más) rectas son perpendiculares, cómo se calcula una recta perpendicular a otra, sus propiedades, ejemplos, ejercicios resueltos y mucho más.
Rectas secantes
Dos rectas son secantes cuando se cortan únicamente en un punto. Por lo tanto, las rectas que son secantes tienen un solo punto en común.

Además, dos rectas secantes deben estar contenidas necesariamente en un mismo plano.
Al igual que antes, las rectas secantes tienen muchas características y, de hecho, algunas muy peculiares (por ejemplo las rectas perpendiculares se consideran matemáticamente un tipo de rectas secantes 😵). Por eso tenemos la página de dos rectas secantes con la explicación entera de las rectas secantes, los tipos de rectas secantes que existen, cómo se determina el punto donde se cortan, etc.
Otros tipos de rectas
Así pues, acabamos de ver los tipos de rectas más importantes en geometría, pero existen más tipos de rectas menos conocidos:
- Rectas coplanarias: dos o más rectas que pertenecen a un mismo plano.
- Rectas concurrentes: dos o más rectas que se cortan en un mismo punto y, además, están contenidas en un mismo plano.
- Recta tangente: recta que toca una curva en un único punto (llamado punto de tangencia).
- Recta de regresión: recta que sirve para aproximar la relación numérica que hay entre dos variables distintas.
- Semirrecta: cada una de las dos partes en que queda dividida una recta al cortarla por cualquiera de sus puntos.
- Segmento: fragmento de una recta que está comprendido entre dos puntos.
Evidentemente, aún existen muchísimos más tipos de rectas que no se han explicado. Debes tener en cuenta que hay tantos que no se pueden ni contar cuántos tipos de rectas hay, pero los tipos que hemos visto son los más utilizados.

buena información, me sirvió mucho, creo jeje
¡Gracias! Seguro que sí 😉
Excelente información, clara breve y precisa. Me gusto mucho. Gracias
¡Gracias a ti Wendy!
Excelente información. Gracias 👍
¡Muchas gracias Wilmer! 😉
Fue muy preciso me encanto muchísimas gracias de verdad me sirvió esa información
¡Un placer Nikol! ¡Gracias a ti por el comentario!
muchas gracias por esas informaciones
¡Gracias a ti Laura!
Muy buena información. Gracias 🙂
Gracias Rebeca 😉
a mi no me sirvió de nada 🙄😐
Lo sentimos Maria Jose, si nos dices en qué podemos mejorar lo añadiremos al post.👍
buena explicacion me sirvio demasiado
¡Gracias Elian! ¡Me alegro!
Gracias😄, Me sirvió bastante para mi tarea =D
¡Estamos para ayudarte Talys! 😉
me sirvió la información
gracias
¡Me alegro Valeria! 😀
muchisisisimas gracias que esto me ayuda a mi tarea y saque buenas notas gracias a esta información
¡Gracias 452! ¡Me alegro por ti! ¡Ahora a seguir así! 💪
Qué pasa si se modifican los valores de los coeficientes b y c en la función cuadrática
1.La parábola se convierte en una recta
2.La parábola se convierte en una hipérbola
3.La parábola sólo se traslada no cambia de forma
4.La parábola se convierte en un elipse
Hola Rene,
Resulta demasiado difícil desarrollar toda la respuesta en un solo comentario, ya que se deben entender bien las traslaciones y las transformaciones de las funciones.
Por eso te recomiendo que vayas a la página funciones.xyz donde explicamos al detalle todos los conceptos relacionados con las funciones.
Hola. Muy útil la información.
Quería saber cómo podría citar este sitio, ya que no cuenta con autor ni fecha.
De antemano, muchas gracias!
Hola Cristal,
Para citar este sitio lo importante es que pongas un enlace al artículo que has utilizado para tu trabajo.
No tiene ni fecha ni autor porque el contenido se va actualizando, por eso se suele recomendar poner la fecha en que visitaste el artículo al hacer la referencia.
¡Muchas gracias por la referencia!
me sirvió mucho GRACIAS
¡Un placer DiegoGames!