Posición relativa de dos rectas en el espacio

Aquí encontrarás todas las posiciones relativas de dos rectas en el espacio (en R3). Además, se explica cómo hallar la posición relativa entre dos rectas mediante los 2 métodos posibles: por rangos o a partir de un punto y un vector de cada recta. Incluso podrás ver ejemplos y ejercicios resueltos paso a paso.

¿Cuáles son las posiciones relativas de dos rectas en el espacio?

En geometría analítica, cuando trabajamos en un espacio tridimensional (en R3) existen 4 posibles posiciones relativas entre dos rectas: dos rectas pueden ser rectas coincidentes, rectas paralelas, rectas secantes o rectas que se cruzan.

Rectas paralelas

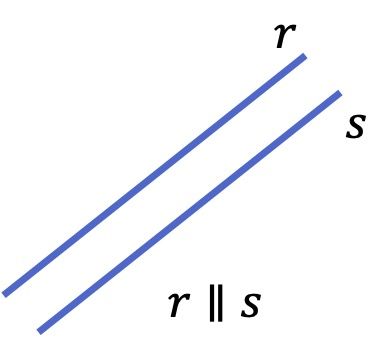
posicion relativa de dos rectas paralelas

Dos rectas son paralelas si tienen la misma dirección pero no tienen ningún punto en común. A parte, las rectas paralelas siempre están a una misma distancia entre sí.

Rectas coincidentes

posicion relativa de dos rectas coincidentes

Dos rectas son coincidentes si tienen la misma dirección y, además, todos sus puntos son comunes.

Rectas secantes

posicion relativa de dos rectas secantes

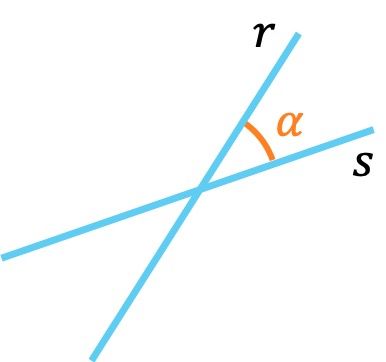
Dos rectas secantes tienen diferente dirección pero se tocan en un punto.

Rectas que se cruzan

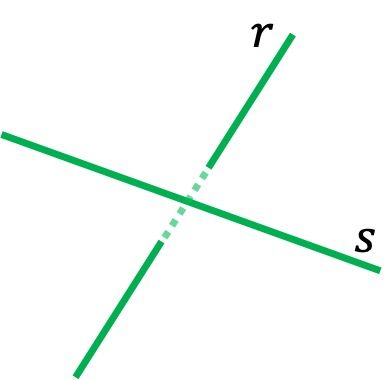
Dos rectas que se cruzan tienen distinta dirección y no se intersecan en ningún punto. Por lo tanto, dos rectas cruzadas no están en el mismo plano. Por ejemplo, en la representación gráfica de arriba la recta s siempre está delante de la recta r, por lo que nunca se tocarán entre sí.

Hay 2 maneras para saber cuál es la posición relativa entre dos rectas, ya que dependen de la forma en la que estén expresadas las ecuaciones de ambas rectas:

  • Si las rectas están en forma de ecuación vectorial, paramétrica o continua es mejor calcular la posición relativa a partir de un punto y un vector de cada recta (la explicación de este método la tienes a continuación).
  • En cambio, si las rectas están definidas en forma de ecuaciones implícitas (o generales) es más fácil averiguar la posición relativa entre las dos rectas calculando el rango de dos matrices (puedes ver la explicación más abajo).

Determinar la posición relativa de dos rectas a partir de un punto y un vector

Se puede hallar qué posición relativa hay entre dos rectas con un punto y un vector de cada recta. Este método es apropiado utilizarlo cuando las rectas están definidas en forma de ecuación vectorial, ecuaciones paramétricas o ecuación continua.

Así pues, sea el vector director y un punto cualquiera de cada una de las dos rectas:

\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}

Entonces, para hallar la posición relativa de dos rectas debemos seguir el siguiente procedimiento:

‣ Lo primero que debemos hacer es mirar si los vectores de las dos rectas son proporcionales o no y, según el caso, procedemos a hacer lo siguiente:

  • Si los dos vectores son proporcionales las rectas pueden ser paralelas o coincidentes. Por lo tanto, debemos comprobar si el punto de una recta cumple la ecuación de la otra recta:
     
    • Si el punto de una recta cumple con la ecuación de la otra recta significa que las dos rectas son coincidentes.
    • De lo contrario, implica que las dos rectas son paralelas.

  • Si los dos vectores no son proporcionales las rectas pueden ser secantes o que se cruzan. En este caso debemos resolver el siguiente determinante 3×3:

    \begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}

    • Si el determinante anterior es igual a cero, las dos rectas se cortan en un punto (son secantes).
    • Si el determinante anterior es diferente de cero, las dos rectas se cruzan.

El siguiente gráfico resume todo el procedimiento:

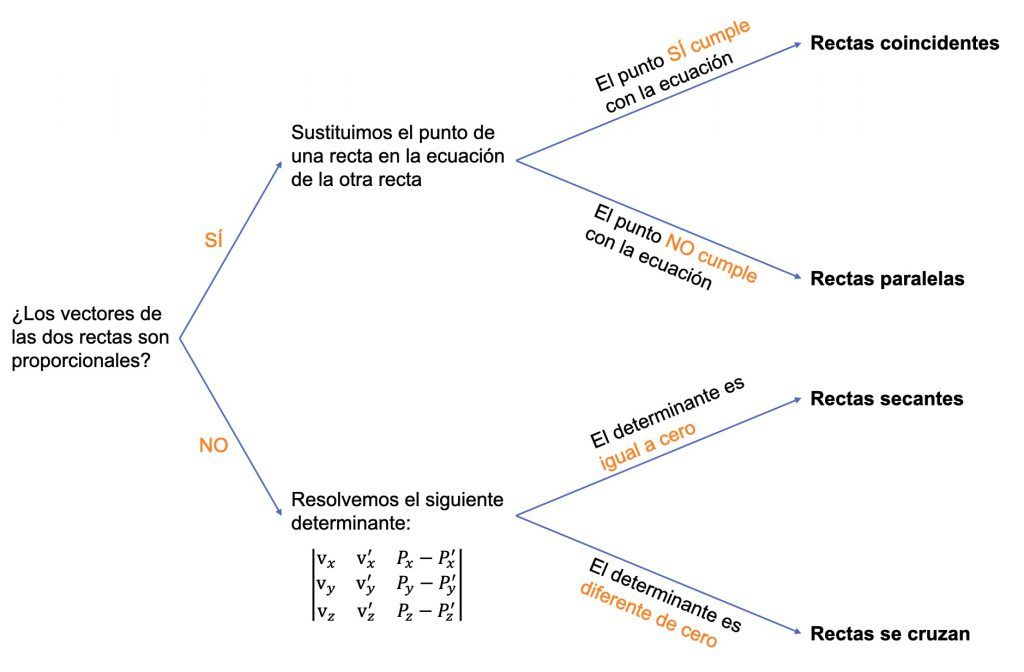
posiciones relativas de entre dos rectas

Ejemplo de cómo determinar la posición relativa entre dos rectas

El procedimiento anterior puede parecer un poco complicado, pero para que veas que es todo lo contrario vamos a resolver un problema a modo de ejemplo:

  • Determina la posición relativa entre las siguientes dos rectas:

r: \ (x,y,z)=(2,0,1)+t(4,-1,1)

s: \ (x,y,z)=(1,-3,1)+t(1,2,0)

Ambas rectas están expresadas en forma de ecuación vectorial, con lo que el vector director de cada recta es:

\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)

Y un punto por el que pasa cada recta es:

R(2,0,1)\qquad \qquad S(1,-3,1)

Una vez sabemos un punto y el vector director de cada recta, aplicamos el método visto anteriormente. En primer lugar, debemos comprobar si las coordenadas de los vectores son proporcionales:

\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}

Como los dos vectores no son proporcionales entre sí, las rectas solo pueden tocarse o cruzarse. Por tanto, ahora tenemos que resolver el siguiente determinante formado por el vector director y un punto de cada recta:

\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}

Sustituimos los valores en la fórmula:

\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}

Y calculamos el determinante, para ello puedes utilizar cualquier método (Regla de Sarrus, método de los adjuntos o cofactores, etc.):

\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1

Si el resultado del determinate hubiese sido nulo, significaría que las rectas son secantes (se tocan). Pero el determinante es distinto de 0, por tanto, las rectas se cruzan.

Hallar la posición relativa de dos rectas por rangos

Otra forma de encontrar la posición relativa de dos rectas es calculando los rangos de dos matrices concretas, como veremos a continuación. Este método es muy útil cuando ambas rectas están en forma de ecuación implícita (o general).

De manera que, si tenemos dos rectas expresadas con sus ecuaciones implícitas (o generales) en un espacio de tres dimensiones (en R3):

\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}

\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}

Sea A la matriz compuesta por los coeficientes de las dos rectas:

\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}

Y dada la matriz ampliada A’ que es la matriz formada por todos los parámetros de las dos rectas:

\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}

Entonces, la posición relativa de las dos rectas puede ser determinada por el rango de las dos matrices anteriores según la siguiente tabla:

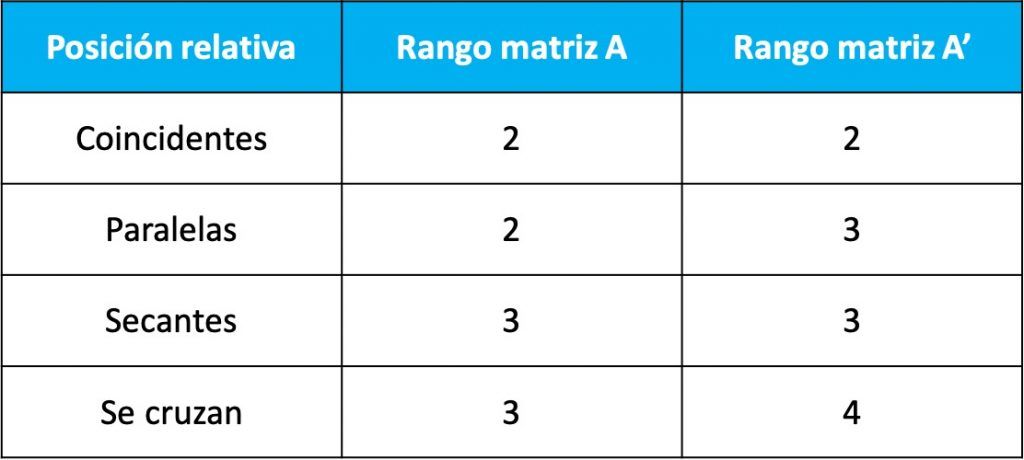
posiciones relativas de dos rectas por rangos

Por tanto, para encontrar la posición relativa entre dos rectas tendremos que calcular los rangos de las dos matrices y según el rango de cada matriz se tratará de un caso u otro.

Este teorema se puede demostrar a partir del teorema de Rouché-Frobenius (un método que sirve para resolver sistemas de ecuaciones lineales), sin embargo en esta página no haremos la demostración porque es bastante engorrosa y no aporta demasiado.

Ejemplo de cómo hallar la posición relativa de dos rectas por rangos

Una vez hemos visto la teoría sobre las posiciones relativas entre dos rectas por rangos, veamos cómo se pone en práctica mediante un ejemplo:

  • Halla la posición relativa de las siguientes dos rectas:

\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}

\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}

Las dos rectas están en forma de ecuaciones generales (o implícitas), así que usaremos el método de los rangos para encontrar la posición relativa entre las dos rectas. Por lo tanto, construimos la matriz A y la matriz ampliada A’ con los coeficientes de las rectas:

\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}

Una vez tenemos las dos matrices, tenemos que calcular el rango de cada una. Primero calculamos el rango de la matriz A por determinantes:

rg(A)= \ ?

\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}

rg(A)=3

La matriz A contiene el determinante de una submatriz 3×3 diferente de cero, por tanto, la matriz A es de rango 3.

Y ahora calculamos el rango de la matriz ampliada A’. La matriz A’ siempre será como mínimo el rango de la matriz A, que en este caso 3, de modo que solamente debemos comprobar si es de rango 4 o de rango 3. Para ello, resolvemos el determinante de la matriz 4×4 por adjuntos (o cofactores):

rg(A')= \ ?

\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =

\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}

\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50

\displaystyle =150+100-50-200

\displaystyle \bm{=0}

rg(A')=3

El determinante de toda la matriz ampliada es nulo, por lo que la matriz A’ también es de rango 3.

De manera que tanto la matriz A como la matriz A’ son de rango 3 así que, en consecuencia, las dos rectas son secantes. Es decir, solo hay un punto de corte entre ellas.

\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}

Recuerda que más arriba dispones de una tabla donde se resumen todos los posibles casos de las posiciones relativas entre dos rectas según los rangos de las matrices A y A’.

Ejercicios resueltos de la posición relativa entre dos rectas en el espacio

Ejercicio 1

Encuentra la posición relativa entre las siguientes dos rectas:

r: \ (x,y,z)=(3,4,0)+t(2,1,-3)

s: \ (x,y,z)=(1,-2,2)+t(0,5,1)

Como las dos rectas están expresadas en forma de ecuación vectorial, hallaremos la posición relativa entre las dos rectas a partir del método de un punto y un vector de cada recta.

El vector director de cada recta es:

\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)

Y un punto que pertenece a cada recta es:

R(3,4,0)\qquad \qquad S(1,-2,2)

Así pues, para aplicar el procedimiento, primero debemos verificar si las componentes de los vectores directores son proporcionales:

\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}

Como los dos vectores no son proporcionales entre sí, las rectas solo pueden ser secantes o cruzadas. Por tanto, ahora tenemos que resolver el siguiente determinante compuesto por el vector director y un punto de cada recta:

\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}

Sustituimos los valores en la fórmula:

\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}

Y calculamos el determinante:

\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0

El resultado del determinate es equivalente a 0, por tanto, las rectas son secantes.

 

Ejercicio 2

Calcula la posición relativa de las siguientes dos rectas:

\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}

La primera recta está en forma de ecuaciones paramétricas y la segunda recta en forma de ecuación continua, con lo que determinaremos la posición relativa entre las dos rectas a partir del método de un punto y un vector de cada recta.

Las coordenadas del vector director de la recta r son los coeficientes de delante del parámetro t, y las coordenadas del vector director de la recta s son los números de los denominadores:

\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)

Y un punto que pertenece a cada recta es:

R(3,1,2)\qquad \qquad S(-1,-5,4)

Así pues, para aplicar el procedimiento, primero debemos corroborar si las componentes de los vectores directores son proporcionales:

\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}

Los dos vectores son proporcionales entre sí, por lo tanto, las rectas solo pueden ser paralelas o coincidentes. Con tal de resolver esta duda, debemos sustituir el punto de la recta r en la ecuación de la recta s (o viceversa) para ver si cumple con dicha ecuación:

R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}

\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}

\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}

-1=-1 = -1

Al sustituir el punto en la recta obtenemos una igualdad, de modo que el punto de una recta cumple con la ecuación de la otra recta y, además, sus vectores directores son proporcionales. En consecuencia, las dos rectas son coincidentes.

 

Ejercicio 3

Halla la posición relativa de las siguientes dos rectas:

\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}

\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}

Las dos rectas están en forma de ecuación general (o implícita), así que utilizaremos el método de los rangos para encontrar la posición relativa entre las dos rectas. Por lo tanto, hacemos la matriz A y la matriz ampliada A’ con los coeficientes de las rectas:

\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}

Una vez tenemos las dos matrices, tenemos que calcular el rango de cada una. Primero calculamos el rango de la matriz A por determinantes:

rg(A)= \ ?

\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0

\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0

\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0

rg(A)=2

Todos los determinantes 3×3 de la matriz A son nulos, pero sí que hay un determinante 2×2 distinto de cero dentro de la matriz, de manera que la matriz A es de rango 2.

Y ahora calculamos el rango de la matriz ampliada A’. La matriz A’ siempre será como mínimo el rango de la matriz A, que en este caso 2, de modo que debemos comprobar si tiene algún determinante 3×3 que no se anule y también cuánto vale el determinate de toda la matriz:

rg(A')= \ ?

\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0

\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0

rg(A')=3

La matriz ampliada A’ sí que contiente subdeterminantes 3×3 diferentes de cero y, además, el determinante de toda la matriz ampliada es igual a 0, por lo que la matriz A’ es de rango 3.

De manera la matriz A es de rango 2 y la matriz A’ es de rango 3, por tanto, las dos rectas son paralelas. Es decir, no tienen ningún punto en común.

\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}

Recuerda que en la explicación del método (más arriba) dispones de una tabla donde se resumen todos los posibles casos de las posiciones relativas entre dos rectas según los rangos de las matrices A y A’.

 

Ejercicio 4

Averigua la posición relativa de las siguientes dos rectas:

\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}

\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}

En este caso, las dos rectas están en forma de ecuación cartesiana (o implícita), así que usaremos el método de los rangos para encontrar la posición relativa entre las dos rectas. Por lo tanto, construimos la matriz A y la matriz ampliada A’ con los coeficientes de las rectas:

\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}

Una vez conocemos las dos matrices, tenemos que calcular el rango de cada una. Primero calcularemos el rango de la matriz A por determinantes:

rg(A)= \ ?

\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}

rg(A)=3

La matriz A contiene una submatriz 3×3 cuyo determinante es diferente de cero, por tanto, la matriz A es de rango 3.

Y ahora calculamos el rango de la matriz ampliada A’. La matriz A’ siempre será como mínimo el rango de la matriz A, que en este caso 3, de modo que solamente debemos comprobar si es de rango 4 o de rango 3. Para ello, resolvemos el determinante de toda la matriz 4×4 por adjuntos (o cofactores):

rg(A')= \ ?

\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =

\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}

\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9

\displaystyle =-100-21+18

\displaystyle =-103\bm{\neq0}

rg(A')=4

El determinante de toda la matriz ampliada es diferente de cero, por lo que la matriz A’ es de rango 4.

De modo que la matriz A es de rango 3 y, por contra, la matriz A’ es de rango 4, así que las dos rectas se cruzan en un punto.

\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}

Recuerda que en la explicación del procedimiento (más arriba) tienes una tabla donde se encuentran todos los posibles casos de las posiciones relativas entre dos rectas según los rangos de las matrices A y A’.

 

4 comentarios en “Posición relativa de dos rectas en el espacio”

    1. Geometría Analítica

      Hola Mari,

      En este caso las dos rectas están definidas en un mismo plano, por tanto, simplemente debemos estudiar la proporcionalidad entre sus coeficientes.

      \cfrac{-1}{2}\neq\cfrac{1}{3}

      Los coeficientes de la x no son proporcionales a los coeficientes de la y, por lo que se trata de dos rectas secantes.

    1. Geometría Analítica

      Hola Lucia,

      Los vectores de las dos rectas no son proporcionales, por lo tanto, pueden ser secantes o cruzadas.
      \cfrac{4}{-2}=2\neq \cfrac{3}{-6}=-0,5

      De modo que para averiguar la posición relativa entre las dos rectas debemos resolver el siguiente determinante 3×3:
      \displaystyle\begin{vmatrix}4&-2&1-2\\[1.1ex] 3&-6&4-3\\[1.1ex] 2&-4&0-(-1)\end{vmatrix}=-6

      Y como el determinatnte da distinto de cero, las rectas se cruzan en el espacio.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio