En esta página encontrarás la explicación de cómo calcular el ángulo entre dos rectas (fórmula). También podrás ver varios ejemplos y, además, podrás practicar con ejercicios resueltos paso a paso.
Índice
¿Qué es el ángulo entre dos rectas?
El ángulo entre dos rectas es el ángulo más pequeño que forman esas dos rectas.
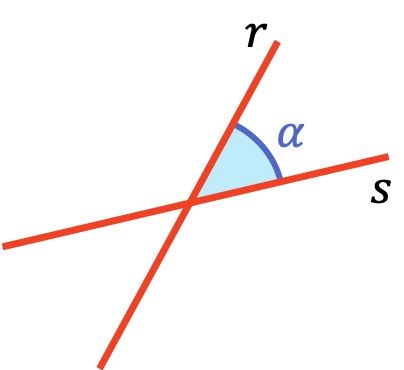
En el plano, existen cuatro tipos de rectas según el ángulo que forman entre ellas: rectas secantes (entre 0º y 90º), rectas perpendiculares (90º), rectas paralelas (0º) y rectas coincidentes (0º).
Rectas secantes
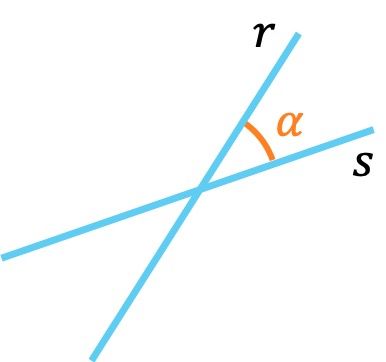
Las rectas secantes se cortan formando un ángulo agudo entre 0º y 90º.
Rectas perpendiculares
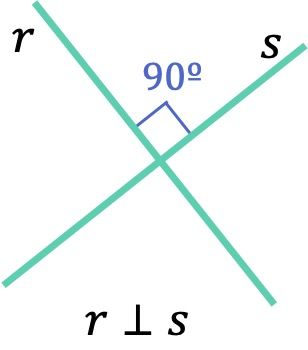
Las rectas perpendiculares se cruzan con un ángulo recto de 90º.
Rectas paralelas
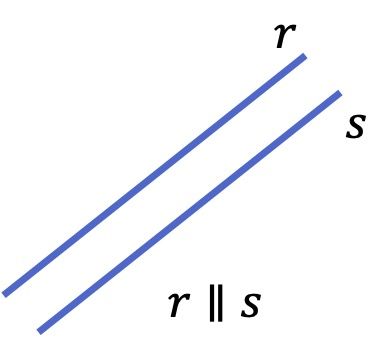
Las rectas paralelas nunca se tocan y forman un ángulo de 0º entre sí.
Rectas coincidentes

Dos rectas coincidentes tienen todos los puntos en común y, por tanto, siempre hay un ángulo de 0º entre ellas.
En conclusión, el cálculo del ángulo entre dos rectas paralelas, coincidentes o perpendiculares es inmediato: las rectas paralelas y las rectas coincidentes forman un ángulo de 0 grados ya que tienen la misma dirección, y las rectas perpendiculares se intersecan con un ángulo de 90 grados. En cambio, para hallar el ángulo entre dos rectas secantes se debe aplicar una fórmula (la veremos a continuación).
¿Cómo se calcula el ángulo entre dos rectas?
Existen dos maneras para calcular el ángulo que forman dos rectas. En el primer método se utiliza el vector director de cada recta y el segundo método se basa en la pendiente de cada recta.
Ningún procedimiento es mejor que el otro, de hecho los dos son bastante fáciles, pero dependiendo de la forma en la que estén expresadas las rectas conviene un método u otro. Así que te recomendamos saber usar los dos métodos matemáticos.
Método de los vectores directores de las rectas
La fórmula para calcular el ángulo entre dos rectas mediante sus vectores directores es la siguiente:
Dados los vectores directores de dos rectas diferentes:
El ángulo que forman estas dos rectas se puede calcular con la siguiente fórmula:
Donde y
son los módulos de los vectores
y
respectivamente.
Recordemos que la fórmula del módulo de un vector es:
Veamos cómo hallar el ángulo entre dos rectas con un ejemplo:
- Calcula el ángulo que hay entre las siguientes dos rectas:
Para calcular el ángulo que forman las dos rectas, primero debemos hallar el vector director de cada recta.
La recta está expresada en forma de ecuación paramétrica, por lo que las componentes del vector que marca su dirección son:
Y la recta está definida en forma de ecuación implícita (o general), por tanto, las coordenadas de su vector director son:
Ahora que ya sabemos el vector director de cada recta, podemos utilizar la fórmula del ángulo entre dos rectas:
Así que determinamos el módulo de los dos vectores:
Hacemos las operaciones vectoriales de la fórmula del ángulo:
Y, por último, calculamos el ángulo que forman las dos rectas con la inversa del coseno:
Recuerda que puedes calcular la inversa del coseno utilizando la calculadora con la tecla
Método de las pendientes
Evidentemente, para poder entender este método debes saber qué es la pendiente de la recta. Puedes repasar este concepto en el enlace, donde encontrarás toda una explicación al detalle de qué significa, cómo se calcula, ejemplos y ejercicios resueltos de la pendiente de una recta.
La fórmula para calcular el ángulo entre dos rectas a partir de sus pendientes es la siguiente:
Dadas dos rectas distintas:
El ángulo que forman estas dos rectas se puede determinar con la siguiente fórmula:
Donde y
son las pendientes de las rectas
y
respectivamente.
Veamos cómo calcular el ángulo entre dos rectas mediante sus pendientes con un ejemplo:
- Halla el ángulo que forman las siguientes dos rectas:
La pendiente de cada recta es el número de delante la variable
Por lo tanto, se puede hallar el ángulo entre las dos rectas aplicando la fórmula de las pendientes:
Y finalmente encontramos el ángulo con la inversa de la tangente:
Recuerda que puedes calcular la inversa de la tangente usando la calculadora con la tecla
Acabamos de ver un ejemplo con las pendientes de dos rectas expresadas en forma de ecuación explícita, pero si estuviesen en forma de ecuación punto pendiente se debería usar este mismo procedimiento.
Ejercicios resueltos de ángulos entre dos rectas
Ejercicio 1
Determina el ángulo que forman las siguientes dos rectas:
En este caso utilizaremos el método de los vectores directores. por lo tanto, primero debemos hallar el vector director de cada recta. Ambas rectas están expresadas en forma de ecuaciones paramétricas, por lo que las componentes de sus vectores directores son los términos de delante del parámetro
Ahora que ya sabemos el vector director de cada recta, podemos utilizar la fórmula del ángulo entre dos rectas:
Así que determinamos el módulo de los dos vectores:
Resolvemos el producto escalar entre los dos vectores del numerador y la multiplicación de los módulos del denominador:
Y, para acabar, hallamos el ángulo que forman las dos rectas haciendo la inversa del coseno:
Ejercicio 2
Halla el ángulo entre las siguientes dos rectas:
Resolveremos este problema utilizando el método de los vectores directores, así que primero debemos averiguar el vector director de cada recta. La recta está expresada en forma de ecuación general (o implícita), de modo que las componentes del vector que marca su dirección son:
Y la recta está definida en forma de ecuación continua, por tanto, las coordenadas cartesianas de su vector director son los números de los denominadores:
Una vez ya conocemos el vector director de cada recta, podemos utilizar la fórmula del ángulo entre dos rectas:
Así que determinamos los módulos de los dos vectores:
Hacemos las operaciones entre vectores de la fórmula del ángulo:
Y, para finalizar, calculamos el ángulo que forman las dos rectas con la inversa del coseno:
Ejercicio 3
¿Cuál es el ángulo que forman las siguientes dos rectas?
En este caso usaremos el método de las pendientes de las rectas para averiguar el ángulo que hacen, ya que las rectas están en forma de ecuación explícita.
La pendiente de cada recta es el número que acompaña la variable independiente
Por lo tanto, se puede determinar el ángulo entre las dos rectas aplicando la fórmula de las pendientes:
Y finalmente encontramos el ángulo entre las dos rectas invirtiendo la tangente:
Ejercicio 4
Encuentra la ecuación de la recta que pasa por el punto y forma un ángulo de 45º con la recta
Siendo dicha recta:
Para resolver el problema, llamaremos a la recta que vamos a calcular. Además, utilizaremos el método de las pendientes porque conocemos la pendiente de la recta
A partir de la fórmula del ángulo entre dos rectas (método de las pendientes) podemos conseguir el valor de la pendiente de la recta
Sustituimos los valores conocidos en la fórmula:
E intentamos resolver la ecuación resultante:
El valor absoluto de la ecuación dificulta un poco su resolución, porque debemos analizar tanto la opción positiva como la opción negativa:
De manera que tenemos dos posibles soluciones: una recta con pendiente -3 y otra recta con pendiente un tercio.
La fórmula de la ecuación punto-pendiente de una recta es:
Por tanto, una vez sabemos la pendiente de las dos posibles rectas, podemos escribir la ecuación punto-pendiente de cada recta con el punto por el que deben pasar según el enunciado,


Hola, buenas tardes. ¿Cómo se podría encontrar el angulo formado por estas dos rectas r: x=1+t , y=1-2t , z=1+3t s: x-1/2=y-1/-2=z-1/3 ?
Hola Valentina,
Aunque sea en un espacio de tres dimensiones, el procedimiento es el mismo.
En primer lugar debes encontrar el vector director de cada recta. La primera recta está expresada en forma de ecuación vectorial, mientras que las segunda recta está en forma de ecuación continua, por lo tanto los vectores directores son:
Luego calculamos el módulo de cada vector:
Ahora aplicamos la fórmula del ángulo entre dos vectores para hallar el coseno del ángulo que forman las rectas:
Y finalmente determinamos el ángulo invirtiendo el coseno: