Cómo calcular el módulo de un vector

En esta página verás la explicación del módulo de un vector y cómo calcularlo con su fórmula. También podrás ver cómo hallar el módulo a partir de dos puntos: su origen y su extremo. Además, encontrarás cómo determinar las componentes de un vector a partir de su módulo y las propiedades del módulo de un vector. Incluso, podrás practicar con ejemplos, ejercicios y problemas resueltos paso a paso.

Índice

¿Qué es el módulo de un vector?

El módulo de un vector representa la distancia que hay desde su origen hasta su extremo. Por lo tanto, el módulo de un vector es igual a la longitud de dicho vector.

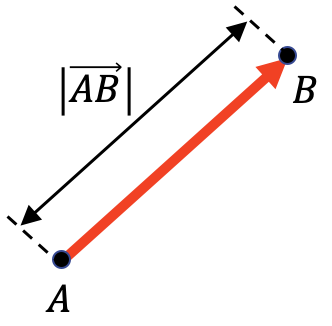
Como ves en la representación gráfica anterior, el módulo de un vector se simboliza con una barra vertical a cada lado del vector: $\lvert \vv{AB}\rvert$

Por otro lado, el módulo de un vector es lo mismo que la norma de un vector, así que quizás también lo veas escrito de esta manera. Por eso hay matemáticos que también representan el módulo de un vector con dos barras verticales a cada lado: $\lvert \lvert \vv{AB}\rvert\rvert$

Fórmula del módulo de un vector

Para hallar el módulo de un vector en el plano se debe aplicar la siguiente fórmula:

Para determinar el módulo de un vector tenemos que calcular la raíz cuadrada (positiva) de la suma de los cuadrados de sus componentes. Es decir, si tenemos el siguiente vector:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Su módulo es:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Por ejemplo, vamos a calcular el módulo del siguiente vector utilizando la fórmula:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Calcular el módulo de un vector con las coordenadas de su origen y su extremo

Acabamos de ver cómo se determina el módulo de un vector cuando sabemos sus componentes, pero ¿y si solo conocemos los puntos donde empieza y donde termina?

Entonces, para calcular el módulo de un vector a partir de las coordenadas de su origen y su extremo debemos seguir estos dos pasos:

Primero hallamos las componentes del vector. Para ello, tenemos que restar el extremo menos el origen.
Y luego calculamos el módulo del vector obtenido con la fórmula que hemos visto en el apartado anterior.

Veamos cómo se hace mediante un ejemplo:

Calcula el módulo del vector que tiene como origen el punto $A(2,1)$ y como extremo el punto $B(-1,4).$

Primero tenemos que hallar las componentes del vector, así que restamos su extremo menos su origen:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Una vez sabemos el vector, calculamos su módulo mediante la fórmula del módulo de un vector:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

Y dejamos el resultando en forma de raíz cuadrada, ya que no es exacta.

Cómo calcular las componentes de un vector a partir de su módulo

Hemos visto cómo sacar el módulo de un vector a partir de sus componentes, pero también se puede hacer el proceso inverso. Es decir, podemos calcular las componentes de un vector a través de su módulo.

El proceso que permite encontrar las componentes de un vector a partir de su módulo se denomina descomposición vectorial. Así pues, para descomponer un vector necesitamos su módulo, evidentemente, y el ángulo que forma con el eje de las abscisas (eje X).

De manera que se pueden calcular las componentes X e Y del vector con las razones trigonométricas:

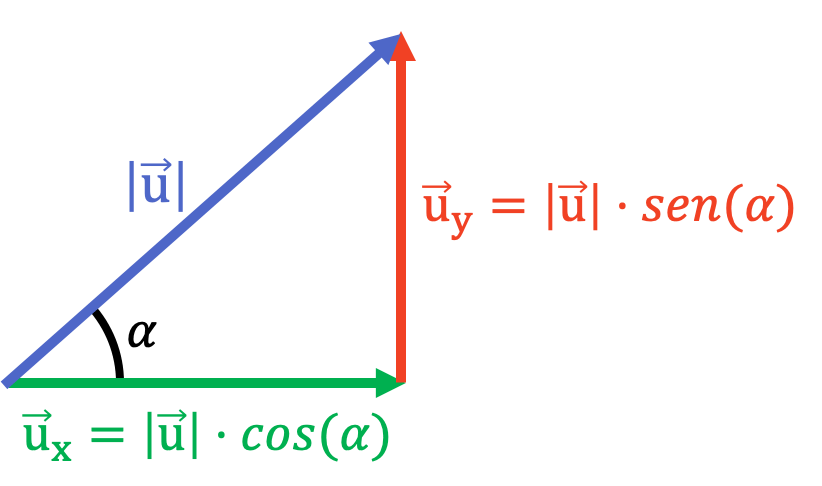
Como puedes ver en la imagen, el módulo de un vector forma un triángulo rectángulo con sus componentes, por lo que se pueden aplicar las fórmulas elementales de la trigonometría.

Hay que tener en cuenta que, a diferencia del módulo de un vector, sus componentes sí que pueden ser negativas porque el seno y el coseno pueden tomar valores negativos.

A modo de ejemplo, vamos a resolver la descomposición vectorial del vector cuyos módulo y ángulo con el eje OX son:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

La componente horizontal del vector es igual al módulo multiplicado por el coseno del ángulo:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

Y la componente vertical del vector es igual a la multiplicación del módulo por el seno del ángulo:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

De forma que el vector es el siguiente:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Propiedades del módulo de un vector

El módulo es un tipo de operación vectorial que tiene las siguientes características:

El módulo de un vector nunca puede ser negativo, siempre será igual o mayor que 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

De hecho, el único vector que existe de módulo cero es el vector nulo, es decir, el vector $\vv{\text{u}}= (0,0) .$

El módulo del producto de un vector por un número real (o un escalar) es equivalente a multiplicar el valor absoluto del escalar por el módulo del vector. Por lo tanto, se cumple la siguiente igualdad:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

Se verifica la desigualdad triangular: el módulo de la suma de dos vectores es menor o igual que la suma de sus módulos por separado.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Además, el módulo de la suma de dos vectores está relacionado con el producto escalar a través de la siguiente ecuación:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

Vector unitario

En matemáticas, un vector unitario es un vector cuyo módulo es igual a uno.

$\lvert \vv{\text{u}} \rvert=1$

Por lo tanto, la longitud de un vector unitario es una unidad.

Puede parecer muy difícil que un vector tenga como módulo exactamente 1, pero en realidad es fácil de hallar este tipo de vector:

Para hallar el vector unitario de cualquier vector simplemente tenemos que dividirlo entre su módulo:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Donde $\vv{\text{v}}_u$ es el vector unitario de $\vv{\text{v}},$ y $\lvert \vv{\text{v}} \rvert$ su módulo.

Al vector unitario también se le llama versor o vector normalizado.

Además, el vector unitario tiene la misma dirección y el mismo sentido que el vector original.

Por ejemplo, vamos a calcular el vector unitario del siguiente vector:

$\vv{\text{v}}=(1,-1)$

Para normalizar el vector primero tenemos que calcular su módulo:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

Y, finalmente, calculamos el vector unitario dividiendo el vector original entre su módulo:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Ejercicios resueltos de módulos de vectores

Ejercicio 1

Calcula el módulo del siguiente vector:

$\vv{a}=(6,8)$

Ver solución

Para calcular el módulo del vector tenemos que aplicar su fórmula:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Ejercicio 2

Ordena los siguientes vectores de menor a mayor longitud

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

Ver solución

La longitud de un vector es igual a su módulo. Por lo tanto, debemos calcular los módulos de todos los vectores:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

De modo que los vectores ordenados de menor a mayor longitud (o módulo) son:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Ejercicio 3

Determina el módulo del vector que tiene como origen el punto $A(-3,2)$ y como extremo el punto $B(7,-4).$

Ver solución

Para calcular su módulo, primer debemos hallar el vector. Para ello, restamos el extremo menos el origen:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Una vez sabemos el vector, se calcula su módulo mediante la fórmula del módulo:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Ejercicio 4

Descompone el siguiente vector y halla sus componentes:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

Ver solución

La componente horizontal del vector es igual al módulo multiplicado por el coseno del ángulo:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

Y la componente vertical del vector es igual a la multiplicación del módulo por el seno del ángulo:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

De forma que el vector es el siguiente:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

En este caso las dos componentes son idénticas, eso es debido a que el ángulo de inclinación del vector es 45º.

Ejercicio 5

Calcula el vector de misma dirección y mismo sentido que el siguiente vector pero de módulo 1.

$\vv{a} = (-4,3)$

Ver solución

El vector de misma dirección y mismo sentido pero de módulo 1 es el vector unitario. Para calcularlo primero hallamos el módulo del vector:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

Y ahora calculamos el vector unitario dividiendo el vector original entre su módulo:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

Ejercicio 6

Descompone vectorialmente el siguiente vector y calcula su vector unitario:

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

Ver solución

En primer lugar, descomponemos el vector y hallamos sus coordenadas:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

Así que el vector es el siguiente:

$\vv{a}= (5,64 \ ,\ 2,05)}$

Y ahora calculamos el vector unitario dividiendo el vector conseguido entre su módulo:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

Fíjate que las componentes de un vector unitario son iguales al coseno y al seno del ángulo que forma con el eje X.

44 comentarios en “Cómo calcular el módulo de un vector”

Naidelis Ojeda
09/02/2021 a las 15:42

(-3, 4, 1)

Responder
1. Geometría Analítica
  09/02/2021 a las 21:48
  
  Para calcular el módulo de un vector tridimensional se tiene que aplicar el mismo procedimiento que con los vectores bidimensionales. Es decir, el módulo de un vector con 3 coordenadas es igual a la raíz cuadrada (positiva) de la suma de los cuadrados de sus 3 componentes.
  
  Por tanto, el módulo del vector 3D que propones es:
  $\sqrt{(-3)^2+4^2+1^2}=\sqrt{9+16+1}=\sqrt{26}$
nathaly
22/02/2021 a las 21:51

(2,3,6)

Responder
1. Geometría Analítica
  23/02/2021 a las 10:31
  
  El módulo de un vector 3D se calcula igual que un vector 2D, por lo que debemos elevar cada una de sus coordenadas al cuadrado, sumar los resultados, y luego hacer la raíz cuadrada:
  $\sqrt{2^2+3^2+6^2}=\sqrt{49}=7$
2. Kloe
  24/06/2021 a las 23:48
  
  Determina el modulo de los siguiente vectores
  1) V=(-4,6)
  2) T=(7,5)
  3) A=(2,3)
  4) G=(7,7)
3. Geometría Analítica
  30/06/2021 a las 08:45
  
  Buenas Kloe,
  
  Te dejo el cálculo de los módulos de los vectores a continuación:
  
  $1) \ |\vv{V}|=\sqrt{(-4)^2+6^2}=\sqrt{16+36}=\sqrt{52}$
  
  $2) \ |\vv{T}|=\sqrt{7^2+5^2}=\sqrt{49+25}=\sqrt{74}$
  
  $3) \ |\vv{A}|=\sqrt{2^2+3^2}=\sqrt{4+9}=\sqrt{13}$
  
  $4) \ |\vv{G}|=\sqrt{7^2+7^2}=\sqrt{49+49}=\sqrt{98}$
saira
14/05/2021 a las 23:00

Excelente aporte me ayudó muchisimo con la tarea de mi hijo en estos tiempos. Dios lo bendiga gracias.

Responder
1. Geometría Analítica
  01/06/2021 a las 21:45
  
  ¡Me alegro Saira! ¡Cuidaros bien!
mervin
03/06/2021 a las 19:38

Halla el módulo del siguiente vector: A = (-8, 6)
por favor ayuda

Responder
1. Geometría Analítica
  05/06/2021 a las 20:55
  
  Hola Mervin,
  
  Aunque el vector tenga una componente negativa, el módulo del vector se calcula utilizando la misma fórmula:
  $|\vv{A}|=\sqrt{(-8)^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$
VICTOR MENDOZA
14/06/2021 a las 05:07

Dados los vectores A =(3,1), B =(5,-3), C =(1,2) . Calcula el módulo del vector resultante a través de la siguiente operación: 2A +B -3C

Responder
1. Geometría Analítica
  17/06/2021 a las 22:56
  
  Hola Victor,
  
  Para resolver este problema del módulo de un vector, primero debes hacer las operaciones con los vectores:
  $2\vv{A}+\vv{B}-3\vv{C}=2(3,1)+(5,-3)-3(1,2)=(6,2)+(5,-3)-(3,6)=(8,-7)$
  
  Y una vez has calculado las coordenadas del vector, ya puedes determinar el módulo aplicando la fórmula:
  $\sqrt{8^2+(-7)^2}=\sqrt{64+49}=\sqrt{113}$
Yadhira
11/08/2021 a las 00:26

Hallar la norma o modulo del vector x en la siguiente ecuación: -3(1,3) + 2x = 5(0,-2) + 4x
Ayuda

Responder
1. Geometría Analítica
  12/08/2021 a las 08:28
  
  Hola Yadhira,
  
  Para resolver este ejercicio lo primero que debemos hacer es encontrar el vector que cumple con la ecuación.
  $\begin{array}{l}-3(1,3) + 2x = 5(0,-2) + 4x \\[2ex] (-3,-9)+2x=(0,-10)+4x\\[2ex] (-3,-9)-(0,-10)=4x-2x\\[2ex] (-3,1)=2x\\[2ex] \displaystyle x=\left(\frac{-3}{2},\frac{1}{2}\right)\end{array}$
  
  Y una vez hemos calculado el vector que cumple con la ecuación, hallamos su norma utilizando la fórmula:
  $\displaystyle \sqrt{\left(\frac{-3}{2}\right)^2+\left(\frac{1}{2}\right)^2}=\sqrt{\frac{9}{4}+\frac{1}{4}}=\sqrt{\frac{10}{4}}=\sqrt{\frac{5}{2}}$
Mariapaz
24/08/2021 a las 21:45

Hallar el modulo del vector Z→=(k+1.k−1), si los vectores X→=(k+5,−4),Y→=(1,k+1) son perpendiculares

Responder
1. Geometría Analítica
  27/08/2021 a las 10:54
  
  Hola Mariapaz,
  
  Para resolver este problema, primero debemos aplicar la condición de perpendicularidad la cual dice que el producto escalar de dos vectores perpendiculares es igual a cero. De este modo podremos hallar el valor del parámetro k:
  $X \perp Y \ \longrightarrow \ X\cdot Y=0$
  
  $(k+5)\cdot 1 +(-4)\cdot (k+1)=0$
  
  $k+5-4k-4=0$
  
  $k=\cfrac{1}{3}$
  
  Ahora calculamos el vector sustituyendo el valor de la incógnita:
  $\displaystyle Z=\left(\frac{1}{3}+1,\frac{1}{3}-1\right)=\left(\frac{4}{3},-\frac{2}{3}\right)$
  
  Y, finalmente, calculamos el módulo del vector con fracciones:
  $\displaystyle |Z|=\sqrt{\left(\frac{4}{3}\right)^2+\left(\frac{2}{3}\right)^2}=\sqrt{\frac{16}{9}+\frac{4}{9}}=\sqrt{\frac{20}{9}}$
Cecilia
29/09/2021 a las 02:37

Grafica y encuentra el modulo y la dirección de los siguientes vectores.
X=8, Y=12.
X=8, Y=6.
X=10, Y=16

Responder
1. Geometría Analítica
  30/09/2021 a las 09:54
  
  Hola Cecilia, tienes resuelto el cálculo del módulo de los vectores a continuación:
  
  $\sqrt{8^2+12^2}=\sqrt{64+144}=\sqrt{208}$
  
  $\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$
  
  $\sqrt{10^2+16^2}=\sqrt{100+256}=\sqrt{356}$
  
  Para graficar los vectores puedes ver buscar cómo se hace en el buscador de esta página web.
Lenihan
30/09/2021 a las 02:57

Dado el conjunto de vectores mostrados en la figura, determinar el módulo de su
vector resultante, si A=10; B= 20; C = 6; D = 13.

Responder
1. Geometría Analítica
  30/09/2021 a las 09:57
  
  Hola Lenihan,
  
  Para poder resolver este ejercicio es necesario poder ver cómo es la figura, o al menos tener una descripción de ella.
Angelina
30/09/2021 a las 15:55

(4,6)

Responder
1. Geometría Analítica
  02/10/2021 a las 13:43
  
  Hola Angelina, el cálculo del módulo del vector que propones se hace de la siguiente manera:
  
  $\sqrt{4^2+6^2}=\sqrt{16+36}=\sqrt{52}$
Yesimar
11/10/2021 a las 18:00

Me podrían ayudar

Responder
1. Geometría Analítica
  13/10/2021 a las 12:23
  
  Sí, por supuesto Yesimar. ¿En qué necesitas ayuda?
Erismelyn
04/11/2021 a las 02:14

Me puedes ayudar
U=(-5,2)
B=(0,5)
V=(-2,-6)
V=(6,8)
La necesito para mañana pliss.😘😘

Responder
1. Geometría Analítica
  08/11/2021 a las 11:07
  
  Hola Erismelyn,
  
  Para encontrar el módulo de un vector debes elevar cada componente al cuadrado, sumar los cuadrados, y luego hacer la raíz cuadrada:
  
  $\displaystyle\begin{vmatrix}\vv{U}\end{vmatrix}=\sqrt{(-5)^2+2^2}=\sqrt{25+4}=\sqrt{29}$
  
  $\displaystyle\begin{vmatrix}\vv{B}\end{vmatrix}=\sqrt{0^2+5^2}=\sqrt{25}=5$
  
  $\displaystyle\begin{vmatrix}\vv{V}\end{vmatrix}=\sqrt{(-2)^2+(-6)^2}=\sqrt{4+36}=\sqrt{40}$
  
  $\displaystyle\begin{vmatrix}\vv{U}\end{vmatrix}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$
Ismael Torres
07/11/2021 a las 15:34

(-3,-4)

Responder
1. Geometría Analítica
  09/11/2021 a las 14:48
  
  Hola Ismael, aunque las componentes del vector sean negativas, el módulo se calcula aplicando la misma fórmula:
  
  $\sqrt{(-3)^2+(-4)^2}=\sqrt{9+16}=\sqrt{25}=5$
Manuel De Los
10/11/2021 a las 02:12

Dos Vectores F1= (500 newton) 30 grados con la horizontal
F2 = (1500 newton) 70 grados con la horizontal
(a) encuentre el modulo y el Angulo del vector resultante con respecto al
eje (X) positivo Use ley del coseno y la ley de los senos método analítico

Responder
1. Geometría Analítica
  11/11/2021 a las 10:40
  
  Hola Manuel,
  
  ¿Podrías decir qué operación se hace entre los vectores? (suma, resta o multiplicación)
  
  Luego estaré encantado de poderte ayudar. 🙂
Alma Saldivar
14/11/2021 a las 17:57

Determinar el módulo y la dirección de los siguientes vectores. Representar gráficamente.
a) A (3, 4)
b) P (6, 4)
c) W (2, 8)

Responder
1. Geometría Analítica
  15/11/2021 a las 10:53
  
  Hola Alma,
  
  La dirección da cada módulo te la dan sus dos componentes y para representarlos puedes ver cómo se hace en el post correspondiente de geometriaanalitica.info.
  
  Por otro lado, el módulo de cada vector es:
  
  $|\vv{A}|=\sqrt{3^2+4^2}=\sqrt{25}=5$
  
  $|\vv{P}|=\sqrt{6^2+4^2}=\sqrt{52}$
  
  $|\vv{W}|=\sqrt{2^2+8^2}=\sqrt{68}$
Alma Saldivar
14/11/2021 a las 17:58

Sean los vectores: A (3, -1), B (-2, -2), C (½, 3/2) y D (-√5/2, √6/3 ). Calcular las siguientes sumas y restas:
A + B
A + 2C
A +D
C – B

Responder
1. Geometría Analítica
  15/11/2021 a las 11:00
  
  Hola Alma,
  
  Para sumar (o restar) dos vectores debes sumar (o restar) sus componentes:
  
  $A+B=(3,-1)+(-2,-2)=(1,-3)$
  
  $\displaystyle A+2C=(3,-1)+2\cdot \left(\frac{1}{2},\frac{3}{2}\right)=(3,-1)+(1,3)=(4,2)$
  
  $\displaystyle A+D=(3,-1)+\left(-\sqrt{\frac{5}{2}},\sqrt{\frac{6}{3}}\right)=\left(3-\sqrt{\frac{5}{2}},-1+\sqrt{\frac{6}{3}}\right)$
  
  $\displaystyle C-B=\left(\frac{1}{2},\frac{3}{2}\right)-(-2,-2)=\left(\frac{1}{2}+2,\frac{3}{2}+2\right)=\left(\frac{5}{2},\frac{7}{2}\right)$
antonio jose
07/12/2021 a las 17:59

Calcular el módulo de: A= (4,3,0)

Responder
1. Geometría Analítica
  10/12/2021 a las 19:35
  
  Hola Antonio, en este caso el vector tiene tres coordenadas, por lo que debemos aplicar la fórmula del módulo de un vector tridimensional:
  $|\vv{A}|=\sqrt{4^2+3^2+0^2}=\sqrt{25}=5$
Emma
23/12/2021 a las 06:10

Hola, necesito ayuda.
Dado los vectores
A=(5,-2,6) y B=(8,-5,-4)
Calcular
A+B, A-B, 3A y -5B

Responder
1. Geometría Analítica
  26/12/2021 a las 11:11
  
  Hola Emma,
  
  Aunque los vectores tengan tres componentes, las operaciones entre vectores se hacen de la misma manera:
  
  $\vv{A}+\vv{B}=(5,-2,6)+(8,-5,-4)=(4+8,-2+(-5),6+(-4))=(12,-7,2)$
  
  $\vv{A}-\vv{B}=(5,-2,6)-(8,-5,-4)=(4-8,-2-(-5),6-(-4))=(-4,3,10)$
  
  $3\vv{A}=3\cdot (5,-2,6)=(3\cdot 5,3\cdot (-2),3\cdot 6)=(15,-6,18)$
  
  $-5\vv{B}=-5\cdot (8,-5,-4)=(-5\cdot 8,-5\cdot (-5),-5\cdot (-4))=(-40,25,20)$
Raquel Naranjo
26/01/2022 a las 06:04

Considere los vectores D= 3i-2j+5k y E=2i-2j-2k
Cual es el vector F= 2D-3E?
Ayuda porfa 🙁

Responder
1. Geometría Analítica
  01/02/2022 a las 13:51
  
  Hola Raquel,
  
  El vector resultante de la operación es el siguiente:
  
  $\begin{aligned}F&=2D-3E\\[2ex]&= 2\cdot (6i-2j+5k)-3\cdot (2i-2j-2k)\\[2ex]&= 12i-4j+10k-6i+6j+6k\\[2ex]&= 6i+2j+16k \end{aligned}$
Lupita
08/02/2022 a las 04:33

Dados los vectores U= (4,2,1) y V=(4,5,8) hallar sus módulos

Responder
1. Geometría Analítica
  15/02/2022 a las 17:54
  
  Hola Lupita,
  
  Como los vectores tienen tres componentes, debes aplicar la misma fórmula aplicada a las tres coordenadas:
  
  $|\vv{U}|=\sqrt{4^2+2^2+1^2}=\sqrt{21}$
  
  $|\vv{V}|=\sqrt{4^2+5^2+8^2}=\sqrt{105}$
Rosanna
27/02/2022 a las 23:28

ayuda por favor
Las coordenadas de dos puntos son: A(1,4) B(5,-7), hallar las componentes y el modulo del vector opuesto a AB

Responder
1. Geometría Analítica
  02/03/2022 a las 21:51
  
  Hola Rosanna,
  
  Para determinar las componentes del módulo debes restar las coordenadas de los dos puntos:
  $\vv{AB}=B-A=(5,-7)-(1,4)=(4,-11)$
  
  Y luego para encontrar el módulo dimensional debes emplear la fórmula explicada en el post:
  $|\vv{AB}|=\sqrt{4^2+(-11)^2}=\sqrt{137}$

¿Qué es el módulo de un vector?

Fórmula del módulo de un vector

Calcular el módulo de un vector con las coordenadas de su origen y su extremo

Cómo calcular las componentes de un vector a partir de su módulo

Propiedades del módulo de un vector

Vector unitario

Ejercicios resueltos de módulos de vectores

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

44 comentarios en “Cómo calcular el módulo de un vector”

Deja un comentario Cancelar respuesta