Secciones cónicas

En esta página encontrarás la definición de las secciones cónicas, por qué son tan importantes y los diferentes tipos de secciones cónicas que hay (circunferencia, elipse, hipérbola y parábola). Además, podrás ver las diferencias entre sus ecuaciones.

¿Qué son las secciones cónicas?

En geometría analítica, las secciones cónicas (o simplemente cónicas) son todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano, cuando ese plano no pasa por el vértice del cono. Existen cuatro tipos de secciones cónicas: la circunferencia, la elipse, la parábola y la hipérbola.

A continuación tienes representadas gráficamente las 4 secciones posibles que se pueden obtener a partir de cualquier cono:

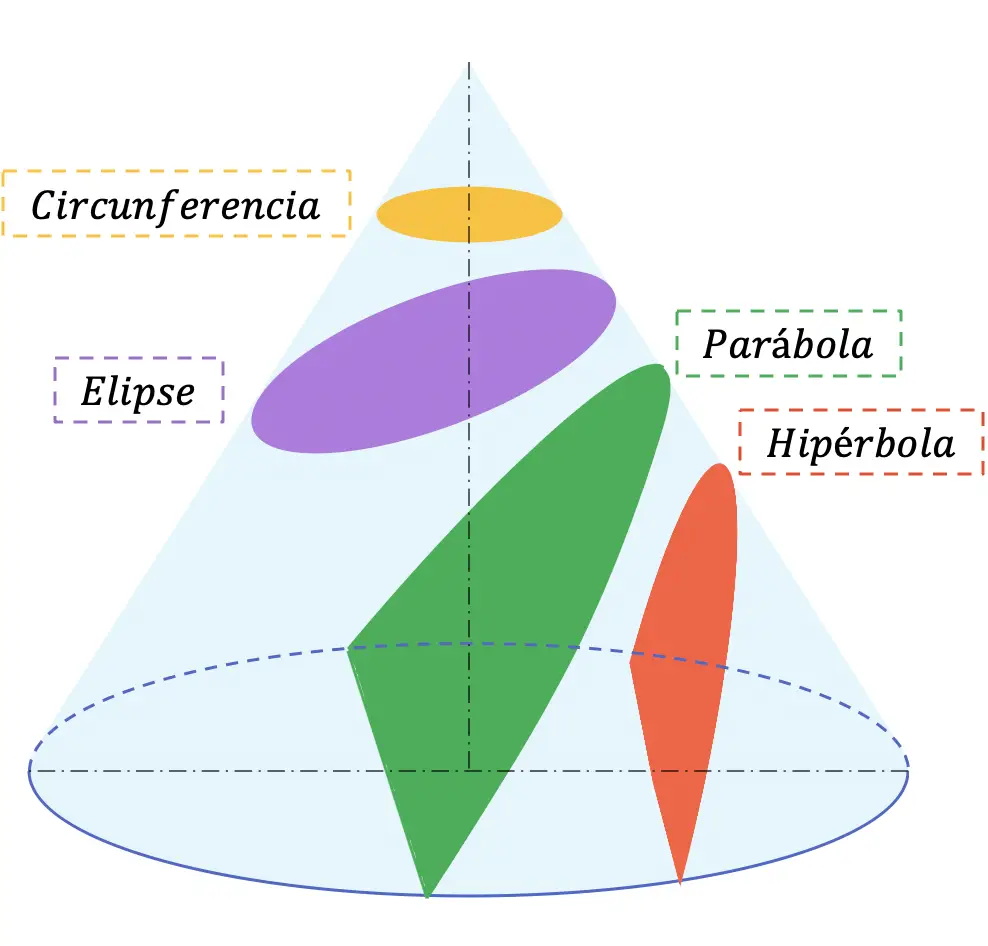
Las secciones cónicas se suelen estudiar en Secundaria (Bachillerato), en las asignaturas de matemáticas y dibujo técnico.

Tipos de secciones cónicas

Una vez visto el concepto de sección cónica, veamos cuáles son los cuatro tipos de secciones cónicas que existen: la circunferencia, la elipse, la parábola y la hipérbola.

La circunferencia

La circunferencia es una sección cónica que se puede hallar cortando un cono con un plano perpendicular a su eje de revolución (paralelo a la base).

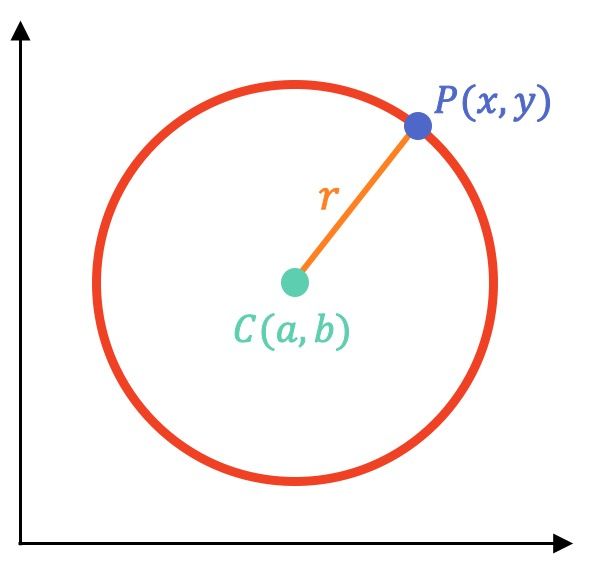
También, la circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.

Elipse

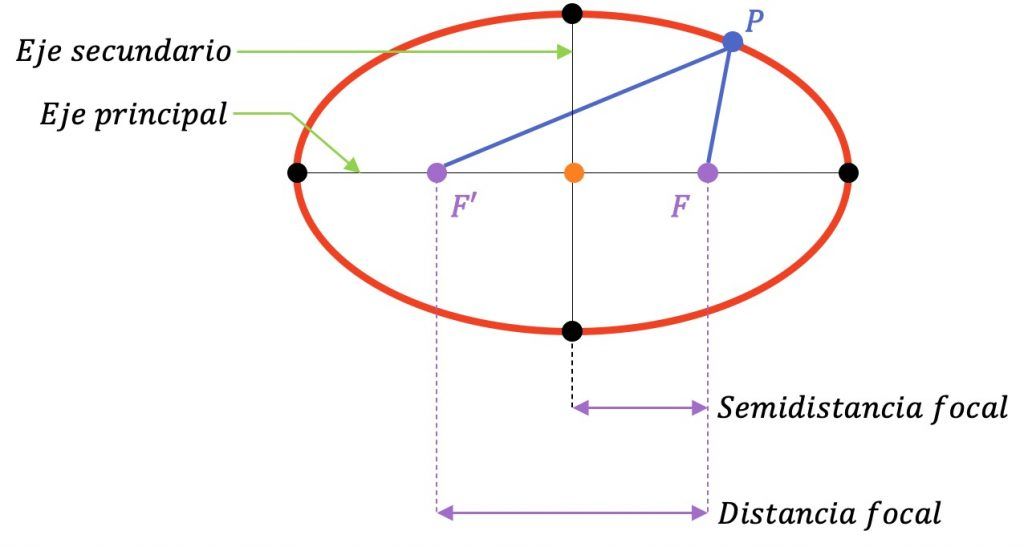
La elipse es una línea curva, cerrada y plana muy parecida a la circunferencia, pero su forma es más ovalada. En particular, es el resultado de cortar la superficie de un cono con un plano oblicuo cuyo ángulo respecto al eje de revolución es mayor que el de la generatriz.

Además, todos los puntos de una elipse cumplen con una condición: la elipse es el lugar geométrico de todos los puntos de un plano cuya suma de distancias a otros dos puntos fijos (llamados focos F y F’) es constante.

Parábola

En matemáticas, una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (llamado foco) y de una recta fija (denominada directriz).

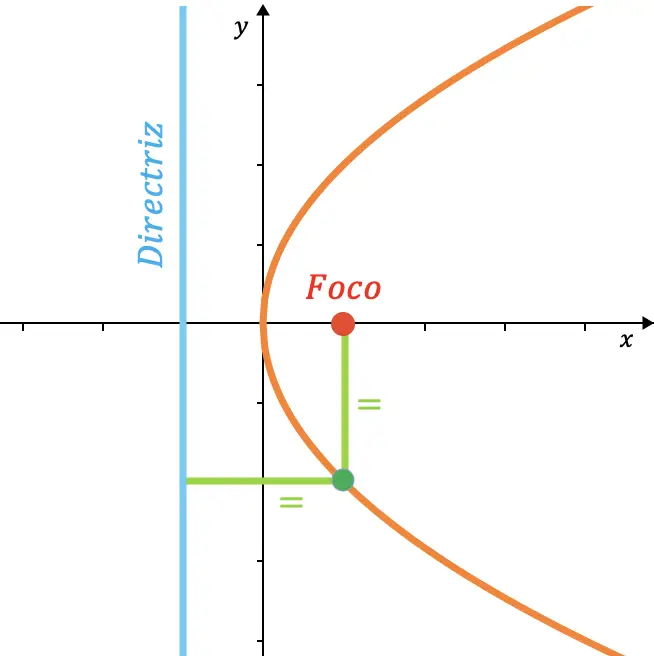
Geométricamente, la parábola es el resultado de cortar un cono con un plano con un ángulo de inclinación respecto al eje de revolución equivalente al ángulo de la generatriz del cono. Por lo tanto, el plano que contiene la parábola es paralelo a la generatriz del cono.

Una rasgo muy importante de esta sección cónica es la ecuación de la parábola, ya que según cómo sea esta permite identificar qué tipo de parábola se trata. En este enlace hallarás todas las ecuaciones de la parábola, cuáles son los elementos de la parábola, sus propiedades, ejemplos, ejercicios resueltos,… entre otras características de las parábolas.

Hipérbola

Como sección cónica, se consigue una hipérbola cuando se corta un cono mediante un plano con un ángulo menor que el ángulo que forma la generatriz del cono respecto a su eje de revolución.

Matemáticamente, una hipérbola se puede definir como el lugar geométrico de los puntos del plano que cumplen la siguiente propiedad: el valor absoluto de la diferencia de las distancias desde un punto cualquiera de la hipérbola hasta dos puntos fijos (llamados focos) debe ser constante.

Además, el valor de la resta de esas dos distancias siempre es equivalente a la distancia entre los dos vértices de la hipérbola.

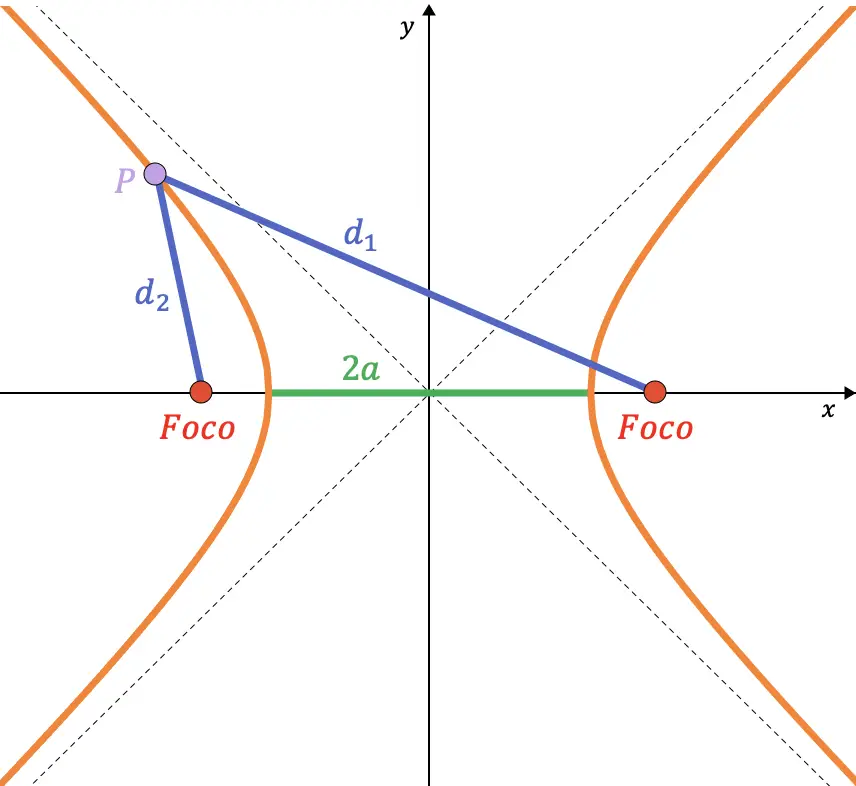
Como seguro que ya habrás deducido, el valor del parámetro  de una hipérbola es fundamental para las hipérbolas. En el siguiente enlace puedes ver nuestra explicación de la hipérbola, donde hallarás por qué es un coeficiente tan importante así como cuáles son todos los elementos que caracterizan una hipérbola. Además, encontrarás cómo es la ecuación de la hipérbola, los distintos tipos de hipérbolas que existen e, incluso, problemas y ejercicios resueltos paso a paso de hipérbolas.

Ecuación general de las secciones cónicas

Toda sección cónica se puede expresar analíticamente en forma de ecuación. De hecho, todas las ecuaciones de las secciones cónicas deben ser de segundo grado:

Por lo tanto, al menos uno de los coeficientes o de la fórmula tiene que ser diferente de cero.

De manera que en función de los valores de los parámetros la ecuación corresponderá a un tipo de sección cónica u otro:

• Circunferencia: para que la ecuación general describa a una circunferencia, los términos y deben coincidir y debe ser nulo.

• Elipse: la ecuación corresponderá a la expresión matemática de una elipse cuando se verifique la siguiente condición:

• Parábola: para que la ecuación sea de una parábola, se debe cumplir la siguiente igualdad:

• Hipérbola: finalmente, la ecuación general de una hipérbola debe satisfacer la siguiente inecuación: