Parábola (matemáticas): definición, ecuación, elementos, ejemplos,…

En esta página encontrarás todo sobre la parábola: qué es, qué representa, sus elementos (foco, directriz, vértice, etc.) su ecuación (con los diferentes tipos de ecuaciones de la parábola), ejemplos, ejercicios resueltos, sus propiedades, las aplicaciones que tiene,…

¿Qué es una parábola?

La parábola es un concepto que tiene significados muy distintos, pero su definición matemática es la siguiente:

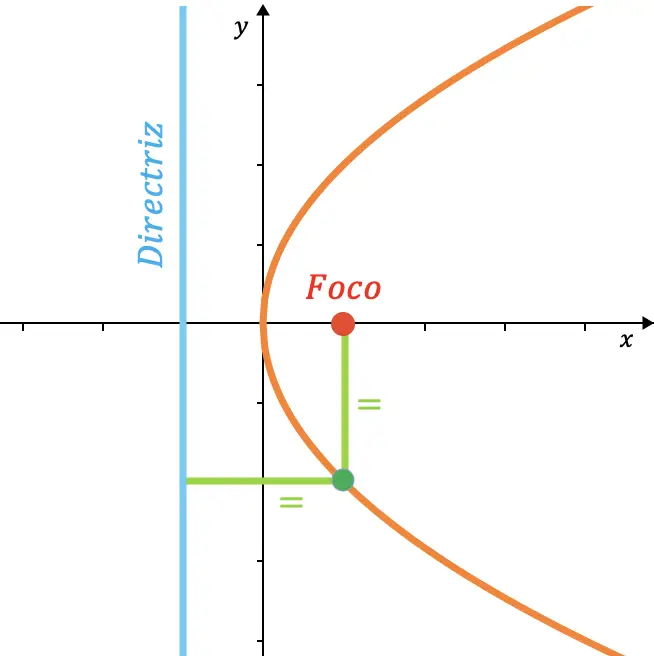
En matemáticas, una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (llamado foco) y de una recta fija (denominada directriz).

Por lo tanto, cualquier punto de una parábola esta a la misma distancia de su foco y de su directriz.

definicion de parabola
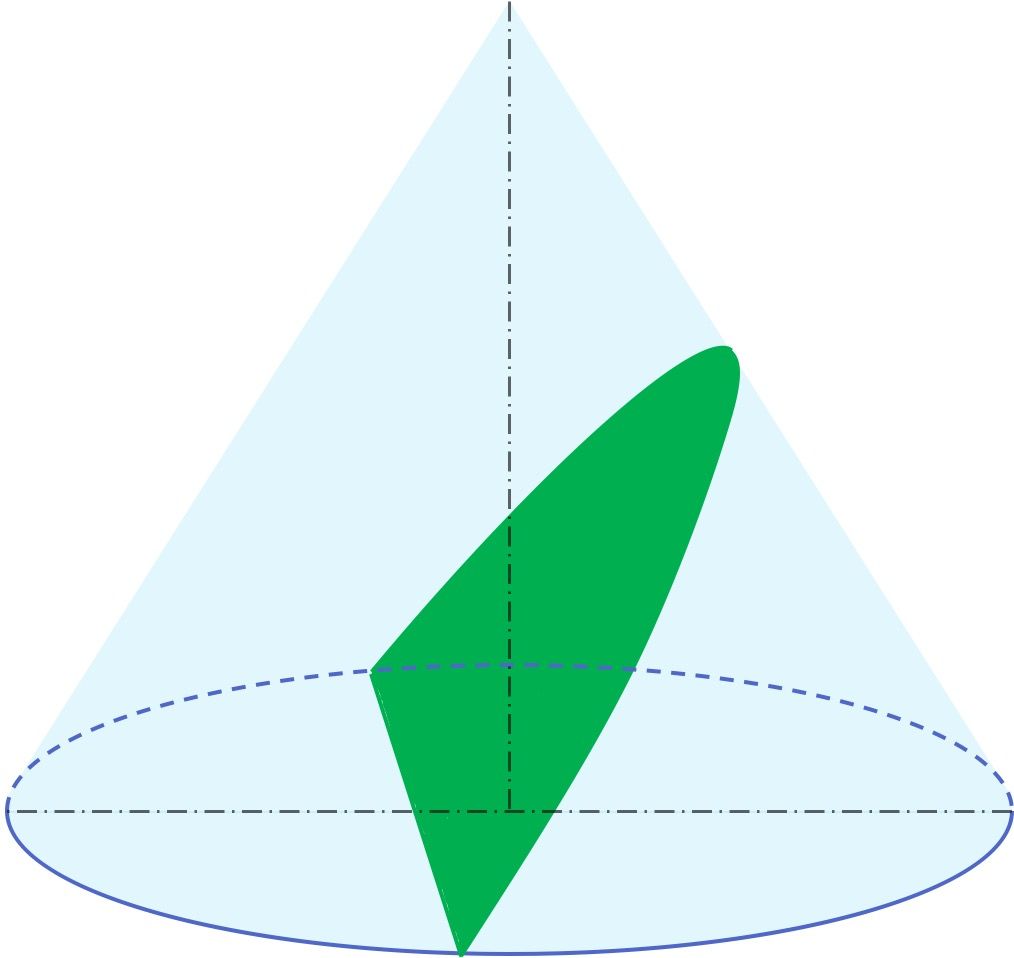
parábola sección cónica

Además, en geometría la parábola es una de las secciones cónicas junto a la circunferencia, la elipse y la hipérbola. Es decir, una parábola se puede obtener a partir de un cono.

En particular, la parábola es el resultado de cortar un cono con un plano con un ángulo de inclinación respecto al eje de revolución equivalente al ángulo de la generatriz del cono. En consecuencia, el plano que contiene la parábola es paralelo a la generatriz del cono.

Elementos de una parábola

Las características de una parábola dependen de los siguientes elementos:

  • Foco (F): es un punto fijo del interior de la parábola. La distancia de cualquier punto de la parábola al foco es igual a la distancia de ese mismo punto a la directriz de la parábola.
  • Directriz (D): es una recta fija externa a la parábola. Un punto de la parábola tiene la misma distancia a la directriz que al foco de la parábola.
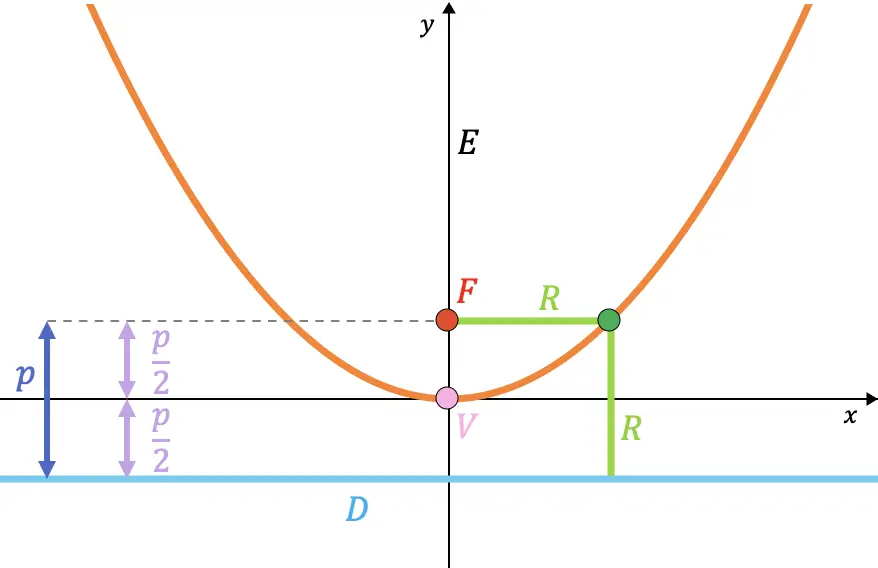
  • Parámetro (p): es la distancia desde el foco hasta la directriz.
  • Radio vector (R): es el segmento que une un punto de la parábola con el foco. Su valor coincide con la distancia del punto hasta la directriz.
  • Eje (E): es la recta perpendicular a la directriz que pasa por el foco y es el eje de simetría de la parábola, en la gráfica de abajo corresponde al eje de las ordenadas (eje Y). También se dice eje focal.
  • Vértice (V): es el punto de intersección entre la parábola y su eje.
  • Distancia focal: es la distancia entre el foco y el vértice, o entre la directriz y el vértice. Su valor siempre es igual a  \displaystyle \frac{p}{2}.
elementos de la parabola

Lado recto

El lado recto de una parábola es la cuerda comprendida dentro de la parábola que pasa por el foco y es paralela a la directriz.

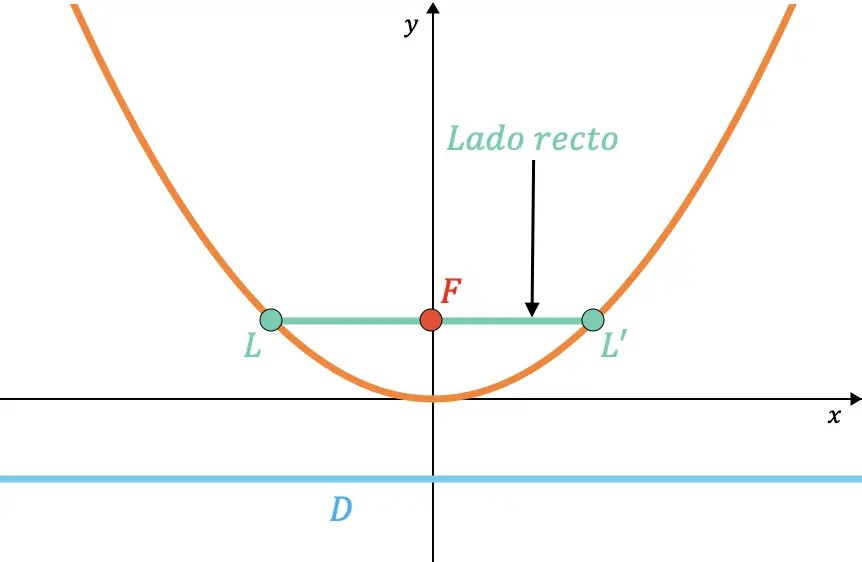
lado recto de una parabola

Asimismo, se puede demostrar que la longitud del lado recto siempre es el doble del valor del parámetro p.

\lvert LL'\rvert = 2p

Por otro lado, las dos rectas tangentes a la parábola que pasan por los extremos del lado recto forman un ángulo de 45º con el propio lado recto y, además, se cortan en el vértice de la parábola.

Ecuaciones de la parábola

La ecuación de una parábola es un tipo de función cuadrática porque siempre debe de tener com mínimo 1 término elevado al cuadrado. Además, la ecuación de una parábola depende de si esta está orientada horizontalmente o verticalmente.

Así pues, en geometría analítica existen varias maneras de expresar matemáticamente una parábola: la ecuación canónica o reducida, la ecuación ordinaria y la ecuación general de la parábola.

Ecuación reducida o canónica de la parábola

Lo que diferencia la ecuación reducida o canónica de las otras ecuaciones parabólicas, es que el vértice de la parábola es el origen de coordenadas, es decir, el punto (0,0).

La forma de la ecuación reducida de la parábola depende de si esta es horizontal o vertical. Fíjate en la siguiente representación gráfica donde se muestran las 4 posibles variantes:

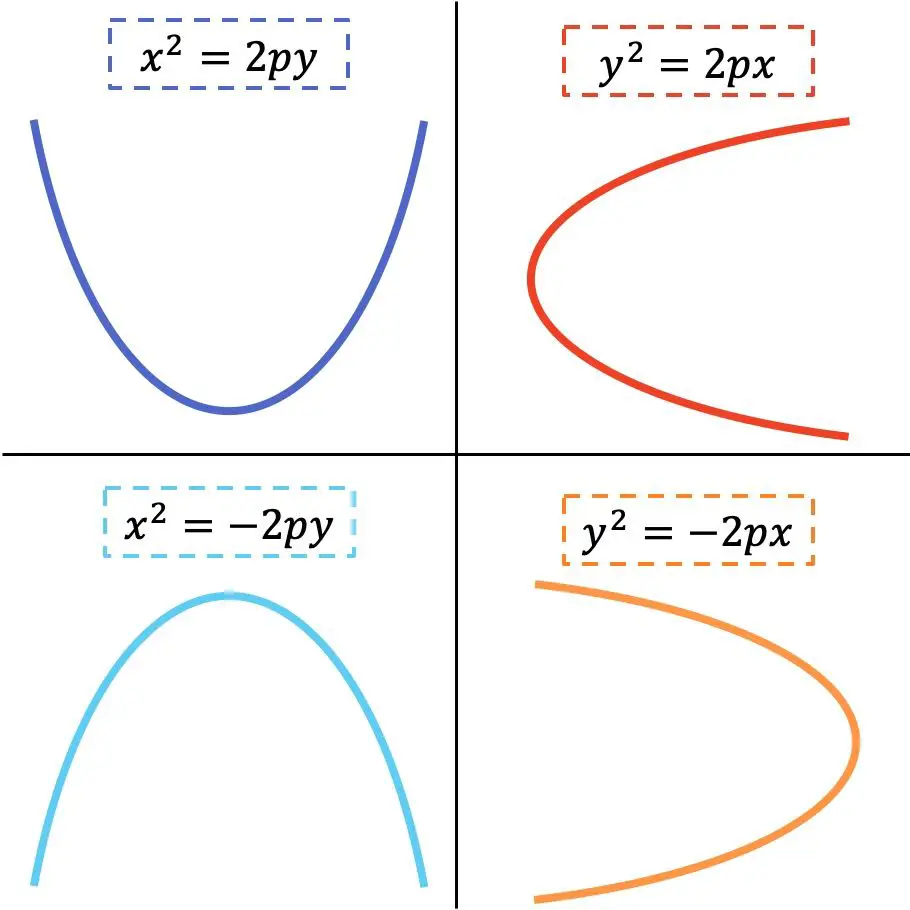
ecuacion de la parabola

Donde p es el parámetro característico de la parábola.

Com ves en la imagen anterior, cuando la variable x está elevada al cuadrado la parábola es vertical, en cambio, cuando la variable y está elevada al cuadrado la parábola es horizontal. Por otra parte, el sentido de las ramas de la parábola depende del signo de la ecuación.

Ecuación ordinaria de la parábola

Acabamos de ver cómo es la ecuación de la parábola cuando su vértice o centro corresponde al origen de coordenadas (la ecuación reducida o canónica), pero ¿cuál es la ecuación de la parábola si el vértice está fuera del origen?

Cuando el vértice de la parábola es un punto cualquiera utilizamos la ecuación ordinaria de la parábola, cuya expresión es:

\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}

Donde el centro o vértice de la parábola es el punto V(x_0,y_0).

La ecuación anterior corresponde a la parábola que está orientada de manera vertical, o dicho con otras palabras, el eje focal de la parábola es paralelo al eje Y.

Análogamente, para definir una parábola orientada de manera horizontal (su eje focal es paralelo al eje X), debemos usar la siguiente variante de la ecuación ordinaria de la parábola:

\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}

Donde, al igual que antes, el centro o vértice de la parábola es el punto V(x_0,y_0).

Ecuación general de la parábola

Hasta ahora todas las ecuaciones de las parábolas que hemos analizado sirven para expresar parábolas horizontales o verticales. Pero, evidentemente, una parábola también puede ser oblicua o inclinada.

Pues para expresar este tipo de parábolas se usa la ecuación general de la parábola, cuya fórmula es la siguiente:

\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}

La ecuación anterior se trata de una parábola si, y solo si, los coeficientes A y C no son simultáneamente nulos y, además, se cumple la siguiente condición:

B^2-4AC =0

Ejemplo de cómo hallar el vértice, el foco y la directriz de una parábola a partir de su ecuación

En muchos ejercicios y problemas de parábolas se pide calcular el vértice, el foco y la directriz de una determinada parábola. Por tanto, vamos a ver cómo se hace mediante un ejemplo:

  • Halla el vértice, el foco y la directriz de la siguiente parábola:

x^2 = 4y

Lo fundamental para resolver este tipo de problemas de parábolas es determinar el parámetro p de la parábola. En este caso, la ecuación de la parábola corresponde a la ecuación reducida o canónica (parábola vertical):

x^2 = 2py

Por lo tanto, el parámetro p es:

2p = 4

p = \cfrac{4}{2}

p = 2

Por otro lado, como la parábola sigue la ecuación reducida o canónica, significa que su vértice o centro está en el origen de coordenadas:

\bm{V(0,0)}

Una vez sabemos el vértice y el valor del parámetro de la parábola, podemos hallar su foco y directriz fácilmente.

El término cuadrático de la ecuación es la variable x de manera que el eje de la parábola será paralelo al eje OY y, de hecho, como su vértice es el punto (0,0), el eje de la parábola será el propio eje OY. Entonces, el foco de una parábola siempre está situado en el eje de la parábola y a una distancia de p/2 del vértice de la parábola, por lo que sus coordenadas son:

\displaystyle F\left(0, \frac{p}{2} \right)

\displaystyle F\left(0, \frac{2}{2} \right)

\displaystyle \bm{F\left(0,1 \right)}

Del mismo modo, la recta directriz será la recta horizontal que está a una distancia p/2 del vértice de la parábola, que es el origen de coordenadas. Por tanto, la ecuación de la recta directriz será:

y=-\cfrac{p}{2}

y=-\cfrac{2}{2}

\bm{y=-1}}

A continuación se ha representado gráficamente la parábola para que puedas comprobar los resultados:

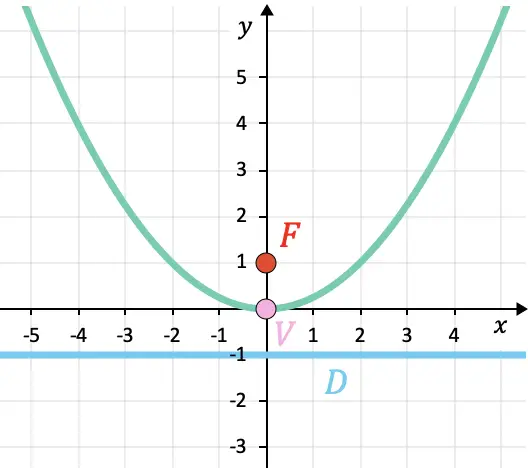
ejercicios resueltos de ecuacion de la parabola

Propiedades de las parábolas

Todas las parábolas poseen las siguientes propiedades:

  • Una parábola se trata de una curva abierta, o dicho de otra forma, consiste en dos ramas sin puntos comunes que se prolongan ilimitadamente.
  • Toda parábola tiene un único eje de simetría, donde está situado el vértice de dicha parábola.
  • Una parábola de orientación vertical es convexa cuando sus ramas van hacia arriba, por contra, la parábola es cóncava si sus ramas van hacia abajo.
  • La excentricidad de una parábola es equivalente a la unidad (1). La excentricidad es un coeficiente que en este caso se calcula dividiendo la distancia desde el foco hasta el centro de la parábola entre la distancia del vértice a la directriz (y ambas distancias siempre coinciden en su valor).
  • De la propiedad anterior, se deriva que todas las parábolas son semejantes o similares.
  • Una parábola no tiene ninguna asíntota.

Aplicaciones de la parábola

Ahora que ya conoces de sobras el significado de una parábola, puede que te estés preguntando… ¿para qué sirve una parábola?

Pues, aunque quizá no te lo parece, la forma geométrica de una parábola es muy común en la vida real. Por ejemplo, muchas veces al lanzar una pelota esta realiza un movimiento parabólico, especialmente en baloncesto. Pues la ecuación de la parábola es muy útil para estudiar analíticamente la trayectoria parabólica que sigue la pelota.

Otra aplicación de la parábola es para las antenas (de ahí el nombre antena parabólica). Ya que todo rayo que incide sobre un objeto de forma parabólica paralelamente al eje de simetría se refleja directamente hacia el foco, es decir, todos los rayos que van a la antena parabólica quedan concentrados en el foco y esto se puede aprovechar de varias maneras. Por eso mismo es tan importante el foco de una parábola.

Ejercicios resueltos de parábolas

Ejercicio 1

Calcula el vértice, el foco y la directriz de la parábola cuya ecuación es la siguiente:

y^2 = 8x

En primer lugar, la parábola será horizontal porque sigue la siguiente expresión de la ecuación reducida o canónica de la parábola:

y^2 = 2px

Así que su parámetro p es:

2p = 8

p = \cfrac{8}{2}

p = 4

Por otra parte, como la parábola sigue la ecuación reducida o canónica, significa que su vértice o centro está en el origen de coordenadas:

\bm{V(0,0)}

Una vez sabemos el vértice y el valor del parámetro de la parábola, podemos calcular su foco y directriz de manera fácil.

El término cuadrático de la ecuación es la variable y osea que el eje de la parábola será paralelo al eje OX y, de hecho, como su vértice es el punto (0,0), el eje de la parábola será el propio eje OX. Entonces, el foco de una parábola siempre está situado en el eje de la parábola y a una distancia de p/2 del vértice de la parábola, con lo que sus coordenadas son:

\displaystyle F\left(\frac{p}{2},0\right)

\displaystyle F\left(\frac{4}{2},0\right)

\displaystyle \bm{F\left(2,0 \right)}

Del mismo modo, la recta directriz está a una distancia p/2 del vértice de la parábola, que es el origen de coordenadas y es perpendicular a su eje focal. Por tanto, la ecuación de la recta directriz es:

x=-\cfrac{p}{2}

x=-\cfrac{4}{2}

\bm{x=-2}}

 

Ejercicio 2

Halla el vértice, el foco y la directriz de la parábola cuya ecuación es la siguiente:

(x-4)^2 = -16(y+1)

La parábola está definida según su ecuación ordinaria (eje paralelo al eje Y), cuya fórmula es:

(x-x_0 )^2 = 2p (y-y_0)

Así que su parámetro p es:

2p = -16

p =- \cfrac{16}{2}

p =- 8

Por otra parte, en este caso la ecuación ordinaria de la parábola implica que su centro no está en el origen de coordenadas, por contra, las coordenadas cartesianas del vértice de la parábola son los números de los paréntesis cambiados de signo:

\bm{V(4,-1)}

Una vez sabemos el vértice y el valor del parámetro de la parábola, podemos calcular su foco y directriz.

El término cuadrático de la ecuación es la variable x por lo que que el eje de la parábola será paralelo al eje OY. Así pues, el foco de una parábola siempre está situado en el eje de la parábola y a una distancia de p/2 del vértice de la parábola, de modo que las coordenadas del foco son las del vértice sumando p/2 verticalmente:

\displaystyle F\left(4,-1+\frac{p}{2}\right)

\displaystyle F\left(4,-1+\frac{-8}{2}\right)

\displaystyle F\left(4,-1-4\right)

\displaystyle \bm{F\left(4,-5 \right)}

Del mismo modo, la directriz será la recta horizontal situada a una distancia p/2 del vértice de la parábola. Por lo tanto, la ecuación de la recta directriz es:

y=-1-\cfrac{-p}{2}

y=-1-\cfrac{-8}{2}

y=-1+4

\bm{y=3}}

 

Ejercicio 3

Determina la ecuación parábola cuyo eje es paralelo al eje de las abscisas, tiene como vértice el punto V(5,2) y su foco es el punto P(8,2).

En este caso, el vértice de la parábola no es el origen de coordenadas, por lo que necesitamos la ecuación ordinaria para definir la parábola del enunciado. Además, el eje focal de la parábola es paralelo al eje X, lo que significa que la parábola estará orientada horizontalmente (las ramas irán hacia la derecha o hacia la izquierda) y, por tanto, el término cuadrático de la ecuación debe ser la variable y:

(y-y_0 )^2 = 2p (x-x_0)

Luego, podemos sustituir las coordenadas del vértice de la parábola en la ecuación:

(y-2)^2 = 2p (x-5)

Ahora debemos encontrar cuánto vale el parámetro p. La distancia del foco al vértice tiene que ser p/2, por lo tanto, podemos hallar el valor del parámetro p de la siguiente ecuación:

\left. \begin{array}{c} V(5,2) \\[2ex] P(8,2) \end{array} \right\} \longrightarrow \ 8-5 = \cfrac{p}{2}

8-5 = \cfrac{p}{2}

3 = \cfrac{p}{2}

3\cdot 2 = p

6 = p

Finalmente, la ecuación de la parábola es:

(y-2)^2 = 2p (x-5)

(y-2)^2 = 2\cdot 6 (x-5)

\bm{(y-2)^2 = 12 (x-5)}

 

16 comentarios en “Parábola (matemáticas): definición, ecuación, elementos, ejemplos,…”

    1. Geometría Analítica

      ¡Me alegro mucho Evelyn! ¡Espero que te vaya todo genial! 😉😘😍

  4. Astryd

    Muchas gracias, una información contundente y entendible, me sirvió de mucho para mi examén de mañana¡👏👍😉

    Responder
    1. Geometría Analítica

      ¡Muchísimas gracias Astryd! ¡Seguro que consigues muy buena nota en el examen! 😉

    1. Geometría Analítica

      Hola Elizabeth, las parábolas de los ejercicios no están graficadas. Para representarlas gráficamente debes despejar una variable, calcular varios puntos y representarlos en una gráfica y luego unirlos.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio