▷ TODO sobre la recta: qué es, tipos, ejemplos, su ecuación (fórmulas),...

Explicación de todo sobre la recta: qué es, los diferentes tipos que hay, cómo expresar una recta matemáticamente (ecuaciones), cuáles son las posiciones relativas de las rectas, cómo calcular el ángulo que forman dos rectas, la interpretación de la pendiente de una recta,….

Índice

¿Qué es una recta?

La definición matemática de la recta es la siguiente:

Una recta es un conjunto infinito de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Por otro lado, una recta corresponde a la mínima distancia posible entre dos puntos diferentes.

Además, una recta se trata de una línea que se extiende en una misma dirección, por lo tanto, tiene una sola dimensión.

Tipos de rectas

Acabamos de ver qué son las rectas pero debes saber que hay más de un tipo de rectas, cada uno con sus características. Así pues, las rectas se pueden clasificar de la siguientes manera:

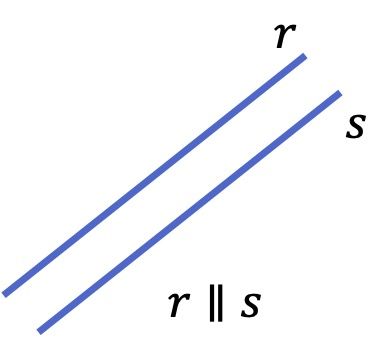
Rectas paralelas

Las rectas paralelas son aquellas líneas que nunca se cortan, es decir, aunque se prolonguen sus trayectorias hasta el infinito nunca llegan a tocarse. Por lo tanto, los puntos de dos rectas paralelas siempre están a una misma distancia entre sí y, además, dos rectas paralelas no tienen ningún punto en común.

Rectas secantes

En matemáticas, dos rectas son secantes cuando se cortan únicamente en un punto. Por lo tanto, las rectas que son secantes tienen un solo punto en común.

Un ejemplo de rectas secantes son rectas las perpendiculares, que son las rectas que se cortan en un punto formando cuatro ángulos rectos (de 90º) iguales.

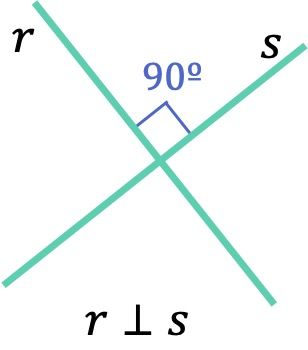
Como bien sabes, las rectas perpendiculares son muy importantes y, por tanto, tenemos una página con la explicación de todo lo que debes saber sobre este tipo de rectas: cuándo dos rectas son perpendiculares, cómo calcular una recta perpendicular a otra, ejemplos y ejercicios resueltos de rectas perpendiculares y mucho más. Así que te dejo la página de la perpendicularidad entre rectas por si quieres saber más.

Por otra parte, las rectas que son secantes pero no se cruzan formando un ángulo de 90º, sino otro ángulo, se llaman rectas oblicuas.

Rectas coincidentes

Dos rectas coincidentes son dos líneas que tienen todos sus puntos en común. Por lo tanto, dos rectas coincidentes son completamente idénticas.

Semirrecta

Se denomina semirrecta a cada una de las dos partes en que queda dividida una recta al cortarla por cualquiera de sus puntos.

Por ejemplo, la recta anterior puede ser dividida por el punto A, formando así las semirrectas $s$ y $t.$

Ecuación de la recta

En geometría analítica, para expresar analíticamente cualquier recta se utilizan las ecuaciones de la recta. Y para hallar la ecuación de una recta, ya sea en el plano (en R2) o en el espacio (en R3), solamente se necesita un punto que pertenezca a la recta y el vector director de dicha recta.

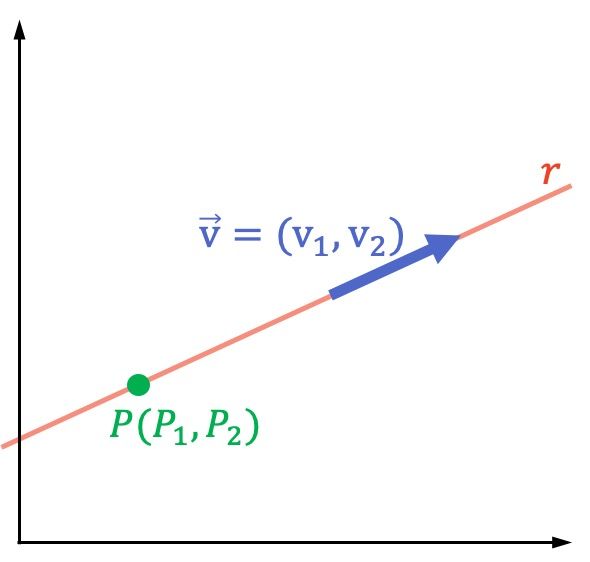
Como puedes ver en la representación gráfica de la recta anterior, las rectas se nombran por una letra minúscula, en este caso $r.$

Existen muchos tipos de ecuaciones de la recta. Todos los tipos de ecuaciones de la recta sirven para lo mismo: representar matemáticamente una recta. Pero cada ecuación de la recta tiene sus propiedades y, por lo tanto, dependiendo del problema es mejor usar una u otra. A continuación tienes las fórmulas de todas las ecuaciones de la recta.

Ecuación vectorial de la recta

Si $\vv{\text{v}}$ es el vector director de la recta y $P$ un punto que pertenece a la recta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La fórmula de la ecuación vectorial de la recta es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ es un escalar (un número real) cuyo valor depende de cada punto de la recta.

Ecuaciones paramétricas de la recta

La fórmula de la ecuación paramétrica de una recta es la siguiente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$ es un escalar (un número real) cuyo valor depende de cada punto de la recta.

Ecuación continua de la recta

La fórmula de la ecuación continua de la recta es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
$P_1$ y $P_2$ son las coordenadas de un punto conocido que forma parte de la recta $P(P}_1,P_2).$
$\text{v}_1$ y $\text{v}_2$ son las componentes del vector director de la recta $\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Ecuación implícita o general de la recta

Si $\vv{\text{v}}$ es el vector director de la recta y $P$ un punto que pertenece a la recta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La fórmula de la ecuación implícita, general o cartesiana de la recta es:

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
El coeficiente $A$ es la segunda componente del vector director de la recta: $A=\text{v}_2}$
El coeficiente $B$ es la primera componente del vector director cambiada de signo: $B=-\text{v}_1}$
El coeficiente $C$ se calcula sustituyendo el punto conocido $P$ en la ecuación de la recta.

A parte de con la fórmula, también se puede obtener la ecuación implícita de una recta multiplicando en cruz las fracciones de la ecuación continua.

Ecuación explícita de la recta

La fórmula de la ecuación explícita de la recta es:

Donde:

$m$ es la pendiente de la recta.
$n$ su ordenada en el origen, es decir, la altura a la que corta el eje Y.

En este caso particular, otra forma de calcular la ecuación explícita es a través de la ecuación implícita; para ello simplemente se debe despejar la variable $y$ de la ecuación implícita.

Ecuación punto-pendiente de la recta

La fórmula de la ecuación punto-pendiente de la recta es:

Donde:

$m$ es la pendiente de la recta.
$P_1, P_2$ son las coordenadas de un punto que pertenece a la recta $P(P_1,P_2).$

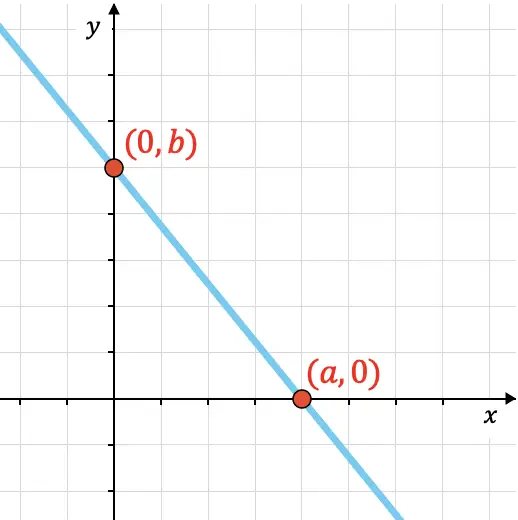
Ecuación canónica o segmentaria de la recta

Aunque esta variante de la ecuación de la recta es menos conocida, la ecuación canónica de la recta se puede obtener a partir de los puntos de corte de la recta con los ejes cartesianos.

Sean los dos puntos de intersección con los ejes de una recta determinada:

Corte con el eje X: $(a,0)$

Corte con el eje Y: $(0,b)$

La fórmula de la ecuación canónica de la recta es:

Acabamos de ver las fórmulas de todas las ecuaciones de la recta, pero si quieres puedes profundizar más y practicar con ejercicios de las ecuaciones de la recta. Además, en esta página podrás ver una explicación más detallada de las ecuaciones de la recta y ejemplos de cómo se calculan todos los tipos de ecuaciones de una recta.

Significado de la pendiente de una recta

Con toda la información de arriba ya sabemos completamente cómo es la ecuación de una recta y que una manera de describir una recta es a partir de su pendiente. Pero realmente… ¿qué significa la pendiente de una recta?

La pendiente de una recta indica las unidades verticales que sube la recta por cada unidad horizontal de la gráfica.

Por ejemplo, en la representación de la siguiente recta puedes ver que avanza 2 unidades verticales por cada unidad horizontal, porque su pendiente es igual a 2.

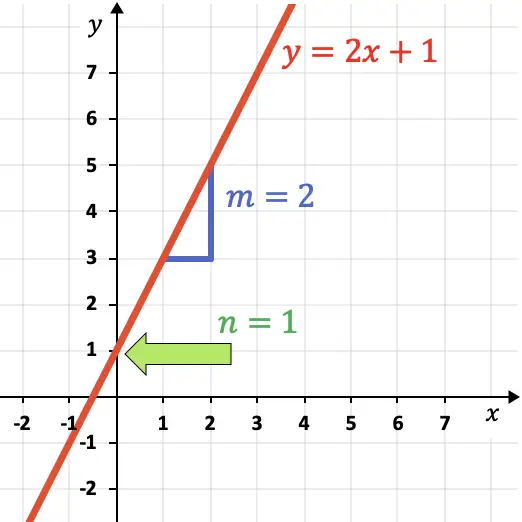
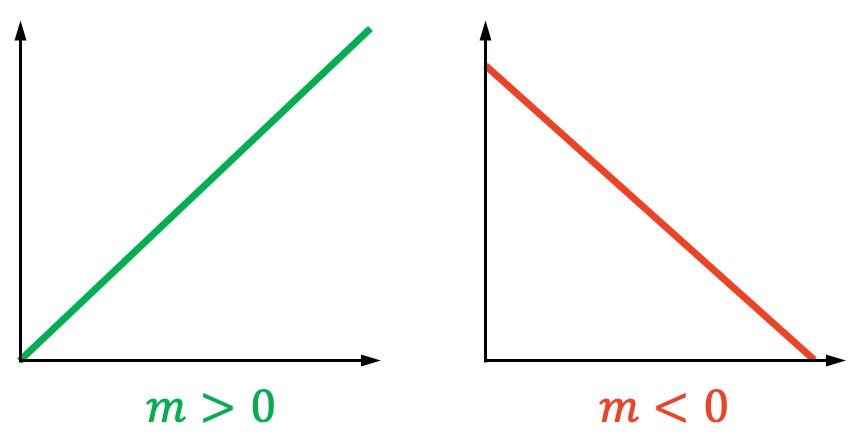
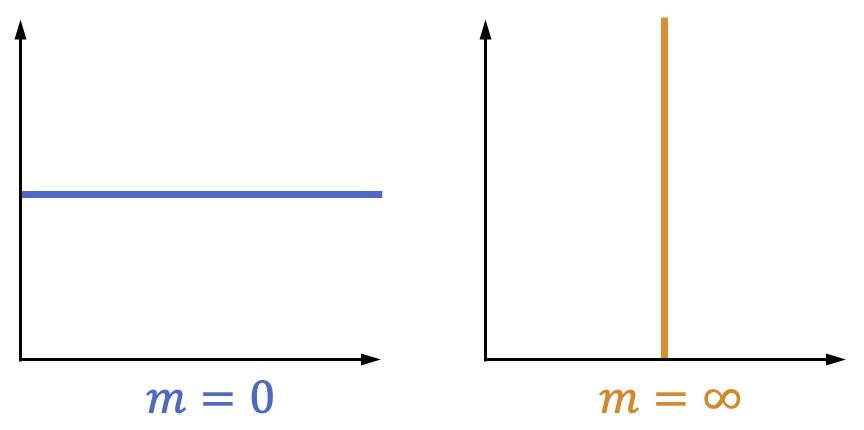
Además, la pendiente de una recta también indica su inclinación:

Si una recta es creciente (va hacia arriba), su pendiente es positiva.
Si una recta es decreciente (va hacia abajo), su pendiente es negativa.
Si una recta es completamente horizontal, su pendiente es igual a 0.
Si una recta es totalmente vertical, su pendiente es equivalente a infinito.

pendiente de una recta positiva o negativa

Posición relativa de dos rectas en el plano

Cuando trabajamos con dos dimensiones (en R2), existen 3 posibles tipos de posiciones relativas entre dos rectas:

Rectas secantes

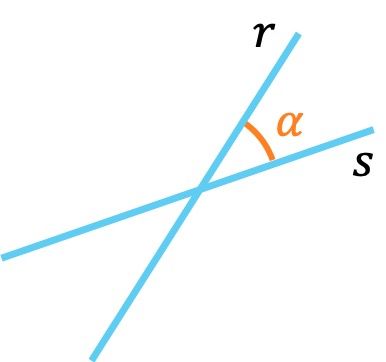
Dos rectas secantes tienen un solo punto en común.

Rectas paralelas

Dos rectas son paralelas si no tienen ningún punto en común. Es decir, si nunca se cruzan.

Rectas coincidentes

Dos rectas son coincidentes si todos sus puntos son comunes.

Por otro lado, el ángulo entre dos rectas en el plano también depende de su posición relativa:

Las rectas secantes se cortan formando un ángulo entre 0º (no incluido) y 90º (incluido). Además, si justo hacen un ángulo recto de 90º, significa que las dos rectas son perpendiculares.
Las rectas paralelas forman un ángulo de 0º, ya que tienen la misma dirección.
Y, por la misma razón, las rectas coincidentes también forman un ángulo de 0º entre sí.

Ángulo entre dos rectas

Existen varios método para calcular el ángulo que forman dos rectas y algunos son bastante complicados, así que explicaremos la manera más fácil de determinar el ángulo entre 2 rectas.

La fórmula para calcular el ángulo entre dos rectas mediante sus vectores directores es la siguiente:

Dados los vectores directores de dos rectas distintas:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

El ángulo que forman estas dos rectas se puede calcular con la siguiente fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Donde $\lvert \vv{\text{u}} \rvert$ y $\lvert \vv{\text{v}} \rvert$ son los módulos de los vectores $\vv{\text{u}}$ y $\vv{\text{v}}$ respectivamente.

Recordemos que la fórmula del módulo de un vector es:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Evidentemente, una vez hemos calculado el coseno del ángulo que forman las dos rectas a través de la fórmula, debemos invertir el coseno para averiguar el valor del ángulo.

La recta: definición, características, tipos, ecuación…

¿Qué es una recta?

Tipos de rectas

Rectas paralelas

Rectas secantes

Rectas coincidentes

Semirrecta

Ecuación de la recta

Ecuación vectorial de la recta

Ecuaciones paramétricas de la recta

Ecuación continua de la recta

Ecuación implícita o general de la recta

Ecuación explícita de la recta

Ecuación punto-pendiente de la recta

Ecuación canónica o segmentaria de la recta

Significado de la pendiente de una recta

Posición relativa de dos rectas en el plano

Ángulo entre dos rectas

2 comentarios en “La recta: definición, características, tipos, ecuación…”

Deja un comentario Cancelar respuesta