▷ ¿Cómo se calcula el ángulo entre dos vectores? (fórmula) ✅

En esta página encontrarás cómo se calcula el ángulo entre dos vectores. Además, también verás ejemplos y podrás practicar con ejercicios y problemas resueltos paso a paso.

Índice

Fórmula del ángulo entre dos vectores

angulo entre dos vectores a partir del producto escalar

Si recordamos la definición del producto escalar, este se puede calcular mediante la siguiente ecuación:

$\displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert \cdot \cos(\alpha )$

A partir de esta igualdad, podemos conseguir la fórmula que nos servirá para encontrar directamente el ángulo que forman dos vectores:

El coseno del ángulo que forman dos vectores es igual al producto escalar entre los dos vectores dividido por el producto de los módulos de los dos vectores.

Es decir, la fórmula para determinar el ángulo que forman dos vectores es la siguiente:

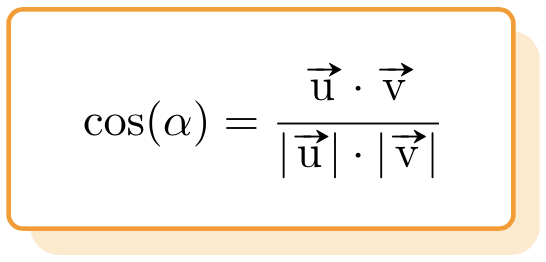
Por lo tanto, para poder encontrar el ángulo que forman dos vectores es imprescindible que sepas cómo calcular el módulo de un vector. En este enlace encontrarás la fórmula, ejemplos y ejercicios resueltos del módulo de un vector, así que si aún no dominas esta operación vectorial te recomendamos que le eches un vistazo.

Esta fórmula sirve tanto para el plano (en R2) como para el espacio (en R3). Es decir, la podemos utilizar indistintamente para vectores con dos o tres componentes.

Sin embargo, en ocasiones no es necesario aplicar esta fórmula porque se puede deducir el ángulo que hay entre los vectores:

El ángulo entre dos vectores perpendiculares (que tienen la misma dirección) es de 0º.
El ángulo entre dos vectores ortogonales (o perpendiculares) es de 90º.

Ejemplo de cómo hallar el ángulo entre dos vectores

A modo de ejemplo, vamos a calcular el ángulo que forman los siguientes dos vectores:

$\vv{\text{u}} = (4,-1) \qquad \vv{\text{v}} = (2,5)$

Primero tenemos que calcular el módulo de cada vector:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{2^2+5^2}= \sqrt{29}$

Ahora usamos la fórmula para calcular el coseno del ángulo que hay entre los dos vectores:

$\displaystyle \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}=\cfrac{ 4\cdot 2 + (-1)\cdot 5}{\sqrt{17}\cdot \sqrt{29}} = \cfrac{3}{\sqrt{493}} = 0,14$

Y, por último, hallamos el ángulo correspondiente haciendo la inversa del coseno mediante la calculadora:

$\displaystyle \cos^{-1}(0,14) = \bm{81,95º}$

Por lo tanto, los dos vectores forman un ángulo de 81,95º.

Ejercicios resueltos de ángulos entre vectores

Ejercicio 1

Calcula el ángulo entre los siguientes dos vectores:

$\displaystyle \vv{\text{u}}=(5,3) \qquad \vv{\text{v}} =(1,2)$

Ver solución

En primer lugar, tenemos que calcular el módulo de ambos vectores:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{5^2+3^2}= \sqrt{34}$

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ 1^2+2^2}= \sqrt{5}$

Utilizamos la fórmula para calcular el coseno del ángulo que forman los vectores:

$\displaystyle \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}=\cfrac{ 5\cdot 1 + 3\cdot 2}{\sqrt{34}\cdot \sqrt{5}} = \cfrac{11}{\sqrt{170}} = 0,84$

Finalmente, encontramos el ángulo correspondiente haciendo la inversa del coseno con la calculadora:

$\displaystyle \cos^{-1}(0,84) = \bm{32,47º}$

Ejercicio 2

Determina el ángulo que existe entre los siguientes dos vectores:

$\displaystyle \vv{\text{u}}=(-2,-7) \qquad \vv{\text{v}} =(-1,5)$

Ver solución

Primero de todo debemos encontrar los módulos de los vectores:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ (-2)^2+(-7)^2}= \sqrt{53}$

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ (-1)^2+5^2}= \sqrt{26}$

Usamos la fórmula para sacar el coseno del ángulo que tienen los vectores:

$\displaystyle \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}=\cfrac{ (-2)\cdot (-1) + (-7)\cdot 5}{\sqrt{53}\cdot \sqrt{26}} = \cfrac{-33}{\sqrt{1378}} = -0,89$

Y, por acabar, hallamos el ángulo correspondiente haciendo la inversa del coseno con la calculadora:

$\displaystyle \cos^{-1}(-0,89) = \bm{152,74º}$

Ejercicio 3

Calcula el valor de $k$ para que los siguientes vectores sean perpendiculares:

$\displaystyle \vv{\text{u}}=(6,3) \qquad \vv{\text{v}} =(-4,k)$

Ver solución

Dos vectores que son perpendiculares forman un ángulo de 90º. Por tanto:

$\displaystyle \cos(90º) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

$\displaystyle 0=\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

El denominador de la fracción está dividiendo todo el lado derecho de la ecuación, así que podemos pasarlo multiplicando al otro lado:

$\displaystyle 0 \cdot \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert =\vv{\text{u}} \cdot \vv{\text{v}}$

$\displaystyle 0 =\vv{\text{u}} \cdot \vv{\text{v}}$

Ahora resolvemos el producto escalar:

$\displaystyle 0 =(6,3) \cdot (-4,k)$

$\displaystyle 0 =6 \cdot (-4) + 3\cdot k$

$\displaystyle 0 =-24 +3k$

Y, finalmente, despejamos la incógnita:

$\displaystyle -3k =-24$

$\displaystyle k =\cfrac{-24}{-3}$

$\displaystyle \bm{k =8}$

Ejercicio 4

Encuentra el valor que deben tener las constantes $a$ y $b$ para que los siguientes vectores sean perpendiculares y, además, se cumpla $\lvert \vv{\text{u}} \rvert =10.$

$\displaystyle \vv{\text{u}}=(-6,a) \qquad \vv{\text{v}} =(b,3)$

Ver solución

Primero utilizaremos la condición del módulo para hallar el valor de $a:$

$\lvert \vv{\text{u}} \rvert =10$

$\sqrt{(-6)^2+a^2}=10$

$\sqrt{36+a^2}=10$

Elevamos los dos miembros de la ecuación para quitar la raíz cuadrada:

$\left(\sqrt{36+a^2}\right)^2=10^2$

$36+a^2=100$

Y despejamos la incógnita:

$a^2=100 -36$

$a^2=64$

$a=\sqrt{64}$

$\bm{a=8}$

Una vez conocemos el valor de $a$ , vamos a encontrar el valor de $b$ aplicando la fórmula del ángulo de dos vectores, ya que el enunciado nos dice que deben ser perpendiculares, o lo que es equivalente, deben formar 90º.

$\displaystyle \cos(90º) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

$\displaystyle 0=\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

El denominador de la fracción está dividiendo todo el lado derecho de la ecuación, así que podemos pasarlo multiplicando al otro lado:

$\displaystyle 0 \cdot \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert =\vv{\text{u}} \cdot \vv{\text{v}}$

$\displaystyle 0 =\vv{\text{u}} \cdot \vv{\text{v}}$

Ahora intentamos resolver el producto escalar:

$\displaystyle 0 =(-6,8) \cdot (b,3)$

$\displaystyle 0 =-6 \cdot b +8\cdot 3$

$\displaystyle 0 =-6b +24$

Y, para acabar, despejamos la incógnita:

$\displaystyle 6b =24$

$\displaystyle b =\cfrac{24}{6}$

$\displaystyle \bm{b =4}$

Ejercicio 5

Calcula los ángulos $\alpha , \beta$ y $\gamma$ que forman los lados del siguiente triángulo:

ejercicios y problemas resueltos paso a paso del producto escalar de dos vectores

Ver solución

Los vértices que componen el triángulo son los siguientes puntos:

$A(2,1) \qquad B(4,4) \qquad C(6,2)$

Para calcular los ángulos internos del triángulo, podemos calcular los vectores de cada uno de sus lados y luego hallar el ángulo que forman a través de la fórmula del producto escalar.

Por ejemplo, para encontrar el ángulo $\alpha$ calculamos los vectores de sus lados:

$\vv{AB} = B - A = (4,4)-(2,1)= (2,3)$

$\vv{AC} = C - A = (6,2)-(2,1)= (4,1)$

Y hallamos el ángulo que forman los dos vectores mediante la fórmula del producto escalar:

$\lvert \vv{AB} \rvert = \sqrt{2^2+3^2} = \sqrt{13}$

$\lvert \vv{AC} \rvert = \sqrt{4^2+1^2} = \sqrt{17}$

$\displaystyle \cos(\alpha) =\cfrac{\vv{AB} \cdot \vv{AC}}{\lvert \vv{AB} \rvert \cdot \lvert \vv{AC} \rvert}=\cfrac{ 2\cdot 4 + 3\cdot 1}{\sqrt{13}\cdot \sqrt{17}} = \cfrac{11}{\sqrt{221}} =0,74$

$\bm{\alpha = 42,27º}$

Ahora repetimos el mismo procedimiento para determinar el ángulo $\beta:$

$\vv{BC} = C - B = (6,2)-(4,4)= (2,-2)$

$\lvert \vv{BC} \rvert = \sqrt{2^2+(-2)^2} = \sqrt{8}$

$\displaystyle \cos(\beta) =\cfrac{\vv{AB} \cdot \vv{BC}}{\lvert \vv{AB} \rvert \cdot \lvert \vv{BC} \rvert}=\cfrac{ 2\cdot 2 + 3\cdot (-2)}{\sqrt{13}\cdot \sqrt{8}} = \cfrac{-2}{\sqrt{104}} =-0,20$

$\bm{\beta = 101,31º}$

Finalmente, para encontrar el último ángulo podemos volver a hacer el mismo procedimiento. Sin embargo, todos los ángulos de un triángulo deben sumar 180º grados, por tanto:

$\gamma = 180 -42,27-101,31 = \bm{36,42º}$

Cómo calcular el ángulo entre dos vectores

Fórmula del ángulo entre dos vectores

Ejemplo de cómo hallar el ángulo entre dos vectores

Ejercicios resueltos de ángulos entre vectores

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Deja un comentario Cancelar respuesta