Resta de vectores

En esta página verás cómo restar dos vectores, tanto gráficamente como numéricamente. Para restarlos de manera gráfica existen tres métodos: el del paralelogramo, el del triángulo y el del polígono. Aquí podrás diferenciar las ventajas y los inconvenientes de cada método. Además, encontrarás ejemplos, ejercicios y problemas resueltos paso a paso.

¿Cómo se restan dos vectores gráficamente?

Hay varias maneras de restar vectores geométricamente. Obviamente, con todas ellas se obtiene el mismo resultado, pero explicaremos todos los métodos para que tú puedas escoger el que prefieras. 👌

Para restar solamente 2 vectores existen dos procedimientos gráficos: el método del paralelogramo y el método del triangulo. Sin embargo, si queremos resolver la resta de 3 o más vectores tenemos que usar el método del polígono.

Así pues, y sin enrollarme más, tienes las explicaciones de todos estos métodos a continuación.

Método o regla del paralelogramo

La regla del paralelogramo o método del paralelogramo es un procedimiento que permite hallar la resta de dos vectores mediante su representación gráfica de manera muy simple. Los pasos que se deben seguir para aplicar este proceso son:

1. Primeramente, representamos los dos vectores en la gráfica y los posicionamos en el mismo punto de aplicación, es decir, situamos los orígenes de los dos vectores en el mismo punto.
2. En segundo lugar, dibujamos el vector opuesto del vector que resta en la operación, o dicho con otras palabras, invertimos el vector que está restando.
3. Luego dibujamos una recta paralela al vector cambiado de signo en el extremo del vector que suma. Y repetimos el proceso con el otro vector. De forma que obtendremos el dibujo de un paralelogramo (por eso el nombre de la regla).
4. Por último, el resultado de la resta será el vector que va desde el origen en común de los dos vectores hasta el punto donde se cruzan las dos rectas paralelas.

Fíjate en el siguiente ejemplo genérico en el que se restan dos vectores mediante el método del paralelogramo:

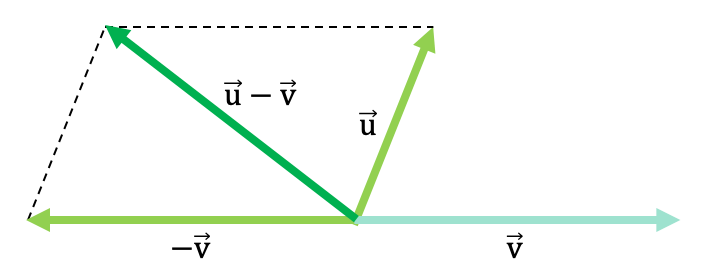
Método o regla del triángulo

El método del triángulo es otro procedimiento con el que se pueden restar dos vectores a partir de su gráfica. En este caso, los pasos que se tienen que hacer son:

1. Colocar los dos vectores en el mismo punto de aplicación, es decir, de manera que ambos vectores tengan como origen el mismo punto.
2. El resultado de la resta vectorial es el segmento que va desde el final del vector que resta hasta el extremo del otro vector. Si te fijas, se completa un triángulo con los dos vectores restados y el vector resta.

A continuación tienes un ejemplo de una resta de vectores con el método del triángulo:

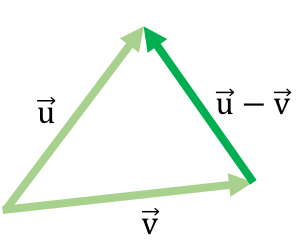
Esta forma de restar vectores es similar al método de cabeza y cola que se usa para sumar vectores.

Método del polígono

Una vez hemos visto cómo resolver la resta de dos vectores gráficamente, vamos a ver cómo se hace cuando tenemos más de dos vectores.

Cuando queremos restar tres o más vectores, existe una técnica para ir más rápido en el cálculo y restar todos los vectores a la vez. Esta técnica se llama método del polígono y consiste en aplicar sucesivamente el método de la cabeza-cola de la suma de vectores.

Ahora seguro que estás pensando: ¿de la suma de vectores? Esto está mal fijo… ¡Pues no! jeje

Resulta que restar dos vectores es equivalente a sumar un vector más el vector opuesto (o negado) del vector que resta. Esto es debido a las propiedades de la suma y la resta de vectores:

Por lo tanto, los pasos que debemos seguir para restar 3 o más vectores con el método del polígono son:

1. En primer lugar, tenemos que hallar el vector inverso de cada vector que resta. Es tan fácil como invertir de dirección y de sentido todos los vectores que están restando.
2. Luego, colocamos cada vector opuesto a continuación del vector que no está restando, uno detrás del otro. De manera que el origen de un vector coincida con el extremo de otro vector.
3. Finalmente, el resultado de la resta vectorial es el vector que se obtiene al unir el inicio del primer vector con el final del último vector.

Fíjate en el siguiente ejemplo donde se hace una resta con 4 vectores:

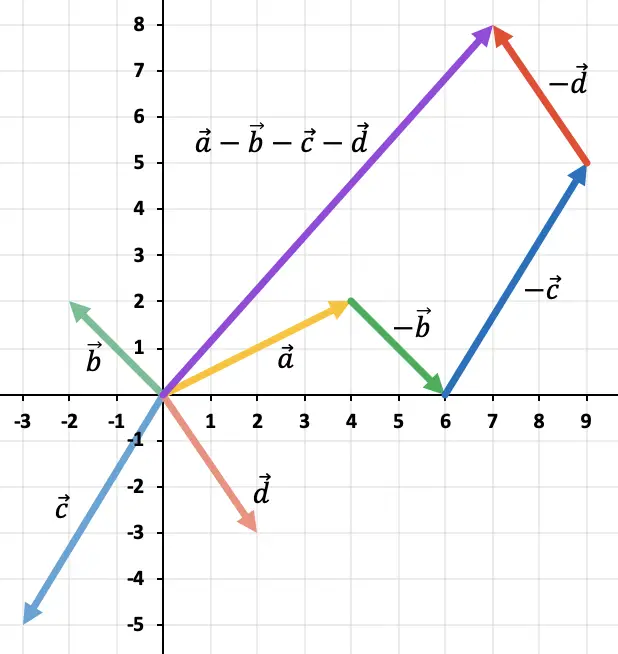
Fíjate que para hallar el vector opuesto de un vector se deben cambiar de signo las dos componentes de dicho vector.

¿Cómo calcular la resta de dos vectores numéricamente?

Una vez ya sabemos restar vectores a partir del gráfico, vamos a ver cómo calcular una resta vectorial numéricamente o algebraicamente.

Por ejemplo, la resta entre los vectores y es:

Ejercicios resueltos de resta de vectores

Ejercicio 1

Calcula gráficamente la resta de los vectores menos

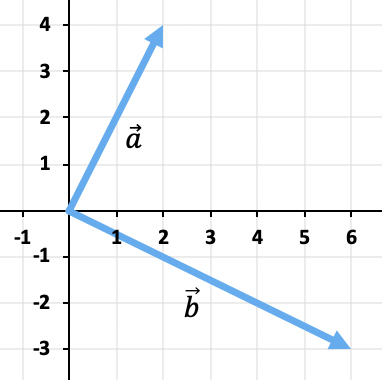
Para restar los dos vectores utilizaremos el método del triángulo. Los puntos ya están colocados en el mismo punto de aplicación (el origen de coordenadas), por lo que el resultado de la resta será el vector que va desde el extremo de hasta el extremo de

 

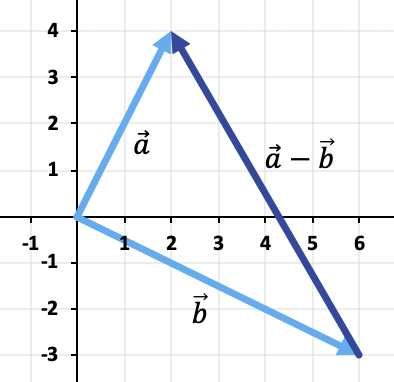
Ejercicio 2

Halla gráficamente la resta de los vectores menos

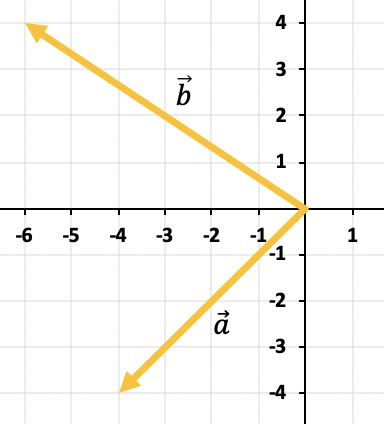
Para restar los dos vectores utilizaremos la regla del triángulo. Los puntos ya están colocados en el mismo punto de aplicación (al principio del eje X y del eje Y), con lo que el resultado de la resta será el vector que va desde el extremo de hasta el extremo de

 

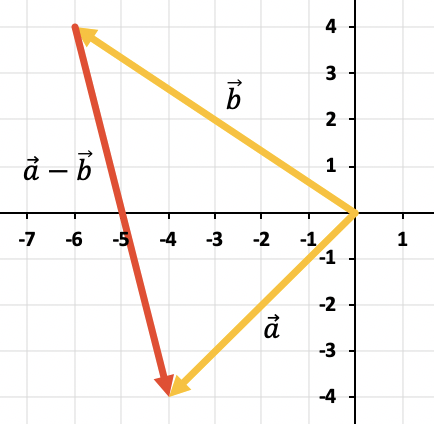
Ejercicio 3

Resuelve gráficamente la siguiente operación vectorial:

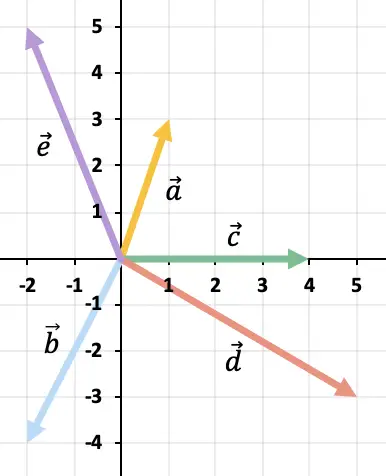
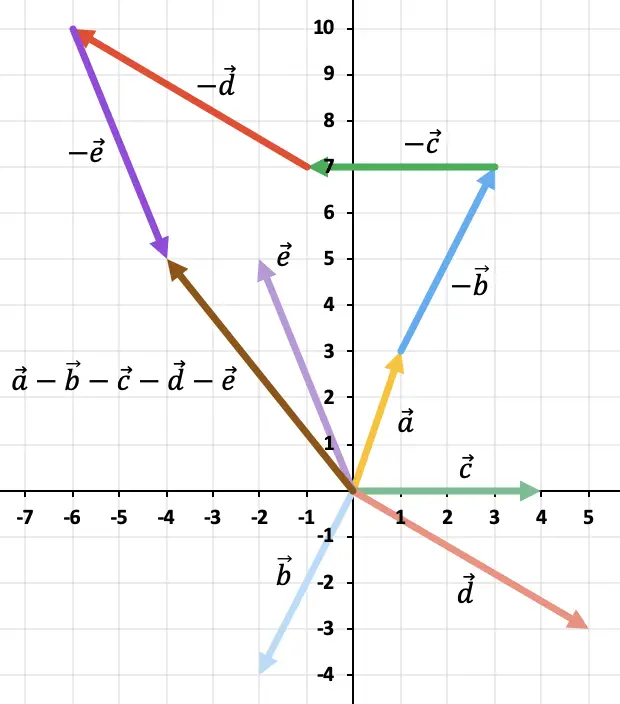
Como son más de 2 vectores, utilizaremos la regla del polígono para resolver la resta vectorial. Para ello, tenemos que representar los vectores opuestos de los vectores restantes uno detrás del otro. Y el resultado será el vector que va desde el origen del vector hasta donde termina el último vector opuesto.

 

Ejercicio 4

Determina el resultado de la resta de los siguientes vectores numéricamente:

Para restar dos vectores numéricamente debemos restar sus respectivas coordenadas:

 

Ejercicio 5

Resuelve la siguiente operación de vectores analíticamente:

Para restar vectores numéricamente (o analíticamente) debemos restar sus respectivas componentes: