Vectores (matemáticas): qué son, tipos, operaciones, ejemplos...

En esta página encontrarás todo sobre los vectores: qué son, sus características, cómo se calculan, cómo hacer operaciones con vectores, los diferentes tipos que hay,…

Índice

¿Qué es un vector?

La definición matemática de un vector es la siguiente:

En matemáticas, un vector es un segmento orientado que va desde un punto (llamado origen) hasta otro punto (llamado extremo).

Por ejemplo, en la representación gráfica siguiente puedes ver que el vector $\vv{AB}$ tiene como origen el punto A y como extremo el punto B.

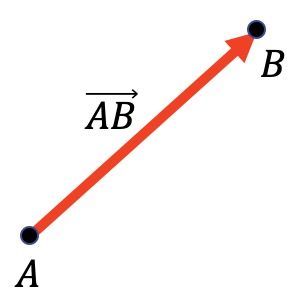
Los vectores se utilizan principalmente en matemáticas, especialmente en geometría, y en física, para representar gráficamente las fuerzas vectoriales.

Características de un vector

Una vez hemos visto cuál es el significado matemático de los vectores, veamos ahora qué propiedades tienen.

Todo vector tiene las siguientes características geométricas:

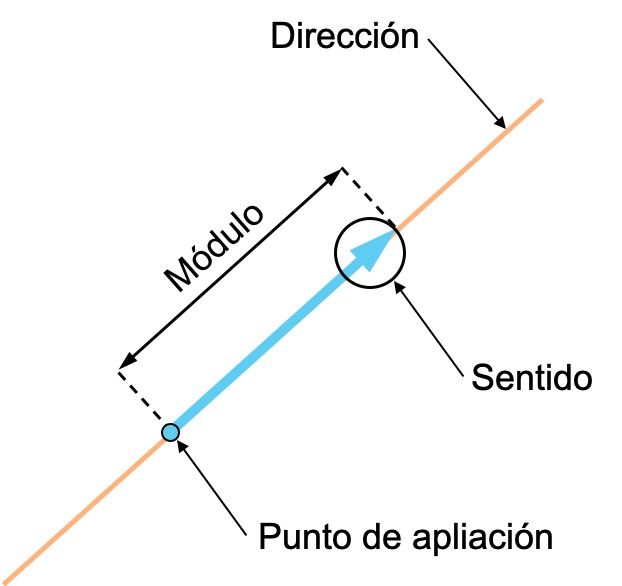
Dirección: la dirección de un vector corresponde a la dirección de la recta que contiene el vector o cualquier recta paralela a ella. Dicho con otras palabras, la dirección de un vector es la línea recta sobre la que está situado.
Sentido: el sentido de un vector es la orientación de dicho vector, lo indica su flecha.
Módulo (o magnitud): el módulo de un vector es su longitud, y corresponde al valor numérico del vector. Por lo tanto, cuanto mayor sea el vector significa que más grande es la magnitud vectorial que representa.
Punto de aplicación: el punto de aplicación de un vector es el origen de dicho vector.

caracteristicas geometricas de los vectores

Los conceptos de dirección y sentido de un vector dan lugar a confusiones muchas veces, por eso es importante distinguir la diferencia entre ellos. Fíjate en el siguiente ejemplo con dos vectores, ambos tienen la misma dirección pero sus sentidos son distintos:

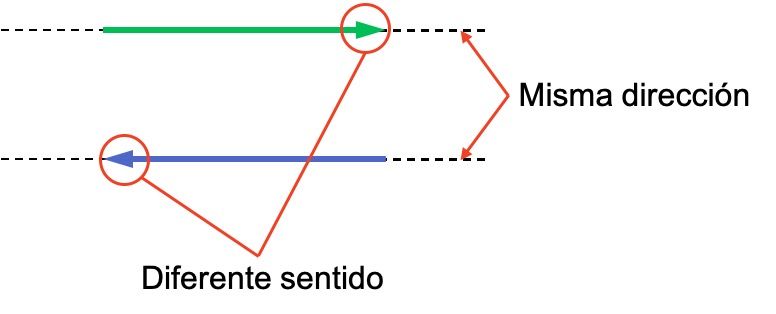
significado del sentido y direccion de un vector

Los dos vectores tienen la misma dirección porque son paralelos. En cambio, sus sentidos son opuestos ya que están orientados al revés.

Componentes de un vector

Acabamos de ver que los vectores se representan gráficamente mediante flechas, pero los vectores también se pueden representar numéricamente mediante las componentes (o coordenadas) de un vector.

Por ejemplo, si tenemos el siguiente vector representado en un gráfico:

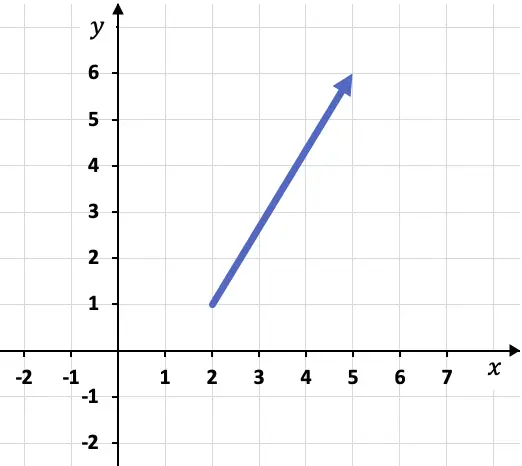
Para calcular las componentes del vector, primero tenemos que identificar las coordenadas de su origen y su extremo, es decir, los puntos donde empieza y donde termina. En este caso, el origen y el extremo del vector son:

Origen del vector: A(2,1)

Extremo del vector: B(5,6)

Entonces, para hallar las coordenadas o componentes del vector, simplemente debemos restar el extremo menos el origen:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

De modo que las componentes del vector representado en la gráfica son:

$\vv{\bm{AB}}\bm{=(3,5)}$

Operaciones con vectores

Suma de vectores

Para sumar dos vectores numéricamente se deben sumar sus respectivas componentes. O dicho de otra forma, se suman las coordenadas X de los dos vectores entre sí y lo mismo con las coordenadas Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Para que puedas ver cómo se hace, vamos a sumar los siguientes dos vectores:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

También se pueden sumar dos vectores a partir de sus representaciones gráficas. Para ello, normalmente se usa la regla o ley del paralelogramo, pero hay bastantes métodos. Puedes ver ejemplos y ejercicios resueltos de cómo sumar dos vectores gráficamente aquí.

Resta de vectores

Para restar dos vectores analíticamente se deben restar sus respectivas componentes. Es decir, se restan las coordenadas X de los dos vectores entre sí y lo mismo con las coordenadas Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

A modo de ejemplo, vamos a restar los siguientes dos vectores:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Igual que con la suma, también se pueden restar 2 vectores mediante sus representaciones. Para ello, se suele utilizar la regla o ley del triángulo, pero existen varios métodos. Puedes verlos todos junto con ejemplos y ejercicios resueltos en cómo restar dos vectores gráficamente.

Módulo de un vector

Como hemos visto al principio de esta página, el módulo de un vector corresponde a la longitud de dicho vector. Pues bien, la longitud (o magnitud) de un vector se puede determinar a partir de sus componentes.

Sea un vector cualquiera:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Para hallar el módulo de un vector en el plano se debe aplicar la siguiente fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Por ejemplo, vamos a calcular el módulo del siguiente vector utilizando la fórmula:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Aunque parece muy simple, determinar el módulo de un vector puede resultar complicado. Si quieres ver más ejemplos y practicar con ejercicios resueltos del módulo de un vector, te recomendamos que visites esta página enlazada.

Multiplicación de un vector por un escalar

Para calcular el producto de un vector por un número (o un escalar) numéricamente se debe multiplicar cada componente del vector por dicho número.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

En el siguiente ejemplo genérico puedes ver como la dirección del vector se mantiene independientemente del signo del escalar. En cambio, el sentido del vector sí que depende del signo del número que multiplica.

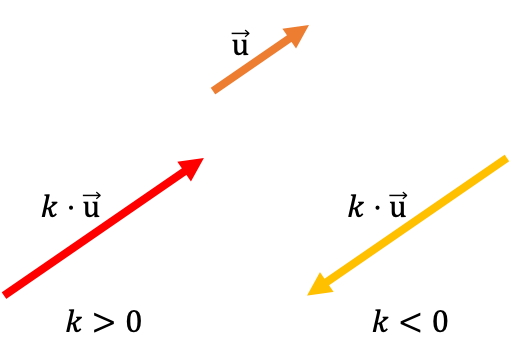
multiplicacion o producto de un numero o escalar por un vector

A continuación puedes ver un ejemplo numérico de cómo hallar el producto de un vector por un número:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Producto escalar

En geometría analítica, el producto escalar es una operación vectorial que multiplica dos vectores y los transforma en un un número real.

Así pues, la fórmula del producto escalar de dos vectores es la siguiente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

A continuación dispones de un ejemplo donde se calcula el resultado del producto escalar entre dos vectores:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

En este enlace puedes ver más ejemplos del producto escalar. Además, allí encontrarás otra forma de hallar el producto escalar entre dos vectores, las propiedades de este tipo de operación con vectores y ejercicios resueltos paso a paso.

Producto vectorial

Aunque su nombre es muy parecido, el producto escalar y el producto vectorial son completamente diferentes.

El producto vectorial, también llamado producto cruz, es una operación entre dos vectores en el espacio (en R3), es decir, intervienen vectores con tres coordenadas.

De manera que si tenemos dos vectores tridimensionales cualesquiera:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

El producto vectorial de los dos vectores es igual al resultado del siguiente determinante 3×3:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

Donde los vectores $\vv{i}, \vv{j},\vv{k}$ son los vectores unitarios en los sentidos de los ejes X, Y, Z respectivamente.

Además, la dirección del vector resultante es perpendicular a los dos vectores que se multiplican.

Como puedes suponer, resolver este tipo de operación es más difícil que las anteriores y, por eso mismo, tenemos toda una página con una explicación al detalle de cómo se calcula el producto vectorial entre dos vectores. Por lo que si estás interesad@ te recomendamos que la visites y practiques con los ejercicios resueltos del producto vectorial.

Producto mixto

El producto mixto de tres vectores, también conocido como triple producto escalar, es una multiplicación sucesiva entre tres vectores en la que intervienen dos tipos de operaciones diferentes: el producto escalar y el producto vectorial. De forma que la combinación de ambas operaciones vectoriales da como resultado un escalar (un número real).

Concretamente, el producto mixto consiste en calcular el producto vectorial de dos vectores y, posteriormente, en multiplicar vectorialmente el resultado obtenido por un tercer vector. Fíjate en la fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Al igual que con el producto vectorial, solucionar el producto mixto entre vectores no es nada fácil. Por esta razón, te recomendamos que le eches un vistazo a esta explicación del producto mixto de tres vectores, donde encontrarás ejemplos, ejercicios resueltos y el significado geométrico de esta operación vectorial.

Tipos de vectores

Existen muchos tipos diferentes de vectores, pero las definiciones más importantes que debes conocer son las siguientes:

Vector unitario: vector cuyo módulo es igual a 1.
Vector fijo: un vector es fijo cuando el origen del vector está aplicado a un punto fijo.
Vector libre: un vector es libre cuando su punto de aplicación no está definido, sino que es un punto libre.
Vectores colineales: dos o más vectores son colineales si comparten la misma recta de acción (recta donde se sitúa el vector).
Vectores equipolentes: dos vectores son equipolentes si tienen el mismo módulo, el mismo sentido y la misma dirección (anque pueden tener distinto punto de aplicación).
Vectores ligados: los vectores ligados son vectores equipolentes que, además, actúan en la misma recta.
Vectores opuestos: dos vectores son opuestos si tienen módulo y dirección equivalentes pero diferente sentido.
Vector de posición: el vector de posición es aquel vector que tiene como origen el punto (0,0) (origen de coordenadas).
Vectores concurrentes: dos o más vectores son concurrentes cuando sus líneas de acción pasan por el mismo punto, es decir, se cortan.
Vectores paralelos: dos o más vectores son paralelos si tienen la misma dirección, independientemente de sus sentidos.
Vectores perpendiculares: dos vectores son perpendiculares (u ortogonales) cuando sus direcciones forman un ángulo de 90º.
Vectores ortonormales: dos o más vectores son ortonormales si son perpendiculares entre sí y, además, son unitarios (su módulo es igual a la unidad).
Vectores coplanarios: dos o más vectores son coplanarios cuando están contenidos en un mismo plano.

Ángulo entre dos vectores

Para encontrar el ángulo que forman dos vectores dados, se debe aplicar la siguiente fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Donde $\lvert \vv{\text{u}} \rvert$ y $\lvert \vv{\text{v}} \rvert$ son los módulos de los vectores $\vv{\text{u}}$ y $\vv{\text{v}}$ respectivamente.

3 comentarios en “¿Qué son los vectores (matemáticas)?”

David Ballesteros Camberos
13/09/2022 a las 21:51

Por favor si se permitiera también la copia de las imágenes …. Las explicaciones son excelentes … ¡Muchas Gracias!

Responder
1. Geometría Analítica
  16/09/2022 a las 16:31
  
  Hola David,
  
  Puedes utilizar las imágenes siempre que quieras si añades un enlace al artículo del que has copiado la imagen.👍
Asbel pino
25/10/2023 a las 21:08

gracias por sus buenas explicaciones

Responder