¿Qué son las Rectas Secantes? (ejemplos)

En esta página encontrarás todo sobre las rectas secantes: qué significan, los distintos tipos que hay, cómo averiguar si dos rectas son secantes, cómo hallar su punto en común,… También podrás ver varios ejemplos y ejercicios resueltos de rectas secantes.

Índice

¿Qué son dos rectas secantes?

En matemáticas, la definición de rectas secantes es la siguiente:

Dos rectas son secantes cuando se cortan únicamente en un punto. Por lo tanto, las rectas que son secantes tienen un solo punto en común. Además, dos rectas secantes deben estar contenidas necesariamente en un mismo plano cartesiano.

Es importante el concepto de que dos rectas secantes se cruzan solamente en 1 punto, ya que si tuvieran más de un punto de corte serían rectas coincidentes y, por otro lado, si no tuvieran ningún punto de intersección se trataría de rectas paralelas.

Ejemplos de rectas secantes

Una vez hemos visto el significado de que dos rectas sean secantes, veamos ahora 2 ejemplos diferentes de este tipo de rectas:

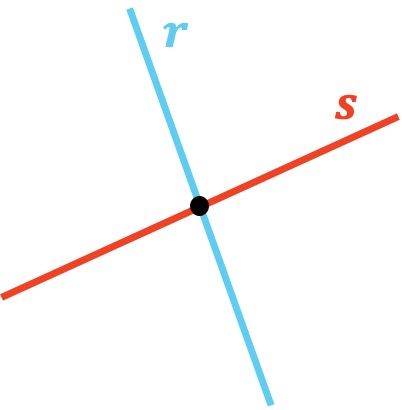
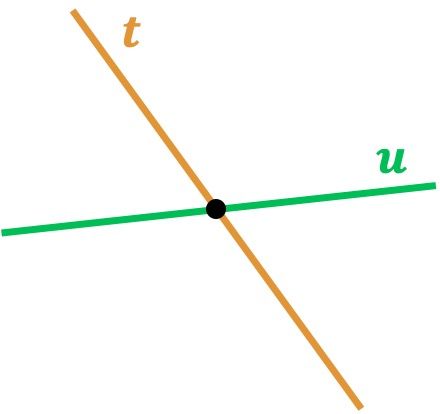
Como puedes ver, las rectas r y s son secantes entre sí porque se tocan en un punto. Y, del mismo modo, la recta t es secante con la recta u ya que hay un punto en el que se cortan.

Tipos de rectas secantes

Existen dos tipos de rectas secantes:

Rectas perpendiculares: son rectas que se cortan formando un ángulo recto de 90º.
Rectas oblicuas: consisten en rectas que se cortan formando un ángulo agudo entre 0º y 90º (no incluidos).

Rectas perpendiculares

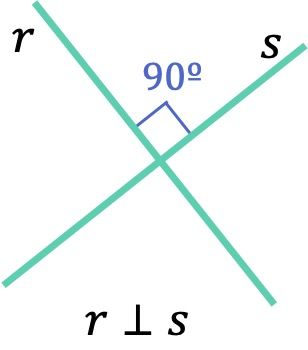
Las rectas perpendiculares son aquellas rectas secantes que se cortan formando cuatro ángulos de 90 grados.

Asimismo, las pendientes de dos rectas perpendiculares siempre cumplen la siguiente condición:

$m_r = -\cfrac{1}{m_s}$

Otra de las propiedades de las rectas secantes perpendiculares es que el producto escalar entre sus vectores directores (vector que indica la dirección de una recta) es igual a cero.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Si estás más interesad@ en las rectas perpendiculares, en este enlace puedes ver ejemplos de rectas perpendiculares. Además, también encontrarás cómo se calcula una recta perpendicular a otra, las propiedades de este tipo de rectas, ejercicios resueltos paso a paso, etc.

Rectas oblicuas

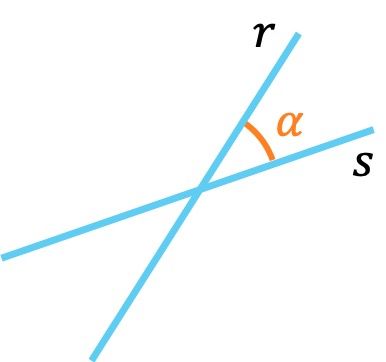
Las rectas oblicuas son aquellas rectas secantes que se intersecan formando ángulos agudos y ángulos obtusos dos a dos. Es decir, haciendo dos ángulos agudos (menores de 90º) y dos ángulos obtusos (mayores de 90º). Sin embargo, según la definición del ángulo de dos rectas, el ángulo entre dos rectas es el menor de los que forma.

Se puede calcular el ángulo entre dos rectas oblicuas con sus pendientes mediante la siguiente fórmula:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

¿Cómo saber si dos rectas son secantes?

Hay principalmente 3 métodos para encontrar la posición relativa de dos rectas:

Con los vectores directores de las dos rectas.
Con las pendientes de las dos rectas.
Con la ecuación implícita (o general) de las dos rectas.

A continuación vamos a ver la explicación los 3 métodos que existen para averiguar cuándo dos rectas son secantes.

A partir de los vectores directores de las rectas

Si las coordenadas de los vectores directores (vector que marca la dirección de una recta) de dos rectas diferentes no son proporcionales, esas dos rectas son secantes.

Veamos un ejercicio resuelto paso paso de dos rectas secantes:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Ambas rectas están expresadas en forma de ecuaciones paramétricas, de modo que las componentes del vector director de cada recta son los números de delante del parámetro $t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Entonces, para ver si los vectores directores son proporcionales debemos dividir sus coordenadas entre sí. Si en las dos divisiones obtenemos el mismo resultado serán proporcionales, por contra, si el resultado es distinto significará que los vectores no son proporcionales.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Las divisiones de las componentes no son equivalentes, por tanto, los vectores no son proporcionales y, en consecuencia, las rectas son secantes.

A partir de las pendientes

Si dos rectas tienen pendientes diferentes, implica que las rectas son secantes entre sí.

Por ejemplo, las siguientes dos rectas son secantes porque tienen una pendiente distinta:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

La pendiente de la recta $r$ es -2 y la pendiente de la recta $s$ es 3.

$m_r =-2 \neq m_s =3$

Como las dos rectas no tienen la misma pendiente, son secantes.

A partir de ecuación implícita de la recta

También se puede hallar si dos rectas son secantes o no a través de las ecuaciones implícitas (o ecuaciones generales) de las rectas. La ecuación implícita de la recta es de la siguiente forma:

$Ax+By+C=0$

Así pues, dos rectas son secantes cuando sus coeficientes A y B no son proporcionales.

Veamos un ejemplo de dos rectas secantes definidas con su ecuación implícita:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Para verificar que se trata de dos rectas secantes, debemos analizar la proporcionalidad del coeficiente A (número de delante de la variable $x$ ) con el coeficiente B (número de delante de la variable $y$ ):

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

Los dos términos no son proporcionales, por lo que efectivamente las dos rectas son secantes.

Hallar el punto en común de dos rectas secantes

Como hemos visto, las rectas que son secantes entre sí solamente tienen un punto en común. Así pues, para calcular el punto de corte de dos rectas secantes se debe resolver el sistema de ecuaciones formado por las dos rectas.

A modo de ejemplo, vamos a encontrar el punto de intersección de las siguientes dos rectas:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Para determinar el punto donde se cortan las dos rectas, debemos resolver el sistema de ecuaciones lineales formado por ambas rectas:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

En este caso, solucionaremos el sistema con el método de sustitución. Así que despejaremos la variable $x$ de la primera ecuación y la sustituiremos en la segunda ecuación:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

Y una vez sabemos cuánto vale la incógnita $y$ sustituimos su valor en la expresión hallada de $x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

De modo que la solución del sistema de ecuaciones es el punto en el que se cruzan las dos rectas. Y dicho punto es $\bm{(3,1)}.$

Recta secante a una circunferencia

Normalmente cuando decimos que dos rectas son secantes nos referimos al concepto que acabamos de ver. Sin embargo, en geometría existe otro significado de la recta secante:

Una recta secante con una circunferencia es aquella recta que corta una circunferencia (o una curva) en dos puntos diferentes.

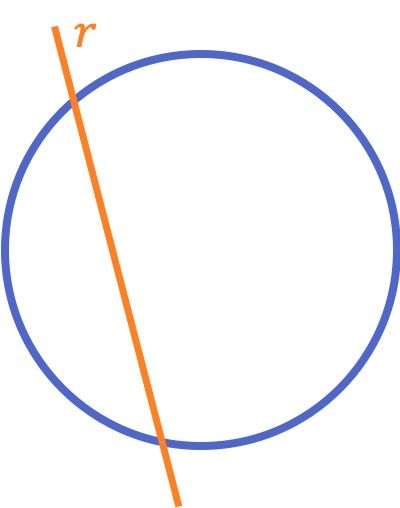
A diferencia del concepto de dos rectas secantes entre sí que se suele enseñar en primaria, frecuentemente esta definición de recta secante con una circunferencia se estudia en cursos más adelantados junto con todas las posiciones relativas de las rectas con las circunferencias.

4 comentarios en “Rectas secantes”

Micaela
07/04/2021 a las 17:23

Deterime si las rectas son secantes
r:-3x+4y-16=0
S:3x-2y+14=0

Responder
1. Geometría Analítica
  09/04/2021 a las 23:07
  
  Hola Micaela, las dos rectas están definidas en forma de ecuación implícita, por lo tanto, para resolver este ejercicio debes tener presente que dos rectas expresadas en este tipo de ecuación son secantes si los coeficientes de sus incógnitas no son proporcionales.
  
  En este caso, los coeficientes de las x tienen una relación de -1, pero la relación de proporcionalidad de los coeficientes de las y es de -2.
  $\cfrac{-3}{3}=-1\neq\cfrac{4}{-2}=-2$
  
  Como los coeficientes no son proporcionales, las dos rectas son secantes en el plano.
Estéfano
27/10/2021 a las 21:02

Como hago tres recetas secantes con dos puntos en común

Responder
1. Geometría Analítica
  29/10/2021 a las 13:14
  
  Hola Estéfano,
  
  Lo que propones no es posible, pues si dos rectas tienen dos puntos en común significa que son coincidentes.
  
  Si tienes los dos puntos, puedes hallar la ecuación de la recta (consulta nuestro post de ecuaciones de la recta) y a partir de ella obtener dos rectas con vectores múltiples y puntos diferentes. Pero seguirán siendo rectas coincidentes.