En esta página encontrarás qué son los vectores coplanarios y cómo saber si 2, 3, 4 o más vectores son coplanarios. Además, podrás ver ejemplos y ejercicios resueltos paso a paso de vectores coplanarios.
Índice
¿Qué son los vectores coplanarios?
En geometría analítica, el significado de vectores coplanarios (o coplanares) es el siguiente:
Los vectores coplanarios son aquellos vectores que pertenecen a un mismo plano.
Por lo tanto, dos vectores siempre son coplanarios porque un plano se puede formar con tan solo 2 vectores. En cambio, cuando se tienen 3, 4 o más vectores puede ser que alguno de los vectores no esté contenido en el mismo plano y, en consecuencia, que no sean coplanarios.
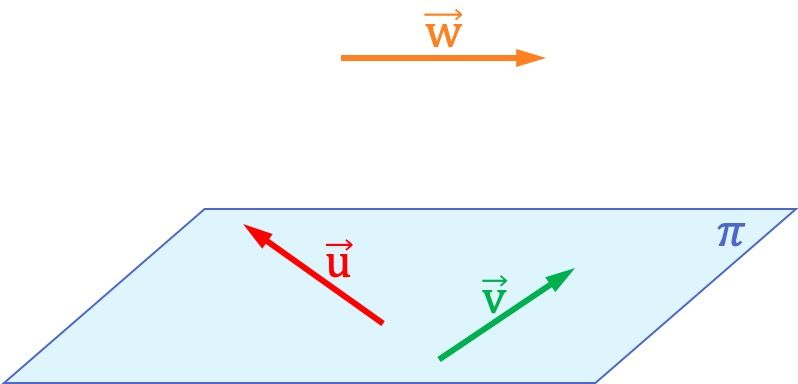
Por ejemplo, en la representación gráfica de arriba puedes ver que los vectores y
son coplanarios entre sí, ya que está contenidos en el mismo plano. Por contra, estos dos vectores no son coplanarios con el vector
, porque no se puede formar ningún plano en el espacio que contenga los tres vectores.
De esta propiedad se puede deducir que si 3 o más vectores son coplanarios, los puntos que definen dichos vectores (incio y extremo del vector) también son puntos coplanarios.
¿Cuándo los vectores son coplanarios?
Como hemos visto en la definición de vectores coplanares (o coplanarios) dos vectores siempre son coplanarios, pero más de dos vectores no tienen porqué cumplir la relación de coplanaridad.
Así pues, existen varios métodos para determinar si tres o más vectores son coplanarios:
- Si el producto mixto de tres vectores (o triple producto escalar) es igual a cero, significa que los tres vectores son coplanarios. Si no tienes muy claro cómo se calcula esta operación, te recomiendo que le eches un vistazo a qué es el producto mixto de tres vectores, aquí encontrarás la explicación junto con ejemplos y ejercicios resueltos.
- Si un conjunto de vectores se pueda expresar como combinación lineal de dos vectores implica que son coplanarios, lo que significa que 3 o más vectores son coplanarios si, y solo si, son linealmente dependientes. Para demostrar que tres o más vectores son combinación lineal de dos vectores, basta con que el rango de la matriz formada por todos los vectores sea igual a 2.
Es importante que entiendas bien el concepto de dependencia e independencia lineal, es decir, cuándo dos vectores son linealmente dependientes o linealmente independientes y qué significa. Si no lo tienes del todo claro, en el enlace encontrarás una explicación bien detallada, donde, además, podrás ver ejemplos y ejercicios resueltos paso a paso.
- Si los vectores en cuestión son vectores paralelos quiere decir que también son coplanarios, es decir, todos los vectores que son paralelos están contenidos en un mismo plano.
Ejercicios resueltos de vectores coplanarios
Ejercicio 1
Determina si los siguientes tres vectores son coplanarios:
Para verificar si se trata de 3 vectores coplanarios, debemos calcular el producto mixto entre los tres vectores:
El producto mixto de los tres vectores es nulo, por lo tanto, los 3 vectores son coplanarios.
Ejercicio 2
Encuentra si los siguientes tres vectores son coplanarios:
Una manera de comprobar si se trata de 3 vectores coplanarios sería resolver el producto mixto entre los tres vectores. Sin embargo, si nos fijamos bien en las componentes de los vectores podemos ver que son proporcionales. Por lo tanto, los tres vectores son paralelos entre sí.
Y como todos los vectores son paralelos, efectivamente se trata de 3 vectores coplanarios.
Ejercicio 3
Halla si los siguientes cuatro vectores son coplanarios:
Para hallar si los cuatro vectores son coplanarios, debemos calcular el rango de la matriz compuesta por todos los vectores:
En esta caso, calculamos el rango de dicha matriz por determinantes:
El rango de la matriz formada por todo el conjunto de los vectores es equivalente a 2, por lo que los 4 vectores son coplanarios.
Ejercicio 4
Calcula el valor del parámetro para que los siguientes 4 puntos sean coplanarios:
Para que los cuatro puntos sean coplanarios, los vectores que quedan determinados por ellos deben ser coplanarios. De modo que calculamos dichos vectores:
Cuya matriz de vectores es:
Para que los vectores resultantes sean coplanarios, el rango de la matriz debe ser 2. Y, por tanto, el determinante de toda la matriz 3×3 tiene que ser igual a 0:
Finalmente, despejamos la incógnita
