Vectores paralelos

En esta página encontrarás todo sobre los vectores paralelos: qué significan, cuándo dos vectores son paralelos, cómo hallar un vector paralelo a otro vector, las propiedades de este tipo de vectores,… Además, podrás ver varios ejemplos y ejercicios resueltos de vectores paralelos.

¿Qué son los vectores paralelos?

Los vectores paralelos son aquellos vectores que tienen la misma dirección. Es decir, dos vectores son paralelos si están contenidos dentro de dos rectas paralelas. Por lo tanto, dos vectores paralelos forman entre ellos un ángulo de 0 o 180 grados.

Por ejemplo, los siguientes tres vectores son paralelos:

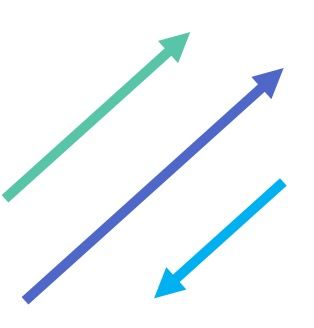
Además, el paralelismo de dos vectores solo depende de su dirección. Es decir, dos vectores serán paralelos si coinciden en la dirección, independientemente de si tienen el mismo sentido o el sentido contrario. Y lo mismo sucede con el módulo (o magnitud), dos vectores pueden tener diferente módulo y ser paralelos.

Por otro lado, cuando dos vectores tienen la misma dirección pero sentido opuesto se llaman vectores antiparalelos.

¿Cómo se sabe cuándo dos vectores son paralelos?

Dos vectores son paralelos cuando son proporcionales. Por tanto, para hallar si dos vectores son paralelos se debe determinar si sus respectivas componentes son proporcionales o no.

Vamos a ver cómo saber si dos vectores son paralelos mediante dos ejercicios resueltos diferentes, uno con vectores de 2 coordenadas y el otro con vectores de 3 coordenadas.

Ejemplo de vectores paralelos en el plano (en R2)

• Determina si los siguientes dos vectores son paralelos:

Para averiguar si realmente son vectores paralelos debemos ver si sus coordenadas cartesianas son proporcionales:

Al dividir las componentes X y las componentes Y entre sí obtenemos el mismo resultado (-2), por lo que los dos vectores son proporcionales y, en consecuencia, también son paralelos.

Fíjate que en matemáticas cuando dos elementos geométricos son paralelos se indica con dos barras verticales (II).

Ejemplo de vectores paralelos en el espacio (en R3)

• Encuentra si se cumple la condición de paralelismo en los siguientes dos vectores:

Para determinar si realmente se trata de vectores paralelos debemos verificar si las coordenadas de los vectores son proporcionales:

Las componentes X y las componentes Y de los vectores sí que son proporcionales entre sí porque al dividirlas conseguimos el mismo resultado, en cambio, no son proporcionales con la componente Z. Por lo tanto, los vectores no son proporcionales del todo y, en consecuencia, no son paralelos.

¿Cómo calcular un vector paralelo?

Para hallar un vector paralelo a otro vector es suficiente en multiplicarlo por un escalar (un número real) diferente de cero (0). De modo que existen infinitos vectores paralelos entre sí, ya que el vector se puede multiplicar por infinitos números.

Por ejemplo, vamos a calcular varios vectores paralelos del siguiente vector:

El resultado de todos los siguientes productos son vectores paralelos al vector anterior:

Propiedades de los vectores paralelos

Los vectores paralelos tienen las siguientes características:

• Propiedad reflexiva: todo vector es paralelo a sí mismo.

• Propiedad simétrica: si un vector es paralelo a otro, aquel vector también es paralelo al primero. Esta propiedad también la poseen los vectores perpendiculares.

• Propiedad transitiva: si un vector es paralelo a otro vector, y este segundo vector es a la vez paralelo a un tercer vector, el primer vector también es paralelo al tercer vector.

• El producto escalar de dos vectores paralelos es igual al producto de sus módulos. Puedes comprobar por qué sucede esto tan peculiar en las propiedades del producto escalar.

• Dos vectores paralelos siempre son linealmente dependientes. Este concepto es bastante importante, así que si no estás familiarizado con él puedes consultar qué son dos vectores linealmente dependientes.