▷ ¿Qué es una Combinación Lineal de Vectores? (con ejemplos)

En esta página encontrarás la explicación de qué significa una combinación lineal entre vectores. También, podrás ver un ejemplo de cómo se expresa un vector en forma de combinación lineal y, además, podrás practicar con ejercicios y problemas resueltos paso a paso.

Índice

¿Qué es la combinación lineal de vectores?

La definición de combinación lineal es la siguiente:

Una combinación lineal de un conjunto de vectores es el vector que se obtiene al sumar todos los vectores del conjunto multiplicados por escalares (números reales).

Es decir, dado un conjunto de vectores $\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$ una combinación lineal de ellos sería:

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

Donde los coeficientes $a_i$ son números reales.

Por lo tanto, un vector que es combinación lineal de otros vectores significa que el primero se puede expresar en función de los segundos.

Este concepto se puede entender mejor representando gráficamente en el plano un vector que sea combinación lineal de dos vectores:

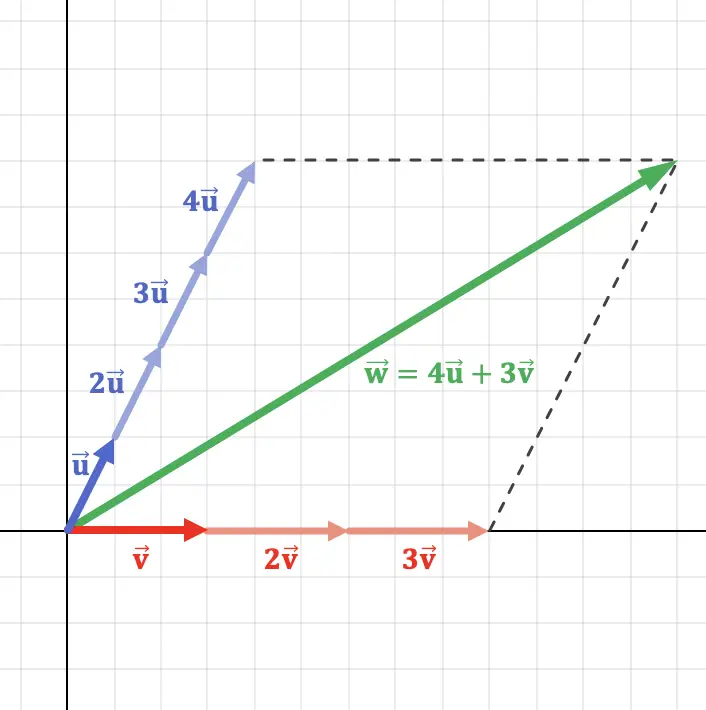
Com puedes ver en la representación gráfica anterior, el vector $\vv{\text{w}}$ se puede obtener a partir de los vectores $\vv{\text{u}}$ y $\vv{\text{v}}$ haciendo operaciones vectoriales. Por lo tanto, el vector $\vv{\text{w}}$ es una combinación lineal de los otros dos vectores.

Hay que recalcar que esta combinación lineal es única, o dicho con otras palabras, solamente existe una combinación lineal factible para cada vector. Ya que, siguiendo el ejemplo anterior, si multiplicáramos $\vv{\text{u}}$ por 6 en vez de por 4, estaríamos obteniendo otro vector diferente.

Además, una de las propiedades de la combinación lineal en el plano (en R2) es que cualquier vector se puede poner como combinación lineal de otros dos vectores si estos tienen distinta dirección, es decir, si no son paralelos.

A parte, a veces se puede identificar a simple vista que dos vectores son combinación lineal. Para ello, basta que sus componentes sean proporcionales. Por ejemplo, las coordenadas de los siguientes dos vectores son proporcionales y, en consecuencia, los vectores son combinación lineal:

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Finalmente, ya sea en un espacio vectorial bidimensional (en R2) o tridimensional (en R3), si existe alguna combinación lineal dentro de un conjunto de vectores implica que estos son linealmente dependientes entre sí. En cambio, si no es posible ninguna combinación lineal entre los vectores, quiere decir que son linealmente independientes.

Si no te ha quedado del todo claro el último concepto, te recomendamos que consultes nuestra explicación sobre los vectores linealmente dependientes e independientes, aquí encontrarás qué significa que los vectores sean linealmente dependientes o independientes, ejemplos de cada tipo y las diferencias entre ellos. Este concepto se utiliza mucho y, de hecho, se suele preguntar en los exámenes, por lo que es importante que lo entiendas bien.

Cómo expresar un vector como combinación lineal de otros vectores

A continuación vamos a ver cómo se resuelve un problema típico en el que nos piden encontrar la combinación lineal de un vector.

Expresa el vector $\vv{\text{x}}$ como combinación lineal de $\vv{\text{u}}, \vv{\text{v}}$ y $\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

Para que el vector $\vv{\text{x}}$ sea combinación lineal de los otros vectores se debe cumplir la siguiente ecuación:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Donde los coeficientes $a_1, a_2$ y $a_3$ son las incógnitas que debemos hallar.

Así que sustituimos cada vector por sus coordenadas:

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

Multiplicamos cada vector por su coeficiente:

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

Hacemos la suma de vectores:

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

Cada coordenada de la izquierda tiene que ser igual a cada coordenada de la derecha. Por lo tanto, tenemos 3 ecuaciones:

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

De modo que lo único que debemos hacer es resolver el sistema de ecuaciones obtenido. Para ello, pues utilizar el método que prefieras (método de sustitución, regla de Cramer, método de Gauss-Jordan,…), nosotros en este caso usaremos el método de Gauss:

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

De manera que el sistema escalonado obtenido es:

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

Ahora solo nos queda despejar las incógnitas y hallar su valor. Así que de la última ecuación encontramos $a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

De la segunda ecuación del sistema calculamos el valor de $a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

Y, finalmente, de la primera ecuación del sistema escalonado hallamos la incógnita $a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

Por lo tanto, la solución del sistema de ecuaciones lineales es:

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

De manera que el vector $\vv{\text{x}}$ se puede expresar mediante la siguiente combinación lineal:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

Así pues, efectivamente existe una dependencia lineal entre los vectores. Por contra, si no hubiésemos obtenido ninguna solución del sistema de ecuaciones, significaría que el vector $\vv{\text{x}}$ tiene independencia lineal respecto a los otros vectores y, por tanto, no existiría ninguna combinación lineal posible para obtener dicho vector a partir de los otros vectores.

Ejercicios resueltos de combinación lineal de vectores

Ejercicio 1

De los tres vectores siguientes, indica qué parejas son combinación lineal entre sí. Además, encuentra la relación de combinación lineal de dichas parejas de vectores.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

Ver solución

Para saber si una pareja de vectores son combinación lineal tenemos que ver si sus coordenadas son proporcionales.

Primero comprobamos el vector $\vv{\text{u}}$ con el vector $\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

En segundo lugar, verificamos el vector $\vv{\text{u}}$ con el vector $\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

Finalmente, probamos el vector $\vv{\text{v}}$ junto con el vector $\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

De manera que la única pareja de vectores que son combinación lineal son $\vv{\text{v}}$ y $\vv{\text{w}}.$ Además, su relación es la siguiente:

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

O equivalentemente:

$\vv{\text{w}}= -3 \vv{\text{v}}$

Aunque no lo pedía el enunciado, los únicos vectores linealmente dependientes entre sí son $\vv{\text{v}}$ y $\vv{\text{w}}$ porque existe una combinación lineal entre ellos. El resto de parejas son linealmente independientes, ya que no se pueden combinar linealmente.

Ejercicio 2

Encuentra la relación lineal entre el vector $\vv{\text{x}}$ y el conjunto de vectores $\vv{\text{u}}, \vv{\text{v}}$ y $\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

Ver solución

Para que el vector $\vv{\text{x}}$ sea combinación lineal de los otros vectores se debe cumplir la siguiente ecuación:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Así que sustituimos cada vector por sus coordenadas:

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

Multiplicamos cada vector por su constante:

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

Sumamos los vectores:

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

De modo que obtenemos el siguiente sistema de ecuaciones:

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

Resolvemos el sistema obtenido mediante el método de Gauss:

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

De manera que el sistema escalonado obtenido es:

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

Ahora solo nos queda despejar las incógnitas y hallar su valor. Así que de la última ecuación encontramos $a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

De la segunda ecuación del sistema calculamos el valor de $a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

Y, por último, de la primera ecuación del sistema escalonado hallamos la incógnita $a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

Por lo tanto, la solución del sistema de ecuaciones lineales es:

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

De manera que el vector $\vv{\text{x}}$ se puede expresar mediante la siguiente combinación lineal:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

Ejercicio 3

Expresa el vector $\vv{\text{x}}$ como combinación lineal de los vectores $\vv{\text{u}}, \vv{\text{v}}$ y $\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

Ver solución

Planteamos la ecuación de combinación lineal respecto el vector $\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Así que sustituimos cada vector por sus componentes:

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

Multiplicamos cada vector por su respectiva incógnita:

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

Realizamos la suma de vectores:

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

De modo que hemos obtenido el siguiente sistema de ecuaciones:

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

Resolvemos el sistema obtenido mediante el método de Gauss:

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

De manera que el sistema escalonado obtenido es:

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

Ahora solo nos queda despejar las incógnitas y hallar su valor. Así que de la última ecuación encontramos $a_3:$

$a_3 = -4$

De la segunda ecuación del sistema hallamos el valor de $a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

Y, para terminar, de la primera ecuación del sistema escalonado despejamos la incógnita $a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

Por lo tanto, la solución del sistema de ecuaciones lineales es:

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

De modo que el vector $\vv{\text{x}}$ se puede expresar combinando linealmente los otros vectores:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

Ejercicio 4

Determina si el vector $\vv{\text{x}}$ se puede expresar en forma de combinación lineal a partir de los vectores $\vv{\text{u}}, \vv{\text{v}}$ y $\vv{\text{w}}.$ En cuyo caso, halla la expresión que los relaciona.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

Ver solución

Para que el vector $\vv{\text{x}}$ sea combinación lineal de los otros vectores se tiene que cumplir la siguiente ecuación:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Así que sustituimos cada vector por sus coordenadas:

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

Multiplicamos cada vector por su coeficiente:

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

Sumamos los vectores:

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

De modo que la expresión anterior es equivalente al siguiente sistema de ecuaciones:

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

Ahora resolvemos el sistema obtenido mediante el método de Gauss:

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

De manera que hemos obtenido el siguiente sistema de ecuaciones:

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

Sin embargo, la última ecuación nunca se podrá cumplir, ya que 0 nunca será igual a -30 independientemente de los valores que tomen las incógnitas. Por lo tanto, el sistema no tiene solución y esto implica que no existe ninguna combinación lineal que nos permita calcular el vector $\vv{\text{x}}.$

Combinación lineal de vectores

¿Qué es la combinación lineal de vectores?

Cómo expresar un vector como combinación lineal de otros vectores

Ejercicios resueltos de combinación lineal de vectores

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

1 comentario en “Combinación lineal de vectores”

Deja un comentario Cancelar respuesta