▷ ¿Qué son las Rectas Paralelas? (ejemplos)

Aquí encontrarás todo sobre las recta paralelas: qué significan, cómo determinar si dos rectas son paralelas, sus propiedades,… Además, podrás ver varios ejemplos y ejercicios resueltos de rectas paralelas.

Índice

¿Qué son las rectas paralelas?

Las rectas paralelas son aquellas líneas que nunca se cortan, es decir, aunque se prolongue sus trayectorias hasta el infinito nunca llegan a tocarse. Por lo tanto, los puntos de dos rectas paralelas siempre están a una misma distancia entre sí y, además, dos rectas paralelas no tienen ningún punto en común.

Por ejemplo, las siguientes dos rectas son paralelas:

Se suele indicar que dos rectas son paralelas con 2 barras verticales || entre las rectas.

Por otro lado, a pesar de que dos rectas paralelas nunca se cruzan, en geometría analítica se dice que forman un ángulo de 0º ya que tienen la misma dirección.

¿Cuándo dos rectas son paralelas?

Una vez vista la definición de rectas paralelas, vamos a ver cómo hallar dos rectas paralelas. Evidentemente, una manera sería representar las rectas gráficamente y ver si se cruzan en la gráfica, pero hay métodos incluso más sencillos y más fáciles de utilizar.

Determinar el paralelismo de dos rectas con sus pendientes

Se puede saber cuándo dos rectas son paralelas a partir de la pendiente de cada recta. Recuerda que la pendiente de una recta es el parámetro $m$ de la ecuación explícita y de la ecuación punto-pendiente de la recta:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Sin embargo, existen varias formas de determinar la pendiente de una recta, así que para saber cómo se calcula te recomendamos que le eches un vistazo a la fórmula de la pendiente de una recta. Además, en la página del enlace también encontrarás la explicación de qué representa la pendiente de una recta y por qué es tan importante para una recta.

Así pues, en el plano, dos rectas son paralelas si tienen la misma pendiente (coeficiente m) y diferente ordenada en el origen (coeficiente n).

Por ejemplo, las siguientes dos rectas son paralelas:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

Se trata de dos rectas paralelas porque ambas tienen la misma pendiente y, además, sus términos independientes son distintos.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

Cabe destacar que si dos rectas tuvieran la misma pendiente y a la vez la misma ordenada en el origen, serían rectas coincidentes porque serían exactamente idénticas.

Hallar el paralelismo de dos rectas a partir de la ecuación implícita

Recordemos que la ecuación implícita (o general) de la recta es:

$Ax+By+C=0$

Entonces, si los coeficientes A y B de dos rectas son proporcionales entre sí pero no con el coeficiente C, significa que las rectas son paralelas.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

A continuación tienes dos rectas paralelas expresadas en forma de ecuación general (o implícita):

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

Son paralelas por que los números de delante de la variable $x$ son proporcionales con los números de delante de la variable $y$ , pero no con los términos independientes.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

Al igual que antes, si todos los coeficientes (A, B y C) de dos rectas implícitas fuesen proporcionales, implicaría que las dos rectas son coincidentes, o dicho con otras palabras, que son iguales.

Propiedades de las rectas paralelas

Las características de las rectas paralelas son las siguientes:

Propiedad simétrica: si una recta es paralela a otra, aquella recta también es paralela a la primera. Esta propiedad también la poseen las rectas perpendiculares.

$r \parallel s \ \longrightarrow \ s \parallel r$

Propiedad transitiva: si una recta es paralela a otra recta, y esta segunda recta es a la vez paralela a una tercera recta, la primera recta también es paralela a la tercera recta.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

El producto escalar de los vectores directores (vector que indica la dirección de una recta) de dos rectas paralelas es igual al producto de sus módulos.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

Además, los vectores directores de dos rectas paralelas siempre son linealmente dependientes entre sí, ya que son proporcionales.

Esta condición es necesaria para ser rectas paralelas pero no suficiente, o dicho de otra forma, dos rectas paralelas deben tener vectores directores proporcionales, pero que dos rectas tengan vectores directores proporcionales no implica directamente que estas sean paralelas. Ya que las rectas coincidentes también tienen vectores directores proporcionales.

Las rectas paralelas al eje de las abscisas (eje X) son horizontales y siempre son de la forma $y=k.$

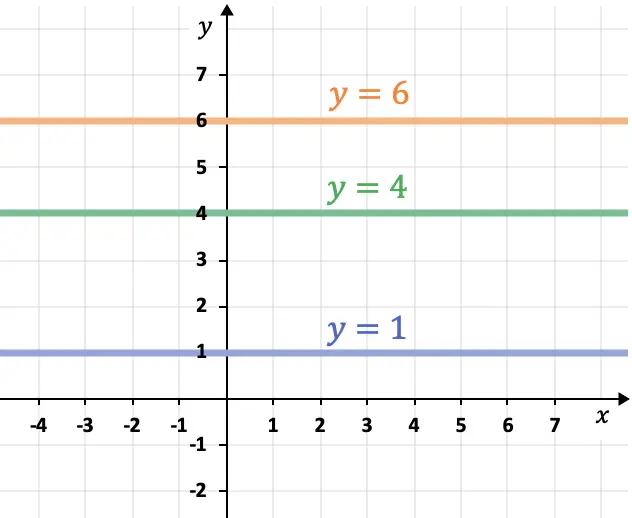
Las rectas paralelas al eje de las ordenadas (eje Y) son verticales y siempre siguen la expresión $x=k.$

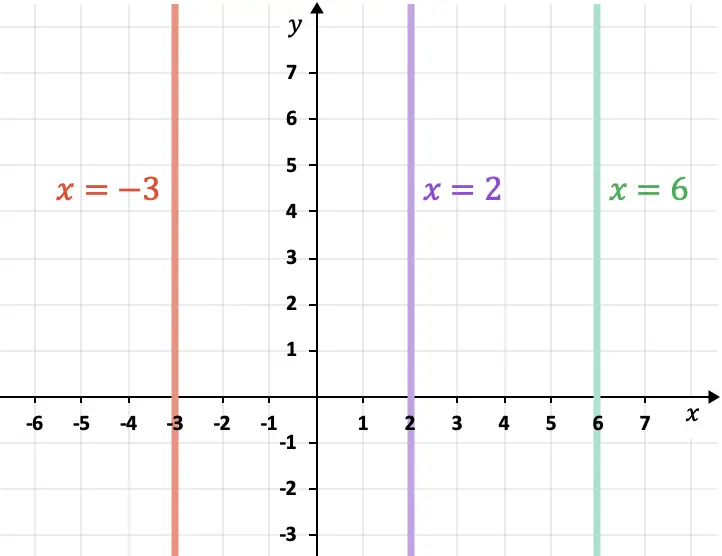
Cómo calcular la distancia entre dos rectas paralelas en el plano

Para hallar la distancia entre dos rectas paralelas en el plano (en R2), solo tenemos que coger un punto de cualquiera de las dos rectas y calcular la distancia que hay desde ese punto hasta la otra recta.

Lo podemos hacer de esta manera porque dos rectas paralelas siempre están a una misma distancia entre ellas.

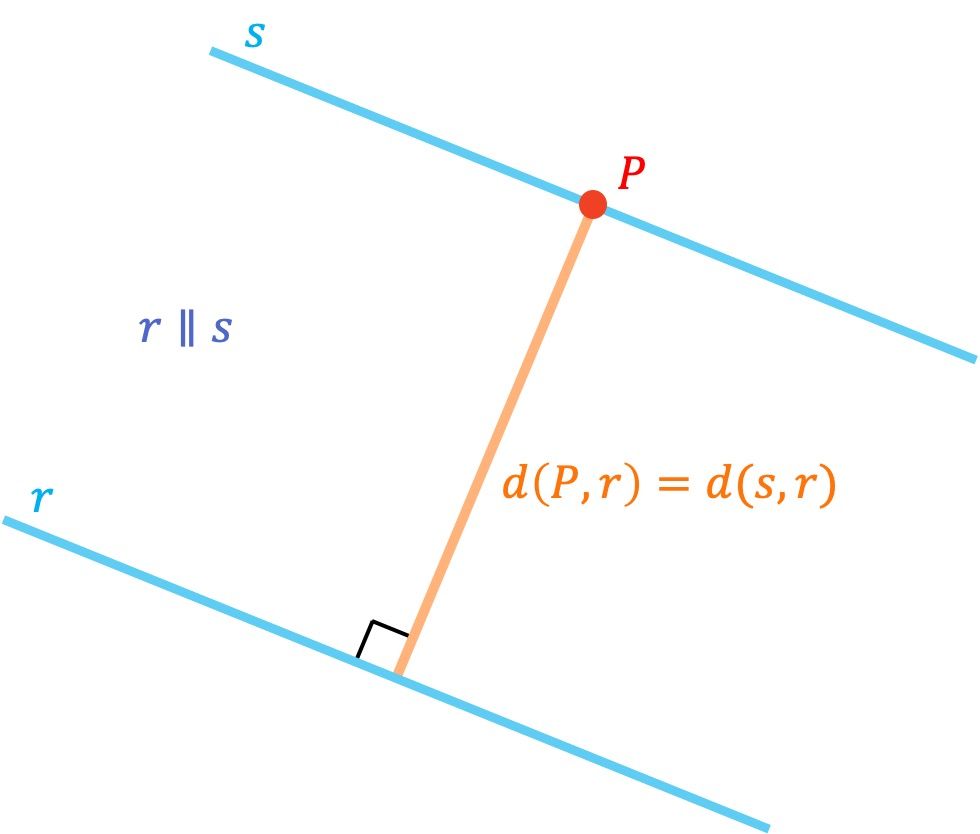
Por otro lado, si al usar la fórmula obtenemos una distancia de 0 unidades, significa que las rectas se tocan en algún punto y, por tanto, las rectas no son paralelas, sino que son secantes, coincidentes o perpendiculares. Si quieres puedes consultar las diferencias entre este tipo de rectas en nuestra web.

Así pues, para que puedas ver cómo se hace, vamos a determinar la distancia entre las siguientes dos rectas paralelas a modo de ejemplo:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Lo primero que debemos hacer es conseguir un punto de una de las rectas (la que quieras). En este caso calcularemos un punto de la recta $s.$ Para ello, tenemos que dar un valor a una de las variables, nosotros haremos por ejemplo $x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Y ahora despejamos la otra variable ( $y$ ) de la ecuación obtenida para saber cuánto vale en este punto:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Por tanto, el punto obtenido de la recta $s$ es:

$P(0,-2)$

Y una vez ya tenemos un punto de una recta, calculamos la distancia desde ese punto hasta la otra recta mediante la fórmula de la distancia de un punto a una recta:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

De forma que la distancia entre las dos rectas paralelas es equivalente a 0,45 unidades.

Ejercicios resueltos de rectas paralelas

Ejercicio 1

¿Cuáles de las siguientes rectas son paralelas?

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

Ver solución

Dos rectas son paralelas sí tienen la misma pendiente (y diferente ordenada en el origen). Así pues, la pendiente de cada recta es:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

Por tanto, solamente son paralelas las rectas $r$ y $q,$ porque son las únicas con pendientes iguales.

Ejercicio 2

Encuentra la ecuación explícita de la recta paralela a la recta $r$ y que pasa por el punto $P(0,2).$ Siendo la recta $r:$

$r: \; y=3x-1$

Ver solución

Para que la recta sea paralela a la recta $r,$ ambas deben tener la misma pendiente. Y la pendiente de la recta $r$ es 3:

$m = 3$

Por tanto, la ecuación explícita de la recta que debemos hallar será de la siguiente forma:

$y=3x+n$

Y una vez sabemos la pendiente de la recta, podemos calcular la ordenada en el origen sustituyendo el punto que pertenece a la recta en la ecuación de la recta:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

Por lo que la ecuación explícita de la recta es:

$\bm{y=3x+2}$

Ejercicio 3

Calcula el valor de las incógnitas $a$ y $b$ para que las siguientes dos rectas sean paralelas:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

Ver solución

Las rectas están descritas en forma de ecuación general (o implícita). Por tanto, para que las dos rectas sean paralelas, sus coeficientes A y B deben ser proporcionales, o dicho de otra forma, se debe cumplir la siguiente ecuación:

$\cfrac{2}{1} = \cfrac{-4}{a}$

Así que debemos resolver la ecuación anterior para obtener el valor de la incógnita $a.$ Para ello, multiplicamos las fracciones en cruz:

$2 \cdot a = -4 \cdot 1$

$a = \cfrac{-4}{2}$

$\bm{a=-2}$

Por otro lado, para que las rectas sean paralelas sus términos independientes no pueden ser proporcionales con los otros coeficientes:

$\cfrac{2}{1} \neq \cfrac{6}{b}$

Por tanto, al igual que antes, resolvemos la inecuación multiplicando las fracciones en cruz:

$2 \cdot b \neq 6 \cdot 1$

$b \neq \cfrac{6}{2}$

$\bm{b\neq 3}$

En definitiva, para que las dos rectas sean paralelas $a$ debe ser 2 y $b$ puede ser cualquier número real menos 3.

Ejercicio 4

¿Cuál es la distancia entre las siguientes dos rectas paralelas?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

Ver solución

Antes de nada, vamos a comprobar que sean dos rectas paralelas. Para ello, los coeficientes de las variables $x$ e $y$ deben ser proporcionales entre sí pero no con los términos independientes:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

Efectivamente, las rectas son paralelas, así que podemos aplicar el procedimiento.

Ahora debemos conseguir un punto de una de las rectas (la que quieras). En este caso calcularemos un punto de la recta $s.$ Para ello tenemos que otorgar un valor a una de las variables, nosotros haremos por ejemplo $x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$