En esta página encontrarás la explicación de todo sobre la geometría analítica en el espacio (y las fórmulas): ecuaciones de la recta y del plano, posiciones relativas entre planos y rectas, cómo se calculan las distancias y los ángulos en el espacio,…
Índice
¿Qué es la geometría en el espacio?
La geometría del espacio es la rama de la geometría que se encarga de estudiar las figuras geométricas que tienen tres dimensiones (3D), es decir, que ocupan un lugar en el espacio. Como por ejemplo, el cono, el cubo, la pirámide, la esfera, el cilindro, los prismas, los poliedros, etc.
Sin embargo, en esta página nos centraremos en la geometría analítica en el espacio, la parte de la geometría del espacio que se centra en analizar los puntos, las rectas, los planos, las distancias entre dos figuras geométricas, el ángulo que forman, los puntos de intersección entre diferentes elementos geométricos, etc.
Ecuaciones de la recta en el espacio
Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.
Así pues, para expresar matemáticamente cualquier recta en un espacio tridimensional (en R3) se utilizan las ecuaciones de la recta, y para hallarlas únicamente se necesita un punto que pertenezca a la recta y el vector director de dicha recta.
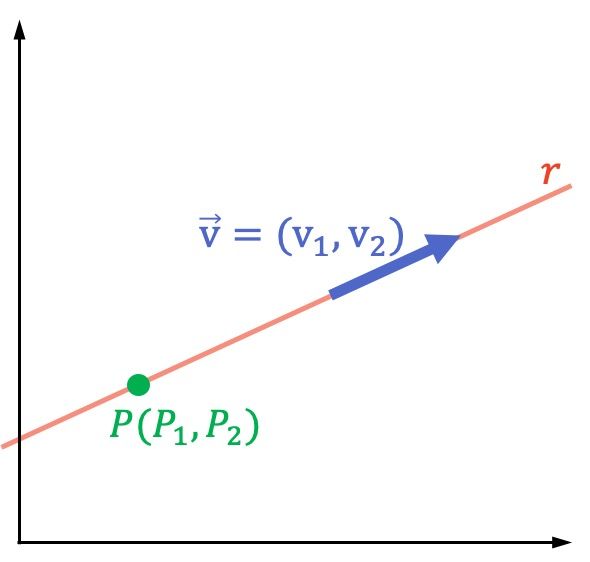
Con tan solo estos dos elementos geométricos se pueden encontrar absolutamente todas las distintas ecuaciones de la recta, que son las siguientes:
Las ecuaciones de la recta son la ecuación vectorial, las ecuaciones paramétricas, la ecuación continua y la ecuación implícita (o general).
A continuación tienes una explicación de los distintos tipos de ecuaciones de la recta.
Ecuación vectorial de la recta en el espacio
Si es el vector director de la recta y
un punto que pertenece a la recta:
La fórmula de la ecuación vectorial de la recta es:
Ecuaciones paramétricas de la recta en el espacio
Podemos obtener la fórmula de la ecuación paramétrica de una recta a partir de su ecuación vectorial igualando componente a componente:
Ecuación continua de la recta en el espacio
La fórmula de la ecuación continua de la recta es:
Este tipo de ecuación de la recta también se puede obtener a partir de las ecuaciones paramétricas, puedes ver la demostración en nuestra página de la ecuación continua, además, también podrás ver ejemplos y practicar con ejercicios resueltos de las ecuaciones de la recta.
Ecuaciones general (o implícita) de la recta en el espacio
Finalmente, multiplicando dos a dos las fracciones de la ecuación continua de la recta se consiguen las ecuaciones generales (o implícitas) de la recta:
Este tipo de ecuación de la recta también se llama ecuación cartesiana.
Acabamos de ver las 4 ecuaciones de la recta más relevantes (vectorial, paramétrica, continua y general), sin embargo, existe otra ecuación que es un poco peculiar y, por tanto, se necesita toda una página para explicarla. Se trata de la ecuación canónica, en este enlace podrás ver toda su explicación, por qué es tan especial y qué la hace diferente a todas las demás.
Ecuaciones del plano en el espacio
En geometría analítica, la ecuación de un plano es una ecuación que permite expresar analíticamente cualquier plano. De modo que para hallar la ecuación de un plano solo se necesita un punto y dos vectores linealmente independientes que pertenezcan a dicho plano.
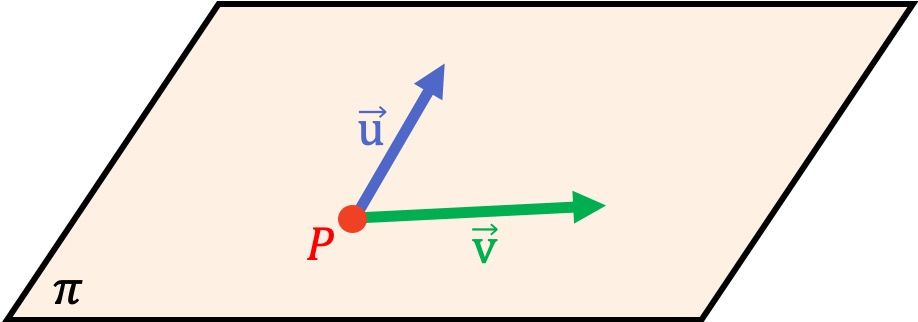
Así pues, todos los tipos de ecuaciones del plano son: la ecuación vectorial, las ecuaciones paramétricas, la ecuación implícita (o general) y la ecuación canónica (o segmentaria) del plano.
A continuación vamos a ver la explicación y la fórmula de todas las ecuaciones del plano.
Ecuación vectorial del plano
Dados un punto y dos vectores directores de un plano:
La fórmula de la ecuación vectorial de un plano es:
O, equivalentemente:
Donde y
son dos escalares, es decir, dos números reales.
Ecuaciones paramétricas del plano
Por otro lado, la fórmula de la ecuación paramétrica del plano es:
Ecuación implícita o general del plano
La ecuación implícita de un plano, también llamada ecuación general, se obtiene resolviendo el siguiente determinante e igualando el resultado a 0:
De modo que la ecuación implícita o general del plano resultante será de la siguiente forma:
Este tipo de ecuación del plano también se llama ecuación cartesiana del plano.
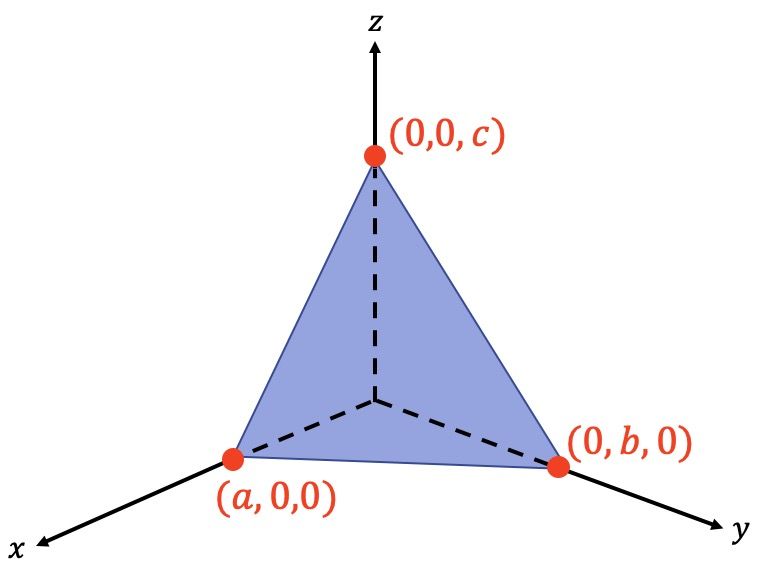
Ecuación canónica o segmentaria del plano
La fórmula de la ecuación canónica o segmentaria de un plano es la siguiente:
Donde:
es el punto de intersección entre el plano y el eje X.
es el punto de corte entre el plano y el eje Y.
es donde se cortan el plano con el eje Z.
Vector normal a un plano
El vector normal a un plano es un vector que es perpendicular a todas las rectas que están contenidas en ese plano. Por lo tanto, un vector normal a un plano significa que es perpendicular al plano.
Muchos problemas métricos de geometría analítica en el espacio son sobre los planos y sus vectores normales. Para poder resolver estos ejercicios simplemente debes saber la relación matemática que hay entre un plano y su vector normal:
Las componentes X, Y, Z del vector normal a un plano coinciden respectivamente con los coeficientes A, B, C de la ecuación implícita (o general) de dicho plano.
Donde es el vector ortogonal al plano
Posiciones relativas de dos elementos geométricos en el espacio
Evidentemente, una recta o un plano no tienen porqué estar solos en el espacio, sino todo lo contrario, normalmente interactúan entre ellos: se cortan, son paralelos, perpendiculares, etc. Pues en este apartado veremos las diferentes posiciones relativas de las rectas y de los planos y cómo se determinan.
Posición relativa de dos rectas en el espacio
En geometría analítica, cuando trabajamos en un espacio tridimensional (en R3) existen 4 posibles posiciones relativas entre dos rectas: dos rectas pueden ser rectas coincidentes, rectas paralelas, rectas secantes o rectas que se cruzan.
Rectas paralelas
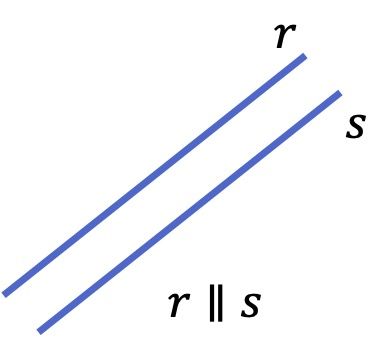
Dos rectas son paralelas si tienen la misma dirección pero no tienen ningún punto en común. A parte, las rectas paralelas siempre están a una misma distancia entre sí.
Rectas coincidentes

Dos rectas son coincidentes si tienen la misma dirección y, además, todos sus puntos son comunes.
Rectas secantes
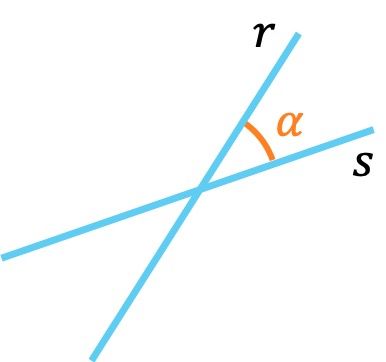
Dos rectas secantes tienen diferente dirección pero se tocan en un punto.
Rectas que se cruzan
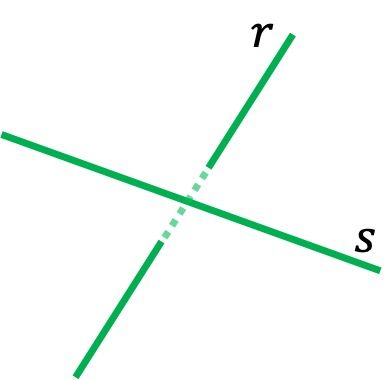
Dos rectas que se cruzan tienen distinta dirección y no se intersecan en ningún punto. Por lo tanto, dos rectas cruzadas no están en el mismo plano. Por ejemplo, en la representación gráfica de arriba la recta siempre está delante de la recta
, por lo que nunca se tocarán entre sí.
Cómo hallar la posición relativa de dos rectas por rangos
Una forma de encontrar la posición relativa de dos rectas es calculando los rangos de dos matrices concretas, como veremos a continuación. Este método es muy útil cuando ambas rectas están expresadas en forma de ecuación implícita (o general).
De manera que, si tenemos dos rectas expresadas con sus ecuaciones implícitas (o generales) en un espacio de tres dimensiones (en R3):
Sea A la matriz compuesta por los coeficientes de las dos rectas:
Y dada la matriz ampliada A’ que es la matriz formada por todos los parámetros de las dos rectas:
Entonces, la posición relativa de las dos rectas puede ser determinada por el rango de las dos matrices anteriores según la siguiente tabla:
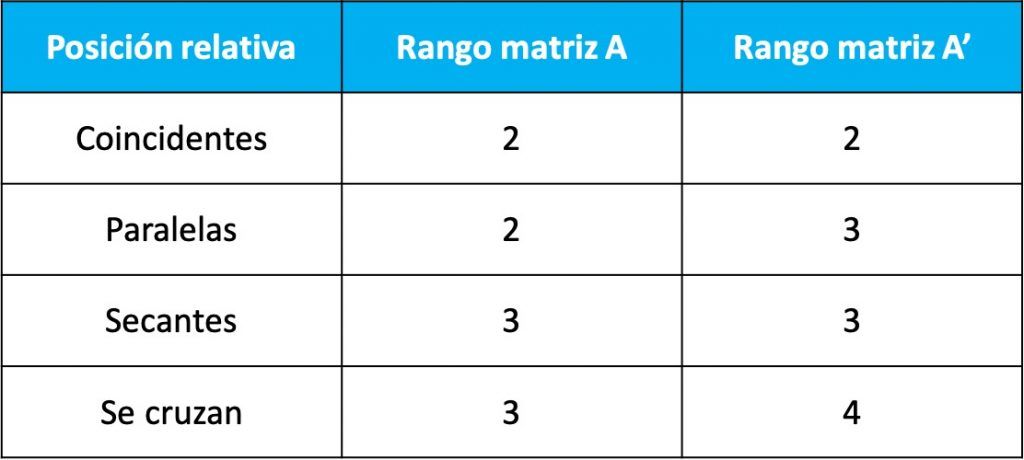
Por tanto, para encontrar la posición relativa entre dos rectas tendremos que calcular los rangos de las dos matrices y según el rango de cada matriz se tratará de un caso u otro.
Este teorema se puede demostrar a partir del teorema de Rouché-Frobenius (un método que sirve para resolver sistemas de ecuaciones lineales), sin embargo en esta página no haremos la demostración porque es bastante engorrosa y no aporta demasiado.
Posición relativa de dos planos en el espacio
En geometría analítica, solo existen tres posibles posiciones relativas entre dos planos: planos secantes, planos paralelos y planos coincidentes.
- Planos secantes: dos planos son secantes si solo se cortan en una recta.
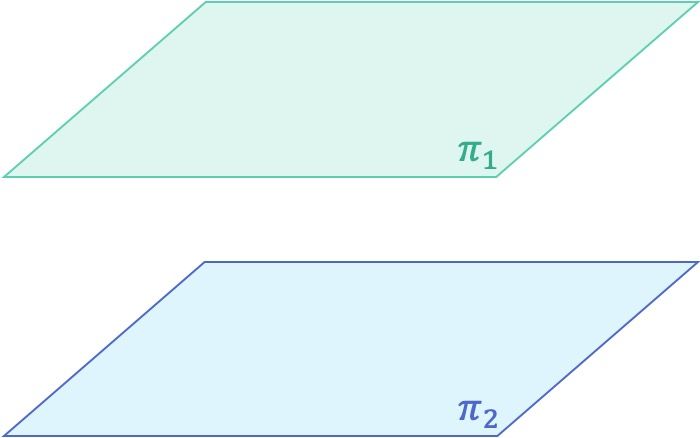
- Planos paralelos: dos planos son paralelos si no se cruzan en ningún punto.
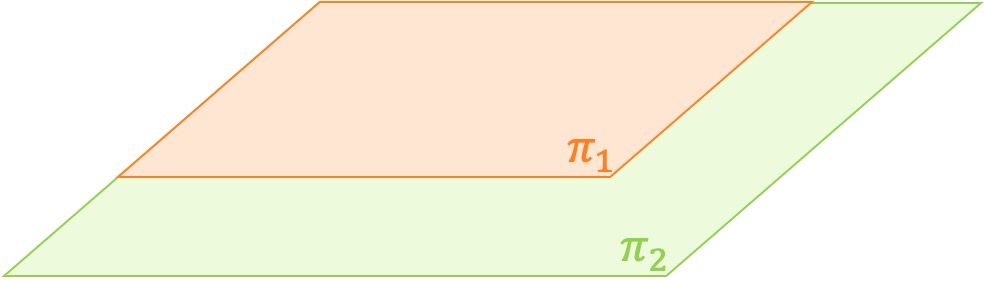
- Planos coincidentes: dos planos son coincidentes si tienen todos los puntos en común.
Planos secantes
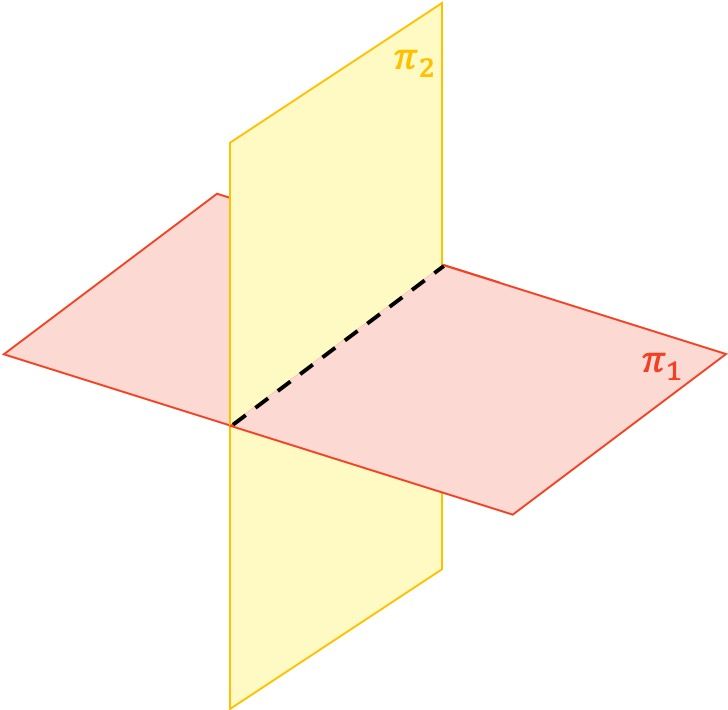
Planos paralelos
Planos coincidentes
Cómo determinar la posición relativa de dos planos por coeficientes
Una manera de averiguar cuál es la posición relativa entre dos planos es a través de los coeficientes de sus ecuaciones generales (o implícitas).
Entonces, sea la ecuación general (o implícita) de dos planos diferentes:
La posición relativa entre los dos planos en un espacio de 3 dimensiones depende de la proporcionalidad de sus coeficientes o parámetros:
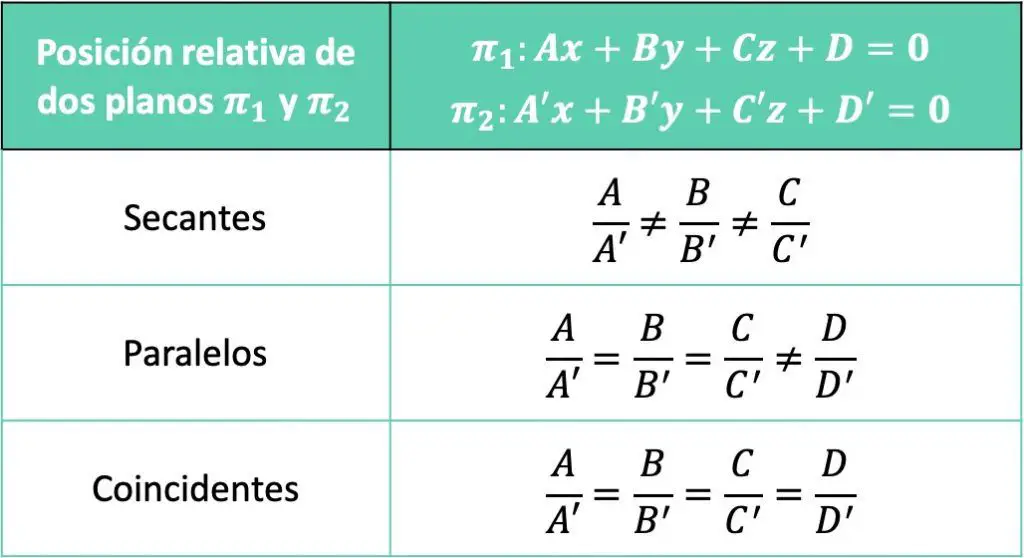
Por tanto, los dos planos serán secantes cuando alguno de los coeficientes A, B o C no sea proporcional con los otros. En cambio, los dos planos serán paralelos cuando únicamente los términos independientes no sean proporcionales. Y, por último, los planos serán coincidentes cuando todos los coeficientes de las dos ecuaciones sean proporcionales.
Distancias en el espacio
A continuación tienes las fórmulas para calcular la distancia que hay entre distintos elementos geométricos: entre un punto y una recta, entre dos planos, entre un plano y una recta,…
Distancia entre dos puntos
La distancia entre dos puntos corresponde al módulo del vector que queda determinado por esos 2 puntos.
De modo que si tenemos dos puntos genéricos:
La fórmula de la distancia entre los dos puntos es:
Distancia de un punto a una recta
La fórmula para calcular la distancia que hay desde un punto hasta una recta en el espacio es la siguiente:
Donde:
es módulo del vector director de la recta
es un punto de la recta
un punto de la recta
y
el vector definido por ambos puntos
es el módulo del producto vectorial entre los vectores
y
Distancia entre dos rectas
La distancia entre dos rectas depende de su posición relativa:
- Si las dos rectas son coincidentes o secantes la distancia entre las dos rectas es igual a cero, ya que se cortan (como mínimo) en un punto.
- Cuando las dos rectas son paralelas o se cruzan debemos aplicar una fórmula según el caso (a continuación dispones de las dos explicaciones).
Distancia entre dos rectas paralelas
Dos rectas paralelas siempre están a la misma distancia entre ellas. De forma que para calcular la distancia entre dos rectas paralelas en el espacio (en R3) se hace de la misma manera que en el plano (en R2): simplemente tenemos que coger un punto de cualquiera de las dos rectas y hallar la distancia que hay desde ese punto hasta la otra recta.
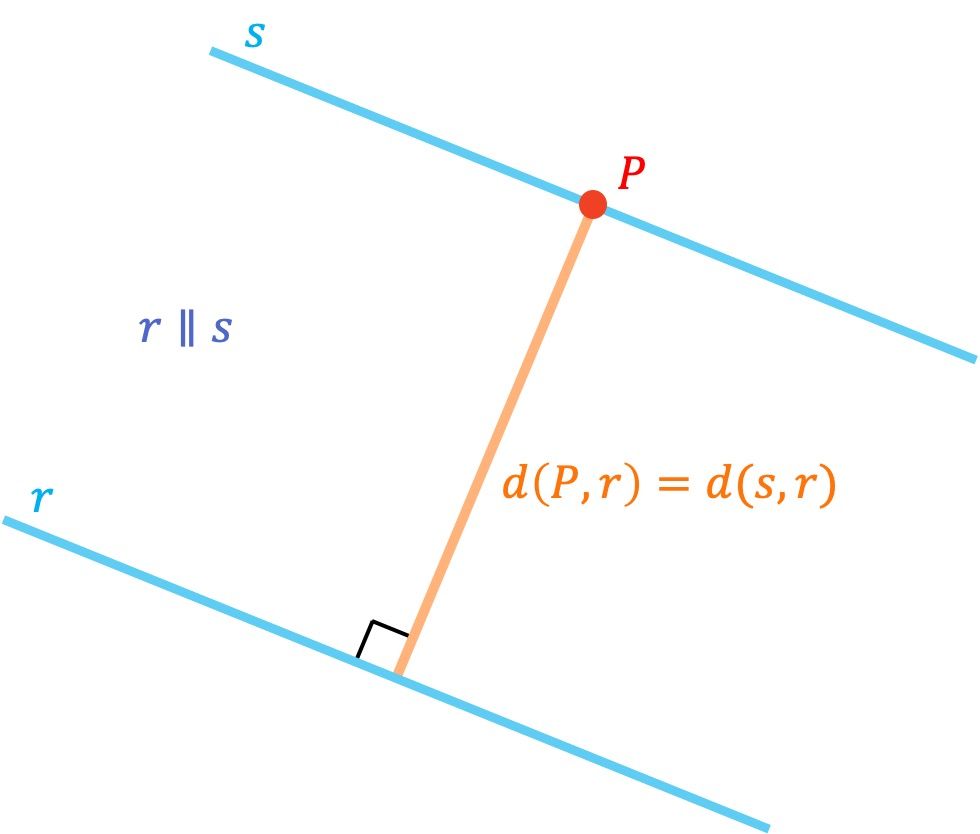
De modo que para determinar la distancia entre 2 rectas paralelas se debe utilizar la fórmula de la distancia entre un punto y una recta.
Distancia entre dos rectas que se cruzan
Sea el vector director y un punto cualquiera de dos rectas que se cruzan:
La fórmula de la distancia entre dos rectas que se cruzan es:
Donde:
es el valor absoluto del producto mixto de los vectores
y el vector definido por los puntos
y
.
es el módulo del producto vectorial entre los vectores directores de las dos rectas cruzadas.
Aunque aquí tienes la fórmula, determinar la distancia entre dos rectas que se cruzan es más complicado de lo que parece. De modo que si quieres practicar en el siguiente enlace podrás ver ejemplos y ejercicios resueltos de la distancia entre dos rectas que se cruzan
Distancia de un punto a un plano
Dados un punto y la ecuación general (o implícita) de un plano:
La fórmula de la distancia de un punto a un plano es:
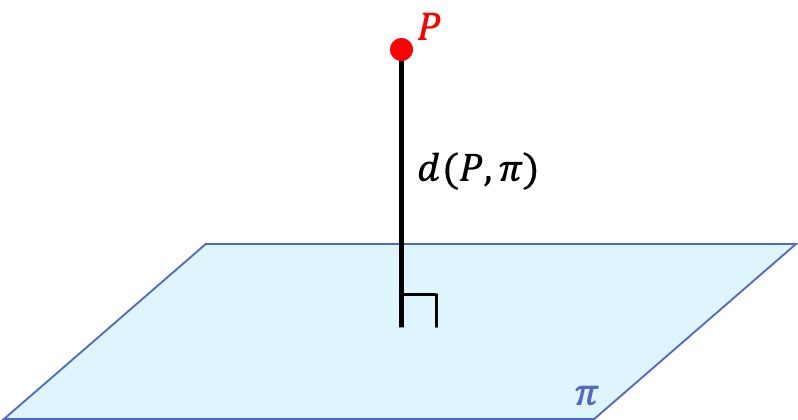
Si al aplicar la fórmula obtenemos un resultado igual a cero, evidentemente significa que la distancia entre el punto y el plano es nula y, por tanto, el punto forma parte de ese plano.
Distancia entre dos planos
La distancia entre dos planos en el espacio depende de la posición relativa entre esos dos planos:
- Si los dos planos son secantes o coincidentes, la distancia entre ellos es igual a cero porque se cortan en algún punto.
- Si los dos planos son paralelos, se calcula la distancia entre los dos planos tomando un punto de cualquiera de los dos planos y calculando la distancia entre dicho punto y el otro plano.
Distancia entre dos planos paralelos
Dos planos paralelos siempre están a la misma distancia entre sí, por lo tanto, para encontrar la distancia entre dos planos paralelos podemos coger un punto de cualquiera de los dos planos y calcular la distancia que hay desde ese punto hasta el otro plano.
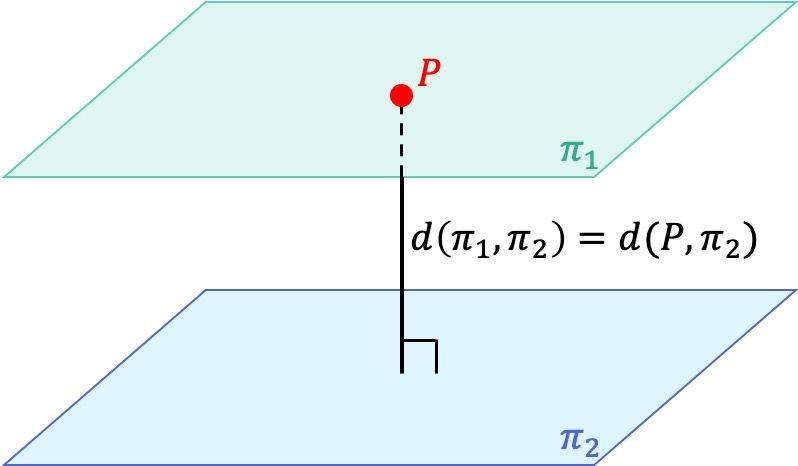
De manera que para calcular la distancia entre dos planos paralelos se debe hallar un punto de uno de los dos planos y luego usar la fórmula de la distancia entre un punto y un plano.
Ángulos en el espacio
Al igual que con las distancias, determinar el ángulo entre dos objetos geométricos en el espacio depende de sus características geométricas. Ya que no es lo mismo calcular el ángulo que forman dos rectas que el que hacen dos planos. Así que a continuación tienes las fórmulas para encontrar los ángulos entre rectas y planos.
Ángulo entre dos rectas
Para averiguar el ángulo entre dos rectas en el espacio euclídeo se debe calcular el ángulo que forman sus vectores directores, por lo tanto:
Dados los vectores directores de dos rectas diferentes:
El ángulo que forman estas dos rectas se puede calcular con la siguiente fórmula:
Donde y
son los módulos de los vectores
y
respectivamente.
Recordemos que la fórmula del módulo de un vector es:
Ángulo entre dos planos
El ángulo entre dos planos es igual al ángulo que forman los vectores normales de dichos planos. Por tanto, para hallar el ángulo entre dos planos se calcula el ángulo que forman sus vectores normales, ya que son equivalentes.
Dada la ecuación general (o implícita) de dos planos distintos:
El vector normal de cada plano es:
Y el ángulo que forman estos dos planos se determina calculando el ángulo que forman sus vectores normales mediante la siguiente fórmula:
Ángulo entre una recta y un plano
El ángulo que forman una recta y un plano se define como el menor de los dos ángulos complementarios que forman el vector director de la recta y el vector normal del plano.
Por lo tanto, si es el vector director de la recta y
es el vector normal al plano:
La fórmula que sirve para calcular el ángulo que forman una recta y un plano es:

En primer lugar, felicitarles por la página web: conceptos muy bien explicados, ejemplos perfectamente descritos y contenidos muy bien organizados.
Soy maestra de primaria y los contenidos me han servido para ayudar a mi sobrino que está cursando 2º de bachillerato; al mismo tiempo me pongo al día en estos contenidos.
Querría saber si sois los mismos que habéis elaborado la web: matricesydeterminantes.com. De ser así, me gustaría saber si tenéis más contenidos de otros temas.
En geometría analítica echo en falta el estudio de la posición de tres planos en el espacio. Por lo demás todo perfecto.
Felicitaros y daros las gracias por vuestro trabajo.
¡Muchísimas gracias Mónica! ❤ ¡Intentamos explicar todo lo mejor posible!
¡Esperamos que os ayude tanto a ti como a tu sobrino! 😉
Sí, también hemos hecho otras páginas web, todas relacionadas con matemáticas:
– matricesydeterminantes.com
– polinomios.org
– ejerciciosecuaciones.com (en proceso de construcción avanzado)
Además, estamos pensando en realizar otras páginas web en un futuro, para explicar otros temas de matemáticas también en detalle.
Por lo que respecta al estudio de la posición relativa de tres planos en el espacio, teníamos pensado ampliar aún más el contenido de esta página, así que la incluimos en la lista de futuros posts. 👍
De nuevo, muchas gracias por tu comentario Mónica, mensajes como este nos motiva a seguir creciendo.