Ecuación continua de la recta

En esta página encontrarás todo sobre la ecuación continua de la recta: qué significa, cómo se calcula a partir de un punto suyo y su vector y cómo se determina con solamente dos puntos. Además, podrás ver varios ejemplos e incluso podrás practicar con ejercicios y problemas resueltos paso a paso.

¿Qué es la ecuación continua de la recta?

Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Así pues, la ecuación continua de la recta es una manera de expresar matemáticamente cualquier recta. Y, para ello, solo es necesario conocer un punto que pertenezca a la recta y el vector director de la recta.

¿Cómo se calcula la ecuación continua de la recta?

Si \vv{\text{v}} es el vector director de la recta y P un punto que pertenece a la recta:

\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)

La fórmula de la ecuación continua de la recta es:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

Donde:

  • x e y son las coordenadas cartesianas de cualquier punto de la recta.
  • P_1 y P_2 son las coordenadas de un punto conocido que forma parte de la recta.
  • \text{v}_1 y \text{v}_2 son las componentes del vector director de la recta.

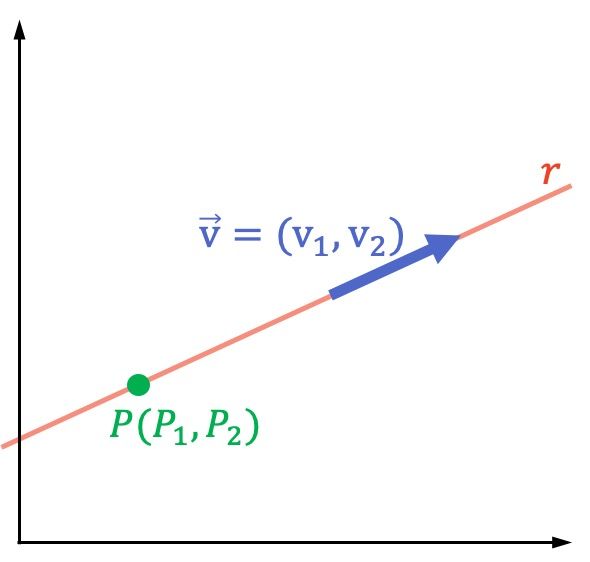
ecuacion continua de la recta 4 definicion

Esta fórmula es para la ecuación continua de la recta en el plano, es decir, cuando trabajamos con puntos y vectores de 2 coordenadas (en R2). Pero si estuviésemos haciendo cálculos en el espacio (en R3) tendríamos que añadir una componente más a la ecuación de la recta:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}

Por otra parte, ten en cuenta que a parte de la ecuación continua existen más formas de expresar analíticamente una recta: la ecuación vectorial, las ecuaciones paramétricas, la ecuación implícita (o general), la ecuación explícita y la ecuación punto-pendiente de una recta. Puedes consultar de qué se trata cada una de ellas en nuestra web.

De hecho, la ecuación continua de una recta se puede conseguir a partir de sus ecuaciones paramétricas. Fíjate en la fórmula de las ecuaciones paramétricas de la recta:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

Si despejamos el parámetro t de cada ecuación paramétrica obtenemos:

t =\cfrac{x-P_1}{\text{v}_1}}

t =\cfrac{y-P_2}{\text{v}_2}}

Igualando las dos ecuaciones resultantes obtenemos la ecuación continua de la recta:

t= t

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

Ejemplo de cómo hallar la ecuación continua de la recta

Veamos cómo se determina la ecuación continua de la recta a partir de un ejemplo:

  • Escribe la ecuación continua de la recta que pasa por el punto P y tiene \vv{\text{v}} como vector director:

\vv{\text{v}}= (4,-2) \qquad P(-1,3)

Para hallar la ecuación continua de la recta, tan solo debemos aplicar su fórmula:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

\cfrac{x-(-1)}{4}=\cfrac{y-3}{-2}

\cfrac{x+1}{4}=\cfrac{y-3}{-2}

Cómo encontrar la ecuación continua de la recta a partir de dos puntos

Un problema habitual de la ecuación continua es que nos dan 2 puntos que pertenecen a la recta y a partir de ellos debemos calcular la ecuación continua. Veamos cómo se resuelve mediante un ejemplo:

  • Halla la ecuación continua de la recta que pasa por los siguientes dos puntos:

A(1,5) \qquad B(3,-4)

Como hemos visto en los apartados de arriba, para calcular la ecuación continua de una recta necesitamos saber su vector director y un punto suyo. Ya tenemos un punto de la recta, pero nos falta su vector director. De modo que primero debemos calcular el vector director de la recta y luego la ecuación continua.

Para determinar el vector director de la recta, basta con calcular el vector que definen los dos puntos dados en el enunciado:

\vv{AB} = B - A = (3,-4) - (1,5) = (2,-9)

Y una vez ya conocemos el vector director de la recta, para hallar la ecuación continua de la recta simplemente debemos aplicar la fórmula:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

\cfrac{x-1}{2}=\cfrac{y-5}{-9}

En este caso hemos cogido el punto A para definir la ecuación continua de la recta, pero también es correcto escribirla con el otro punto que nos dan en el enunciado:

\cfrac{x-3}{2}=\cfrac{y+4}{-9}

Ejercicios resueltos de la ecuación continua de la recta

Ejercicio 1

Halla la ecuación continua de la recta cuyo vector director es \vv{\text{v}} y pasa por el punto P:

\vv{\text{v}}= (5,-4) \qquad P(2,-1)

Para hallar la ecuación continua de la recta simplemente debemos aplicar su fórmula:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

\cfrac{x-2}{5}=\cfrac{y-(-1)}{-4}

\cfrac{x-2}{5}=\cfrac{y+1}{-4}

 

Ejercicio 2

Determina el vector director y un punto de la siguiente recta:

\cfrac{x-1}{6}=\cfrac{y+4}{-5}

La recta del enunciado está expresada en forma de ecuación continua, cuya fórmula es:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

De modo que las componentes del vector director de la recta corresponden a los denominadores de las fracciones:

\vv{\text{v}} = (6,-5)

Y las coordenadas cartesianas de un punto de la recta son los números de los numeradores cambiados de signo:

P(1,-4)

 

Ejercicio 3

Calcula la ecuación continua de la recta que pasa por los siguientes dos puntos:

A(2,-2) \qquad B(8,3)

Para calcular la ecuación continua de una recta necesitamos conocer su vector director y uno de sus puntos. En este caso ya tenemos un punto de la recta, pero nos falta su vector director. De manera que primero debemos calcular el vector director de la recta y luego la ecuación continua.

Para encontrar el vector director de la recta, basta con calcular el vector que definen los dos puntos dados en el enunciado:

\vv{AB} = B - A = (8,3) - (2,-2) = (6,5)

Y una vez ya sabemos el vector director de la recta, para hallar su ecuación continua simplemente aplicamos la fórmula:

\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}

\cfrac{x-2}{6}=\cfrac{y+2}{5}

En este caso hemos escogido el punto A para definir la ecuación continua, pero también es válido escribirla con el otro punto que nos dan en el enunciado:

\cfrac{x-8}{6}=\cfrac{y-3}{5}

 

Ejercicio 4

Dado el siguiente punto:

P(0,3)

Determina si pertenece o no a la recta definida por la siguiente ecuación continua:

\cfrac{x+2}{2}=\cfrac{y-3}{-4}

Para comprobar si el punto pertenece a la recta, tenemos que sustituir las coordenadas del punto en la ecuación de la recta. Si el punto satisface la ecuación significará que efectivamente pertenece a la recta, en cambio, si la ecuación no se cumple implicará que el punto no forma parte de la recta.

Por lo tanto, sustituimos las coordenadas del punto en la ecuación de la recta dada:

\cfrac{0+2}{2}=\cfrac{3-3}{-4}

Y operamos:

\cfrac{2}{2}=\cfrac{0}{-4}

1 \neq 0

1 no es igual a 0, por lo que el punto no cumple la ecuación de la recta y, en consecuencia, no pertenece a la recta.

 

Ejercicio 5

Encuentra la ecuación continua de la recta a partir de sus ecuaciones paramétricas:

\displaystyle \begin{cases} x=-2+4t\\[1.7ex] y=-3t \end{cases}

Para pasar de las ecuaciones paramétricas a la ecuación continua de la recta, debemos despejar el parámetro t de cada ecuación paramétrica:

t =\cfrac{x+2}{4}

t =\cfrac{y}{-3}

Y luego igualamos las dos ecuaciones resultantes y de esta manera obtenemos la ecuación continua de la recta:

t= t

\cfrac{x+2}{4}=\cfrac{y}{-3}

 

4 comentarios en “Ecuación continua de la recta”

    1. Geometría Analítica

      Hola Juan Diego, si trabajamos en 3 dimensiones tenemos que añadir la coordenada z, por tanto, la ecuación continua en un espacio tridimensional es:
      \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}

      Entonces, para resolver el problema que propones primero debemos calcular el vector de la recta:
      \vv{\text{v}}=P-Q=(5,6,7)-(8,5,6)=(-3,1,1)

      Y luego sustituimos las coordenadas del vector y de un punto de la recta en la fórmula de la ecuación continua:
      \cfrac{x-5}{-3}=\cfrac{y-6}{1}= \cfrac{z-7}{1}

      Nota: en este caso los tres puntos que proponías no forman parte de la misma recta, ya que los vectores entre ellos no son proporcionales. Te he resuelto el ejercicio como si los 3 puntos fueran de la misma recta para que veas cómo se calcula la ecuación continua de la recta en este caso.

    1. Geometría Analítica

      Hola Monick,

      Necesitas saber un punto que pertenezca a la recta para averiguar el parámetro a.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio