Ecuación canónica, segmentaria o simétrica de la recta

Aquí encontrarás la explicación de cuál es la fórmula de la ecuación canónica (o segmentaria) de la recta, también llamada ecuación simétrica. Además, podrás ver ejemplos y practicar con ejercicios resueltos. E, incluso, hallarás cómo se calcula la ecuación canónica a partir de la ecuación general (o implícita) de la recta.

¿Qué es la ecuación canónica o segmentaria de la recta?

Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Así pues, la ecuación canónica de la recta, también llamada ecuación segmentaria de la recta, es una forma de expresar matemáticamente cualquier recta. Para ello, solo es necesario conocer los puntos de corte con los ejes de coordenadas de dicha recta.

Por otro lado, en geometría analítica la ecuación canónica (o segmentaria) de la recta también se denomina ecuación simétrica de la recta.

Fórmula de la ecuación canónica o segmentaria de la recta

La ecuación canónica o segmentaria de la recta es la expresión algebraica de la recta que se puede determinar conociendo los valores dónde la recta interseca al eje de las abscisas y al eje de las ordenadas.

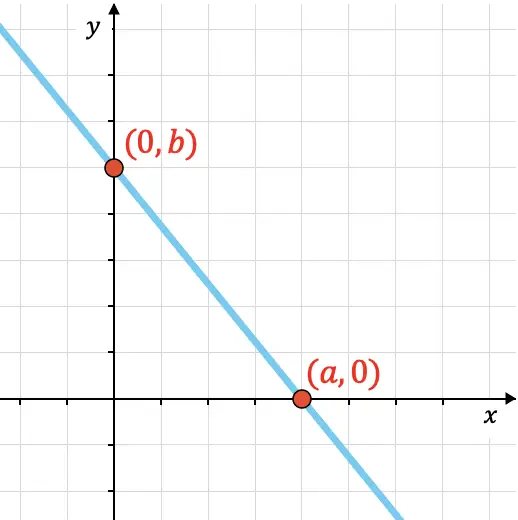
Hay que destacar que no existe la ecuación canónica (o segmentaria) de la recta en ninguno de los siguientes tres casos:

1. Cuando la recta es vertical, es decir, paralela al eje OY. Porque la ecuación de una recta vertical es
2. Cuando la recta es horizontal, esto es, paralela al eje OX. Porque la ecuación de una recta horizontal es
3. Cuando la recta pasa por el origen de coordenadas (punto ), ya que entonces tendríamos dos indeterminaciones en la ecuación de la recta.

Ejemplo de cómo hallar la ecuación canónica o segmentaria de la recta

Para que puedas entender mejor el concepto, vamos a resolver un problema de la ecuación segmentaria (o canónica) de la recta:

• Halla la ecuación canónica o segmentaria de la recta que pasa por los siguientes dos puntos:

En este caso, el enunciado no nos está dando 2 puntos cualesquiera, sino que se trata de los dos puntos de corte con los ejes.

Punto de corte de la recta con el eje X:

Punto de corte de la recta con el eje Y:

Por lo tanto, como ya sabemos los dos puntos de intersección con los ejes, simplemente debemos aplicar la fórmula de la ecuación canónica o segmentaria de la recta:

Y, finalmente, sustituimos el valor de los parámetros y en la fórmula:

Ahora ya conoces cuál es la ecuación canónica (o segmentaria) de la recta. Sin embargo, debes saber que existen más formas de expresar una recta, y entre ellas destaca la ecuación explícita. Este tipo de ecuación de la recta resulta difícil de entender bien del todo, por lo que te hemos explicado todo sore ella detalladamente en la página del enlace.

Calcular la ecuación canónica o segmentaria de la recta a partir de su ecuación general

Acabamos de ver una forma de determinar la ecuación canónica o segmentaria de la recta, pero también existen otros métodos:

La ecuación canónica o segmentaria de una recta se puede obtener a partir de la ecuación general (o implícita) de la misma recta:

En primer lugar, cambiamos de lado al coeficiente C:

Luego dividimos toda la ecuación por el valor del parámetro C cambiado de signo:

Y, mediante las propiedades de las fracciones, llegamos a la fórmula de la ecuación canónica o segmentaria de la recta:

Por lo tanto, de esta fórmula se deduce que los términos y de la ecuación canónica de una recta son equivalentes a las siguientes expresiones:

Ejercicios resueltos de la ecuación canónica o segmentaria de la recta

Ejercicio 1

¿Cuáles son los puntos de corte con los ejes coordenados de la siguiente recta?

La recta del ejercicio está expresada en forma de ecuación canónica o segmentaria de la recta, cuya fórmula es:

Por lo tanto, los puntos donde la recta interseca con los ejes de coordenadas son:

Punto de corte con el eje X:

Punto de corte con el eje Y:

 

Ejercicio 2

¿Cuál es la ecuación canónica o segmentaria de la recta que está representada gráficamente?

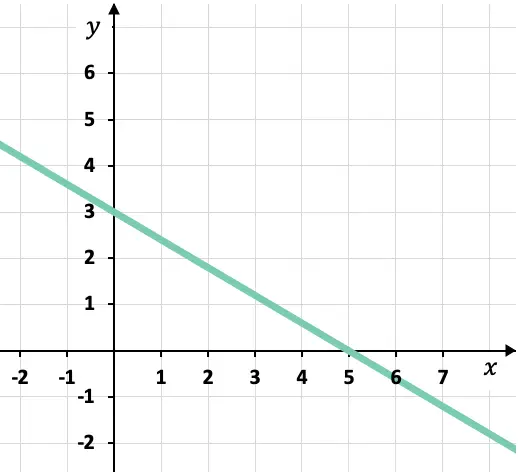
A partir del gráfico podemos saber los puntos donde la recta cruza los ejes de coordenadas:

Punto de corte de la recta con el eje X:

Punto de corte de la recta con el eje Y:

Por lo tanto, una vez ya sabemos los 2 puntos de intersección con los ejes, simplemente debemos utilizar la fórmula de la ecuación canónica o segmentaria de la recta:

Y, por último, sustituimos el valor de los parámetros y en la fórmula:

 

Ejercicio 3

Calcula la ecuación canónica o segmentaria de la recta que queda determinada por la siguiente ecuación general (o implícita):

Para pasar de ecuación general a ecuación segmentaria, primero tenemos que despejar el término independiente de la ecuación:

En segundo lugar, dividimos toda la ecuación por el coeficiente del miembro derecho de la ecuación:

La expresión anterior es equivalente a la siguiente:

De modo que la ecuación canónica, segmentaria o simétrica de la recta es:

 

Ejercicio 4

Determina la ecuación canónica o segmentaria cuyo vector director es y pasa por el punto

Primero encontramos fácilmente la ecuación continua de la recta a partir de su vector director y un punto que pertenece a la recta:

Ahora calculamos la ecuación general de la recta multiplicando las fracciones en cruz y agrupando los términos resultantes:

Por lo que solo nos queda convertir la ecuación general de la recta a ecuación canónica. Para ello, primero despejamos el término independiente de la ecuación:

Después dividimos toda la ecuación por el coeficiente del miembro derecho de la ecuación:

La expresión anterior es equivalente a la siguiente:

Negativo entre negativo es igual a positivo:

Las fracciones no se pueden simplificar más, por lo tanto, la ecuación canónica, segmentaria o simétrica de la recta es: