Distancia entre dos rectas que se cruzan (fórmula)

En esta página encontrarás cómo determinar la distancia entre dos rectas que se cruzan (fórmula). Además, podrás ver ejemplos y practicar con ejercicios resueltos de distancias entre rectas que se cruzan.

¿Qué son dos rectas que se cruzan?

Antes de ver cómo se calcula la distancia entre dos rectas que se cruzan, repasemos muy brevemente exactamente en qué consiste esta tipo de posición relativa entre dos rectas:

Dos rectas que se cruzan, también llamadas rectas cruzadas, son dos rectas distintas que tienen una dirección diferente y no se cortan en ningún punto. Por lo tanto, dos rectas cruzadas no están en el mismo plano.

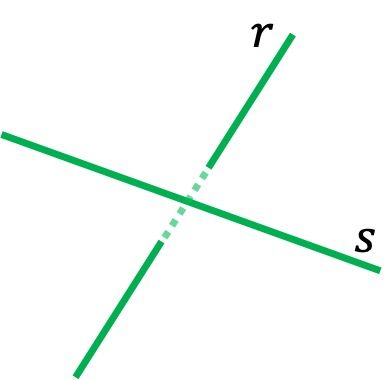
distancia entre dos rectas que se cruzan 2 bachillerato

Por ejemplo, en la representación gráfica de arriba la recta s siempre está delante de la recta r, por lo que nunca se tocarán entre sí.

Cómo calcular la distancia entre dos rectas que se cruzan

Existen varios métodos para determinar la distancia que hay entre dos rectas que se cruzan en el espacio. En esta página solo te explicaremos un procedimiento, el más fácil, porque los otros dos métodos son más largos y complicados, de hecho, casi ni se utilizan.

Sea el vector director y un punto cualquiera de dos rectas que se cruzan:

\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}

La fórmula de la distancia entre dos rectas que se cruzan es:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Donde \left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| es el valor absoluto del producto mixto de los vectores \vv{\text{u}}, \vv{\text{v}} y el vector definido por los puntos A y B. Y, por otra parte, \lvert \vv{\text{u}} \times \vv{\text{v}} \rvert es el módulo del producto vectorial de los vectores directores de las dos rectas cruzadas.

Por lo tanto, para poder encontrar la distancia que hay entre 2 rectas que se cruzan debes saber cómo calcular el triple producto escalar (o producto mixto de tres vectores) y el producto cruz (o producto vectorial de dos vectores). Puedes repasar cómo se hacía en los enlaces anteriores, donde encontrarás las fórmulas correspondientes, ejemplos y ejercicios resueltos.

Ejemplo de cómo hallar la distancia entre dos rectas que se cruzan

Para que puedas ver cómo determinar la distancia entre dos rectas cruzadas, vamos a resolver un problema a modo de ejemplo:

  • ¿Cuál es la distancia entre las siguientes dos rectas que se cruzan?

r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}

s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}

En primer lugar, tenemos que identificar el vector director y un punto de cada recta. Ambas rectas están expresadas en forma de ecuación continua, por tanto:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}

Y ahora aplicamos la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Por un lado resolvemos el producto mixto:

\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13

Y, por otra parte, hallamos el módulo del producto vectorial:

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}

Finalmente, sustituimos el valor de cada término en la fórmula de la distancia entre dos rectas cruzadas:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}

Ejercicios resueltos de distancias entre dos rectas que se cruzan

Ejercicio 1

Halla la distancia entre las siguientes dos rectas que se cruzan en un punto:

r: \ \cfrac{x-1}{2} = \cfrac{y+1}{1} = \cfrac{z+3}{2}

s: \ \cfrac{x-2}{3} = \cfrac{y-4}{-1} = \cfrac{z-1}{2}

En primer lugar, tenemos que averiguar el vector director y un punto de cada recta. Las dos rectas están definidas en forma de ecuación continua, por lo tanto:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,1,2) \\[2ex] A(1,-1,-3) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(3,-1,2) \\[2ex] B(2,4,1)\end{cases}

Y ahora utilizamos la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Determinamos el producto mixto:

\vv{AB} = B - A = (2,4,1) - (1,-1,-3) = (1,5,4)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&1&2 \\[1.1ex] 3&-1&2 \\[1.1ex] 1&5&4 \end{vmatrix}\right| = \left| -6 \right| =6

Luego calculamos el módulo del producto vectorial:

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&1&2 \\[1.1ex] 3&-1&2 \end{vmatrix}=4\vv{i} +2\vv{j}-5\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{4^2+2^2+(-5)^2} = \sqrt{16+4+25} = \sqrt{45}

Y, por último, sustituimos el valor de cada término en la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{6}{\sqrt{45}}= \bm{0,89}

 

Ejercicio 2

Calcula la distancia entre las siguientes dos rectas que se cruzan:

r: \ \cfrac{x-2}{3} = \cfrac{y-4}{1} = \cfrac{z+2}{-1}

s: \ \cfrac{x+1}{2} = \cfrac{y+2}{-2} = \cfrac{z-1}{5}

En primer lugar, tenemos que identificar el vector director y un punto de cada recta. Las dos rectas están expresadas en forma de ecuación continua, por tanto:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(3,1,-1) \\[2ex] A(2,4,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(2,-2,5) \\[2ex] B(-1,-2,1)\end{cases}

Y ahora usamos la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Determinamos el producto mixto:

\vv{AB} = B - A = (-1,-2,1) - (2,4.-2) = (-3,-6,3)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 3&1&-1 \\[1.1ex] 2&-2&5 \\[1.1ex] -3&-6&3 \end{vmatrix}\right| = \left| 69 \right| =69

Luego calculamos el módulo del producto vectorial:

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3&1&-1 \\[1.1ex] 2&-2&5 \end{vmatrix}=3\vv{i} -17\vv{j}-8\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{3^2+(-17)^2+(-8)^2} = \sqrt{9+289+64} = \sqrt{362}

Y, por último, sustituimos el valor de cada incógnita en la fórmula de la distancia entre dos rectas cruzadas:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{69}{\sqrt{362}}= \bm{3,63}

 

Ejercicio 3

Encuentra la distancia entre las siguientes dos rectas que se cruzan:

\displaystyle r: \ \begin{cases} x= -4t \\[1.7ex] y=2+3t \\[1.7ex] z=-1+t \end{cases}

\displaystyle s: \ (x,y,z)=(4,2,1)+t(3,2,-5)

En primer lugar, tenemos que hallar el vector director y un punto de cada recta. La recta r está en forma de ecuaciones paramétricas y la recta s en forma de ecuación vectorial, por lo tanto:

\displaystyle r: \ \begin{cases} \vv{\text{u}} =(-4,3,1) \\[2ex] A(0,2,-1) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(3,2,-5) \\[2ex] B(4,2,1)\end{cases}

Y ahora empleamos la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}

Determinamos el triple producto escalar:

\vv{AB} = B - A = (4,2,-1) - (0,2,1) = (4,0,-2)

\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} -4&3&1 \\[1.1ex] 3&2&-5 \\[1.1ex] 4&0&-2 \end{vmatrix}\right| = \left| -34 \right| =34

Luego calculamos el módulo del producto cruz:

\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -4&3&1 \\[1.1ex] 3&2&-5 \end{vmatrix}=-17\vv{i} -17\vv{j}-17\vv{k}

\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{(-17)^2+(-17)^2+(-17)^2} = \sqrt{289+289+289} = \sqrt{867}

Y, por último, sustituimos el valor de cada término en la fórmula de la distancia entre dos rectas que se cruzan:

d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{34}{\sqrt{867}}= \bm{1,15}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio