En esta página encontrarás todo sobre la ecuación explícita de la recta: qué es, cuál es su fórmula, ejemplos de cómo se calcula,… También hallarás una explicación detallada de qué significan la pendiente y la ordenada en el origen de la ecuación explicita. Y, además, verás diferentes ejemplos y podrás practicar con ejercicios resueltos paso a paso.
Índice
¿Qué es la ecuación explícita de la recta?
Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.
Así pues, la ecuación explícita de la recta es una forma de expresar matemáticamente cualquier recta. Para ello, solo es necesario conocer la pendiente de la recta y el punto en el que corta el eje Y.
Fórmula de la ecuación explícita de la recta
La fórmula de la ecuación explícita de la recta es:
Donde es la pendiente de la recta y
su ordenada en el origen, es decir, la altura a la que corta el eje Y.
Veamos cómo se calcula la ecuación explícita de la recta mediante un ejemplo:
- Escribe la ecuación explícita de la recta que pasa por el punto
y tiene como pendiente m=2.
La fórmula de la ecuación explícita de la recta es:
En este caso el enunciado nos dice que la pendiente de la recta es m=2, por tanto, la ecuación de la recta será de la siguiente forma:
De manera que solo nos falta calcular el coeficiente n. Para ello, debemos sustituir un punto que pertenezca a la recta en su ecuación. Y en este caso el enunciado nos dice que la recta pasa por el punto por tanto:
Y resolvemos la ecuación resultante para hallar el valor de n:
Por lo tanto, la ecuación explícita de la recta es:
Ten en cuenta que, a parte de la ecuación explícita, hay más maneras de expresar analíticamente una recta. Como por ejemplo la ecuación vectorial, que es un tipo de ecuación de la recta diferente a todas las otras porque se expresan el vector director y un punto de la recta con sus propias coordenadas. En el enlace podrás ver en qué consiste y por qué es tan peculiar.
Significado de los parámetros m y n
Como hemos visto en la definición de ecuación explícita de la recta, el parámetro es la pendiente de la recta y
su ordenada en el origen. Pero… ¿qué significa esto? Veámoslo a partir de la representación gráfica de una recta:
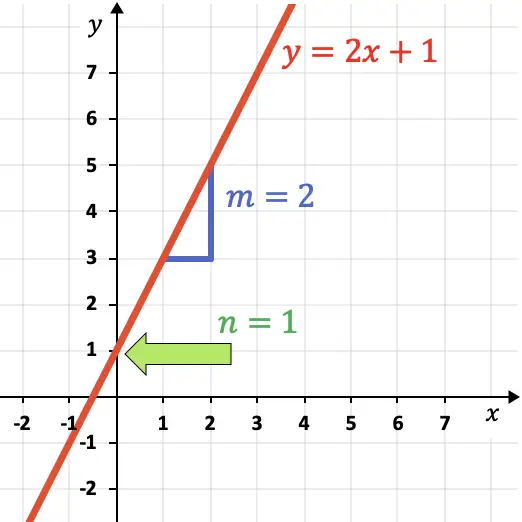
El término independiente es el punto de corte de la recta con el eje de las ordenadas (eje OY). En el gráfico de arriba
es igual a 1 porque la recta interseca con el eje Y en y=1.
Por otro lado, el término indica la pendiente de la recta, es decir, su inclinación. Como ves en la gráfica,
es igual a 2 ya que la recta sube 2 unidades verticales por cada 1 unidad horizontal.
Evidentemente, si la pendiente es positiva la función es creciente (va hacia arriba), en cambio, si la pendiente es negativa la función es decreciente (va hacia abajo).
Calcular la pendiente de una recta
A parte, existen 3 maneras distintas para determinar numéricamente la pendiente de una recta:
- Dados dos puntos diferentes de la recta
y
la pendiente de la recta es igual a:
- Si
es el vector director de la recta, su pendiente es:
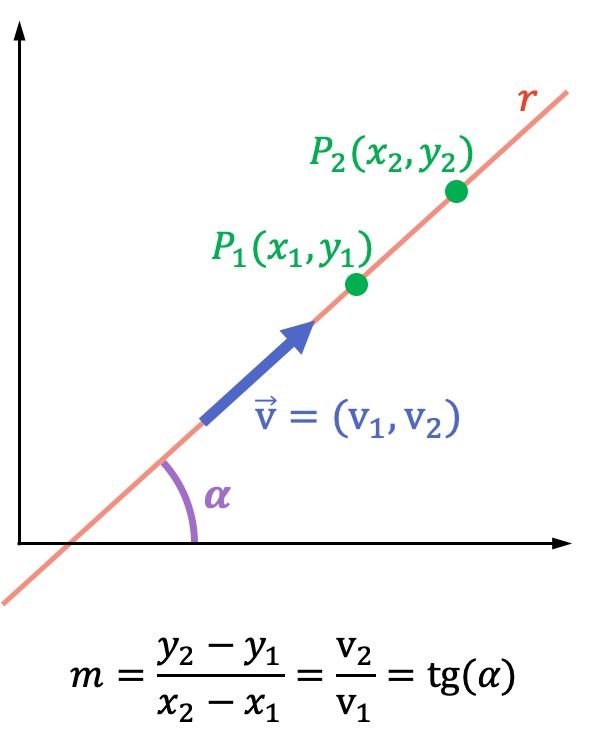
- Si
es el ángulo que forma la recta con el eje de las abscisas (eje X), la pendiente de la recta es equivalente a la tangente de dicho ángulo:
Posición relativa de las rectas
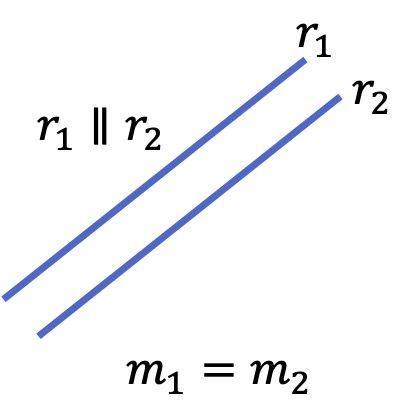
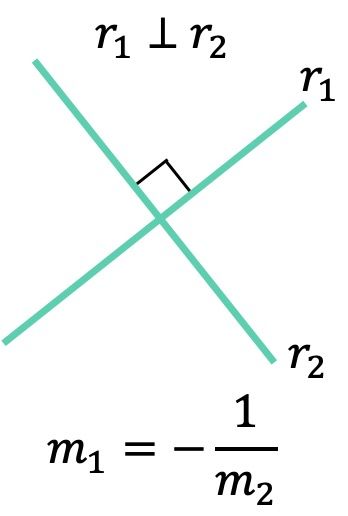
Finalmente, la pendiente de una recta también sirve para saber la relación que hay entre varias rectas. Ya que dos rectas paralelas tienen la misma pendiente y, por contra, si la pendiente de una recta es la inversa negativa de la pendiente de otra recta significa que esas dos rectas son perpendiculares.
Calcular la ecuación explícita de la recta que pasa por dos puntos
Un problema muy típico es encontrar la ecuación explícita de una recta a partir de dos puntos por los que pasa. Veamos cómo se resuelve a través de un ejemplo:
- Determina la ecuación explícita de la recta que pasa por los siguientes dos puntos:
Para hallar la ecuación explícita de la recta tenemos que averiguar cuánto valen los parámetros m y n. Así que primero calculamos la pendiente de la recta mediante la fórmula de los dos puntos:
Y luego podemos hallar la ordenada en el origen sustituyendo un punto de la recta en la ecuación:
De modo que la ecuación explícita de la recta es:
Hallar la ecuación explícita a partir de la ecuación implícita
Finalmente, otro tipo de problema con el que nos encontramos a menudo es encontrar la ecuación explícita de la recta partiendo de su ecuación implícita (también conocida como ecuación general o cartesiana). Evidentemente, para entender el siguiente método debes conocer perfectamente qué es y cómo es la ecuación implícita; pero si no lo recuerdas del todo puedes consultarlo en el enlace.
Entonces, si ya dominas la ecuación implícita (o general) de una recta, veamos cómo es este procedimiento:
- Encuentra la ecuación explícita de la siguiente recta:
Lo único que debemos hacer para averiguar la ecuación explícita de la recta es despejar la variable Así que pasamos los términos sin
al otro lado de la ecuación:
Ahora despejamos la variable
Y, por último, simplificamos:
Por lo tanto, la pendiente de esta recta es y su ordenada en la origen es 4.
Ejercicios resueltos de ecuación explícita
Ejercicio 1
Indica la pendiente y la ordenada en el origen de las siguientes rectas:
La ecuación explícita de una recta sigue la siguiente fórmula:
Donde es la pendiente y
la ordenada en el origen. Por tanto:
La última recta está expresada mediante su ecuación implícita, por lo que primero debemos pasarla a ecuación explícita (despejando ) y luego ya podremos identificar los parámetros:
Ejercicio 2
Calcula la ecuación explícita de la recta que pasa por el punto y tiene como pendiente
La fórmula de la ecuación explícita de la recta es:
En este caso la pendiente de la recta debe ser -2, por tanto, la ecuación de la recta tendrá la siguiente forma:
De manera que solo nos falta calcular el coeficiente n. Para ello, debemos sustituir un punto que pertenezca a la recta en su ecuación y resolver la ecuación resultante:
En definitiva, la ecuación explícita de la recta es:
Ejercicio 3
Halla la ecuación explícita de la recta que pasa por los siguientes dos puntos:
Para hallar la ecuación explícita de la recta tenemos que averiguar cuánto valen los parámetros m y n. Así que primero calculamos la pendiente de la recta a partir de las coordenadas de los dos puntos:
Y luego determinamos la ordenada en el origen sustituyendo un punto de la recta en la ecuación:
De modo que la ecuación explícita de la recta es:
Ejercicio 4
Calcula la ecuación explícita de la recta que forma un ángulo de 45º con el eje X y pasa por el origen de coordenadas.
Si la recta forma un ángulo de 45 grados con el eje OX, su pendiente será:
Y una vez sabemos la pendiente de la recta, podemos calcular la ordenada en el origen sustituyendo un punto de la recta en la ecuación. Además, el enunciado nos dice que la recta pasa por el origen de coordenadas, lo que significa que pasa por el punto (0,0). Por tanto:
De modo que la ecuación explícita de la recta es:
Ejercicio 5
Encuentra la ecuación explícita de la recta paralela a la recta y que pasa por el punto
Siendo la recta
Para que la recta sea paralela a la recta ambas deben tener la misma pendiente, por lo tanto:
Y una vez sabemos la pendiente de la recta, podemos calcular la ordenada en el origen sustituyendo el punto que pertenece a la recta en la ecuación:
Por lo que la ecuación explícita de la recta es:
Ejercicio 6
¿Cuál es la ecuación explícita de cada recta que está representada gráficamente?
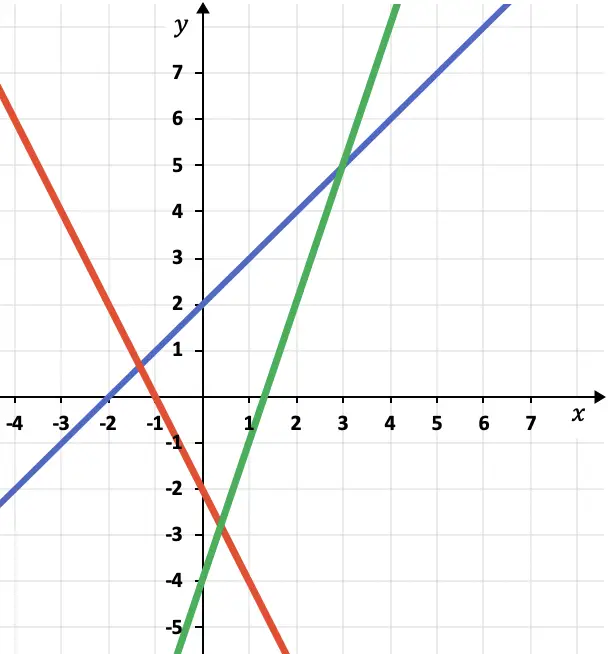
Recta azul
La recta azul aumenta una Y por cada X, por lo tanto, su pendiente es igual a 1. Por otro lado, la recta corta con el eje Y en el 2, así que su ordenada en el origen es 2.
Recta verde
La recta verde aumenta tres Y por cada X, por lo que su pendiente es 3. Además, la recta interseca con el eje Y en el -4, de modo que que su ordenada en el origen es -4.
Recta roja
La recta roja disminuye dos Y por cada X, por lo tanto, su pendiente es equivalente a -2. Y la recta corta con el eje de las ordenadas en y=-2, de forma que su ordenada en el origen también es -2.

Son muy buenos ejemplos de aplicación. Gracias y felicitaciones
Muy útil y explicado de manera clara y sencilla. Muchas gracias.