Ecuación vectorial de la recta

En esta página encontrarás cómo calcular la ecuación vectorial de la recta. Además, podrás ver varios ejemplos y practicar con ejercicios resueltos. Y también hallarás cómo se obtienen puntos de una recta a partir de su ecuación vectorial.

¿Qué es la ecuación vectorial de la recta?

Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Así pues, la ecuación vectorial de la recta es una manera de expresar matemáticamente cualquier recta. Y, para ello, solo es necesario un punto que pertenezca a la recta y el vector director de la recta.

¿Cómo se calcula la ecuación vectorial de la recta?

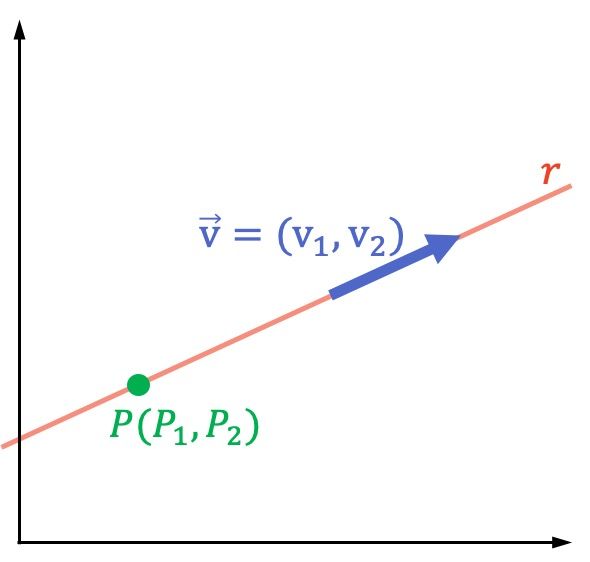
Si \vv{\text{v}} es el vector director de la recta y P un punto que pertenece a la recta:

\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P_1,P_2)

La fórmula de la ecuación vectorial de la recta es:

(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)

Donde:

  • x e y son las coordenadas cartesianas de cualquier punto de la recta.
  • P_1 y P_2 son las coordenadas de un punto conocido que forma parte de la recta.
  • \text{v}_1 y \text{v}_2 son las componentes del vector director de la recta.
  • t es un escalar (un número real) cuyo valor depende de cada punto de la recta.

ecuacion vectorial de la recta 4 eso

Esta es la ecuación vectorial de la recta en el plano, es decir, cuando trabajamos con puntos y vectores de 2 coordenadas (en R2). Sin embargo, si estuviésemos haciendo cálculos en el espacio (en R3) tendríamos que añadir una componente más a la ecuación de la recta:

(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)

Por otro lado, ten en cuenta que, a parte de la ecuación vectorial, existen más formas de expresar analíticamente una recta: las ecuaciones paramétricas, la ecuación continua, la ecuación implícita (o general), la ecuación explícita y la ecuación punto-pendiente de una recta. Puedes ver todos los tipos de ecuaciones de la recta en este enlace.

Ejemplo de cómo hallar la ecuación vectorial de la recta

Veamos cómo se determina la ecuación vectorial de la recta a partir de un ejemplo:

  • Escribe la ecuación vectorial de la recta que pasa por el punto P y tiene \vv{\text{v}} como vector director:

\vv{\text{v}}= (1,2) \qquad P(3,0)

Para hallar la ecuación vectorial de la recta, tan solo tenemos que aplicar su fórmula:

(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)

(x,y)=(3,0)+t\cdot (1,2)

Obtener puntos a partir de la ecuación vectorial de la recta

Una vez hemos hallado la ecuación vectorial de la recta, es muy fácil calcular puntos por los que pase la recta. Para determinar un punto de una recta tan solo debemos otorgar un valor al parámetro \bm{t} de la ecuación vectorial de la recta.

Por ejemplo, dada la siguiente ecuación vectorial de la recta:

(x,y)=(1,-1)+t\cdot (2,3)

Se consigue un punto sustituyendo t por un número cualquiera, por ejemplo t=1:

\begin{aligned}(x,y)& =(1,-1)+1\cdot (2,3)\\[2ex] & =(1,-1)+(2,3) \\[2ex] & = (1+2 \ , -1+3) \\[2ex] & = \bm{(3,2)} \end{aligned}

Y podemos calcular otro punto de la recta dando a la incógnita t un número diferente, por ejemplo t=2:

\begin{aligned}(x,y)& =(1,-1)+2\cdot (2,3)\\[2ex] & =(1,-1)+(4,6) \\[2ex] & = (1+4 \ , -1+6) \\[2ex] & = \bm{(5,5)} \end{aligned}

Por lo tanto, podemos conseguir infinitos puntos de la recta, porque la variable t puede tomar infinitos valores.

Ejercicios resueltos de la ecuación vectorial de la recta

Ejercicio 1

Encuentra la ecuación vectorial de la recta que pasa por el punto P y cuyo vector director es \vv{\text{v}}:

P(-1,3) \qquad \vv{\text{v}}=(4,-2)

Para calcular la ecuación vectorial de la recta simplemente debemos aplicar su fórmula:

(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)

(x,y)=(-1,3)+t\cdot (4,-2)

 

Ejercicio 2

Calcula tres puntos que sean de la recta del problema anterior.

Para conseguir puntos de una recta descrita con la ecuación vectorial, se debe otorgar valores al parámetro t. La ecuación vectorial calculada en el problema anterior es:

(x,y)=(-1,3)+t\cdot (4,-2)

Para calcular un punto sustituimos la incógnita t por ejemplo por t=1:

\begin{aligned}(x,y)& =(-1,3)+1\cdot (4,-2)\\[2ex] & =(-1,3)+ (4,-2) \\[2ex] & = (-1+4 \ , 3-2) \\[2ex] & = \bm{(3,1)} \end{aligned}

Para hallar un segundo punto damos a t por ejemplo el valor de t=2:

\begin{aligned}(x,y)& =(-1,3)+2\cdot (4,-2)\\[2ex] & =(-1,3)+ (8,-4) \\[2ex] & = (-1+8 \ , 3-4) \\[2ex] & = \bm{(7,-1)} \end{aligned}

Y, finalmente, obtenemos el tercer punto otorgando a t el valor de t=3:

\begin{aligned}(x,y)& =(-1,3)+3\cdot (4,-2)\\[2ex] & =(-1,3)+ (12,-6) \\[2ex] & = (-1+12 \ , 3-6) \\[2ex] & = \bm{(11,-3)} \end{aligned}

Puede que hayas obtenido distintos puntos, ya que esto depende de los valores que le des al parámetro t. Pero si has seguido el mismo procedimiento está bien.

 

Ejercicio 3

Dados dos puntos:

A(5,1) \qquad B(3,-2)

Calcula la ecuación vectorial de la recta que pasa por esos dos puntos.

En este caso no tenemos el vector director de la recta, por lo que primero debemos encontrar su vector director y luego la ecuación de la recta.

De manera que para hallar el vector director de la recta tenemos que calcular el vector definido por los dos puntos dados:

\vv{AB}=B-A= (3,-2)- (5,1) = (-2,-3)

Y una vez ya sabemos el vector director de la recta, podemos determinar su ecuación vectorial a partir de uno de los puntos dados y de la fórmula:

(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)

(x,y)=(5,1)+t\cdot (-2,-3)

También es válida la ecuación que se encuentra poniendo el otro punto dado en la fórmula:

(x,y)=(3,-2)+t\cdot (-2,-3)

 

2 comentarios en “Ecuación vectorial de la recta”

  1. Nelson Barrezueta

    Hola, muy agradecido me ha sido de mucha ayuda
    Pero, me quedó una duda el primer ejercicio propuesto me parece que hay un pequeño error o será que yo me confundí.

    Responder
    1. Geometría Analítica

      Hola Nelson,

      Tenías razón, había un fallo en el primer ejercicio porque el punto y el vector estaban puestos al revés, ya se ha corregido. ¡Muchas gracias por avisar! 🙂

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio