▷ Hallar la ecuación Implícita o General (o Cartesiana) de la recta

En esta página encontrarás cómo se calcula la ecuación implícita de la recta, también llamada ecuación general o cartesiana de la recta. Además, podrás ver varios ejemplos e incluso podrás practicar con ejercicios resueltos paso a paso de rectas.

Índice

¿Qué es la ecuación implícita, general o cartesiana de la recta?

Recordemos que la definición matemática de una recta es un conjunto de puntos consecutivos que están representados en la misma dirección sin curvas ni ángulos.

Así pues, la ecuación implícita de la recta, también conocida como ecuación general o cartesiana, es una manera de expresar matemáticamente cualquier recta. Para ello, solo es necesario el vector director de la recta y un punto que pertenezca a la recta.

Fórmula de la ecuación implícita, general o cartesiana de la recta

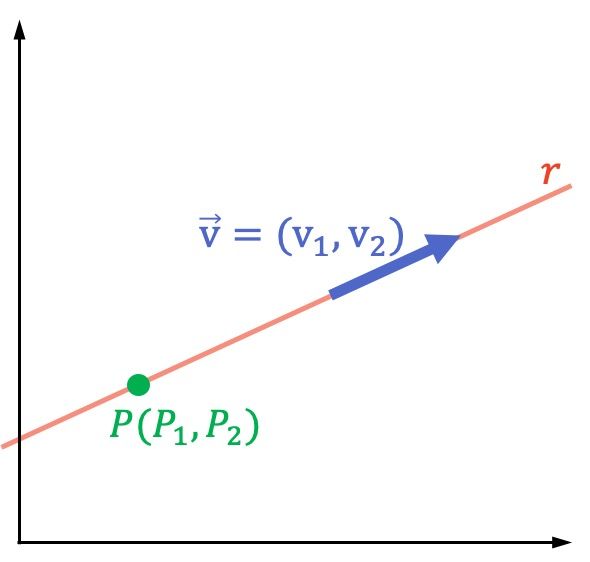
Si $\vv{\text{v}}$ es el vector director de la recta y $P$ un punto que pertenece a la recta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

La fórmula de la ecuación implícita, general o cartesiana de la recta es:

$Ax+By+C=0$

Donde:

$x$ e $y$ son las coordenadas cartesianas de cualquier punto de la recta.
El coeficiente $A$ es la segunda componente del vector director: $A=\text{v}_2}$
El coeficiente $B$ es la primera componente del vector director cambiada de signo: $B=-\text{v}_1}$
El coeficiente $C$ se calcula sustituyendo el punto conocido $P$ en la ecuación de la recta.

ecuacion implicita general o cartesiana de la recta en el espacio (en R3)

Por otro lado, ten en cuenta que, a parte de la ecuación implícita (o general), existen más formas de expresar analíticamente una recta: la ecuación vectorial, las ecuaciones paramétricas, la ecuación continua, la ecuación explícita y la ecuación punto-pendiente de una recta. Puedes consultar en qué consiste cada una de ellas en nuestra web.

Ejemplo de cómo calcular la ecuación implícita, general o cartesiana de la recta

Solo viendo la fórmula puede parecer que este tipo de ecuación de la recta resulta un poco complicado hallarla. Pero para que veas que es precisamente todo lo contrario vamos a ver cómo hallar la ecuación general (o implícita) de la recta mediante un ejemplo:

Determina la ecuación implícita de la recta que pasa por el punto $P$ y tiene $\vv{\text{v}}$ como vector director:

$\vv{\text{v}}= (2,3) \qquad P(5,-1)$

Como hemos visto en el apartado de arriba, la fórmula de la ecuación implícita de la recta es:

$Ax+By+C=0$

De modo que debemos encontrar los coeficientes A, B y C. Las incógnitas A y B se obtienen a partir de las coordenadas del vector director de la recta, ya que siempre se cumple la siguiente igualdad:

$\vv{\text{v}}= (-B,A)$

Por lo tanto, el coeficiente A es la segunda coordenada del vector, y el coeficiente B es la primera coordenada del vector cambiada de signo:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,3) \end{array} \right\}\longrightarrow \begin{array}{l}A=3 \\[2ex] B=-2 \end{array}$

Así que la ecuación implícita de la recta será de la siguiente forma:

$Ax+By+C=0 \ \xrightarrow{A=3 \ ; \ B=-2} \ 3x-2y+C=0$

Por tanto, solo nos queda averiguar el coeficiente C. Para ello, debemos sustituir el punto que sabemos que pertenece a la recta en su ecuación:

$P(5,-1)$

$3x-2y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 3\cdot 5-2\cdot (-1)+C=0$

Y ahora resolvemos la ecuación resultante:

$3\cdot 5-2\cdot (-1)+C=0$

$15+2+C=0$

$17+C=0$

$C=-17$

De manera que la ecuación implícita, general o cartesiana de la recta es:

$\bm{3x-2y-17=0}$

Hallar la ecuación implícita (general o cartesiana) a partir de la ecuación continua

Acabamos de ver una manera de encontrar la ecuación general de una recta. Sin embargo, existe otro método que es a partir de su ecuación continua. Veamos cómo se hace con un ejemplo:

Calcula la ecuación general (o implícita) de la siguiente recta definida mediante su ecuación continua:

$\cfrac{x-1}{-2}=\cfrac{y+4}{6}$

Primero de todo, multiplicamos en cruz las fracciones:

$(x-1)\cdot 6 = (y+4) \cdot (-2)$

En segundo lugar, resolvemos los paréntesis mediante la propiedad distributiva:

$6x-6=-2y-8$

Luego pasamos todos los términos al lado izquierdo de la ecuación:

$6x-6+2y+8=0$

Y, por último, agrupamos los términos y conseguimos así la ecuación general de la recta:

$\bm{6x+2y+2=0}$

Ejercicios resueltos de la ecuación implícita o general (o cartesiana)

Ejercicio 1

Escribe la ecuación general de la recta que pasa por el punto $P$ y tiene $\vv{\text{v}}$ como vector director:

$\vv{\text{v}}= (-1,2) \qquad P(4,0)$

Ver solución

La fórmula de la ecuación general de la recta es:

$Ax+By+C=0$

De modo que debemos encontrar A, B y C. Las variables A y B se obtienen a partir de las coordenadas del vector director de la recta, ya que siempre se cumple la siguiente igualdad:

$\vv{\text{v}}= (-B,A)$

Por lo tanto, el coeficiente A es la segunda coordenada del vector, y el coeficiente B es la primera coordenada del vector cambiada de signo:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (-1,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=1 \end{array}$

Así que la ecuación implícita de la recta será de la siguiente forma:

$Ax+By+C=0 \ \xrightarrow{A=2 \ ; \ B=1} \ 2x+y+C=0$

Por tanto, solo nos queda hallar el coeficiente C. Para ello, debemos sustituir en la ecuación de la recta el punto que sabemos que pertenece a la recta y resolver la ecuación resultante:

$P(4,0)$

$2x+y+C=0 \ \xrightarrow{x=4 \ ; \ y=0} \ 2\cdot 4+0+C=0$

$8+C=0$

$C=-8$

En definitiva, la ecuación implícita, general o cartesiana de la recta es:

$\bm{2x+y-8=0}$

Ejercicio 2

Calcula la ecuación cartesiana de la siguiente recta:

$\cfrac{x+3}{4}=\cfrac{y-2}{5}$

Ver solución

La ecuación está expresada en forma de ecuación continua, por lo que para hallar su ecuación implícita debemos multiplicar en cruz las fracciones y agrupar todos los términos en un solo miembro de la ecuación:

$\cfrac{x+3}{4}=\cfrac{y-2}{5}$

$(x+3)\cdot 5 = (y-2) \cdot 4$

$5x+15=4y-8$

$5x+15-4y+8=0$

$\bm{5x-4y+23=0}$

Ejercicio 3

Determina un punto de la siguiente recta y su vector director. La recta está expresada con su ecuación general:

$-x-3y+6= 0$

Ver solución

Las componentes del vector director de la recta se pueden conseguir a partir de los coeficientes A y B de la ecuación general de la recta: la primera componente del vector corresponde al coeficiente B cambiado de signo y la segunda componente del vector es igual al coeficiente A. Por tanto:

$\vv{\text{v}}= (-B,A)$

$\vv{\mathbf{v}}=\bm{(3,-1)}$

Por otra parte, para calcular un punto de la recta, debemos otorgar un valor a una variable. Por ejemplo, hacemos $x=0$ y resolvemos la ecuación resultante:

$-x-3y+6= 0 \ \xrightarrow{x \ = \ 0} \ -0 -3y+6=0$

$-3y +6 =0$

$-3y =-6$

$y =\cfrac{-6}{-3}$

$y =2$

De manera que el punto de la recta es:

$\bm{P(0,2)}$

Puede que hayas obtenido otro punto diferente, porque depende del valor que le des a la variable X (o a la variable Y), pero si has seguido el mismo procedimiento también es correcto. En cambio, el vector director de la recta sí que debe ser idéntico al calculado.

Ejercicio 4

Calcula la ecuación implicita de la recta que pasa por los siguientes dos puntos:

$A(4,-1) \qquad B(-2,3)$

Ver solución

En este caso no sabemos el vector director de la recta, por lo que primero debemos encontrar su vector director y luego la ecuación de la recta.

Para hallar el vector director de la recta basta con calcular el vector definido por los dos puntos dados:

$\vv{AB}=B-A= (-2,3)- (4,-1) = (-6,4)$

Y una vez sabemos el vector director de la recta, ya podemos determinar su ecuación implícita (o general o cartesiana) a partir de su fórmula:

$Ax+By+C=0$

Las incógnitas A y B se obtienen a partir de las coordenadas del vector director de la recta, ya que el coeficiente A es la segunda coordenada del vector, y el coeficiente B es la primera coordenada del vector cambiada de signo:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (-6,4) \end{array} \right\}\longrightarrow \begin{array}{l}A=4 \\[2ex] B=6 \end{array}$

Así que la ecuación implícita de la recta será de la siguiente forma:

$Ax+By+C=0 \ \xrightarrow{A=4 \ ; \ B=6} \ 4x+6y+C=0$

Por tanto, solo nos queda hallar el coeficiente C. Para ello, debemos sustituir en la ecuación de la recta un punto que sabemos que pertenece a la recta y resolver la ecuación resultante:

$A(4,-1)$

$4x+6y+C=0\ \xrightarrow{x=4 \ ; \ y=-1} \ 4\cdot 4+6\cdot (-1)+C=0$

$16-6+C=0$

$10+C=0$

$C=-10$

Finalmente, la ecuación implícita, general o cartesiana de la recta es:

$\bm{4x+6y-10=0}$

Ejercicio 5

Halla la ecuación implícita de la recta perpendicular a la recta $r$ y que pasa por el punto $P(2,2).$

$r: \; 3x-2y+4=0$

Ver solución

Dos rectas perpendiculares tienen vectores directores ortogonales entre sí, por lo tanto, debemos encontrar el vector director de la recta $r$ y luego un vector perpendicular a él.

Las componentes del vector director de la recta $r$ se pueden conseguir a partir de los coeficientes A y B de la ecuación general de la recta: la primera componente del vector corresponde al coeficiente B cambiado de signo y la segunda componente del vector es igual al coeficiente A.

$r: \; 3x-2y+4=0$

$\vv{\text{v}}= (-B,A)$

$\vv{\text{v}}_r=(2,3)$

Ahora hay que encontrar un vector perpendicular. Para ello, simplemente debemos intercalar las coordenadas del vector y cambiar de signo a una de ellas:

$\vv{\text{v}}_\perp=(-3,2)$

De manera que ese será el vector director de la recta perpendicular a $r.$

Y una vez sabemos el vector director de la recta, ya podemos determinar su ecuación implícita (o general o cartesiana) a partir de su fórmula:

$Ax+By+C=0$

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (-3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=3 \end{array}$

Así que la ecuación implícita de la recta será de la siguiente forma:

$Ax+By+C=0 \ \xrightarrow{A=2 \ ; \ B=3} \ 2x+3y+C=0$

Por tanto, solo nos queda hallar el coeficiente C. Para ello, debemos sustituir en la ecuación de la recta un punto que sabemos que pertenece a la recta y resolver la ecuación resultante:

$P(2,2)$

$2x+3y+C=0\ \xrightarrow{x=2 \ ; \ y=2} \ 2\cdot 2+3\cdot 2+C=0$

$4+6+C=0$

$10+C=0$

$C=-10$

De modo que la ecuación implícita, general o cartesiana de la recta es:

$\bm{2x+3y-10=0}$

Ecuación implícita o general (o cartesiana) de la recta

¿Qué es la ecuación implícita, general o cartesiana de la recta?

Fórmula de la ecuación implícita, general o cartesiana de la recta

Ejemplo de cómo calcular la ecuación implícita, general o cartesiana de la recta

Hallar la ecuación implícita (general o cartesiana) a partir de la ecuación continua

Ejercicios resueltos de la ecuación implícita o general (o cartesiana)

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

1 comentario en “Ecuación implícita o general (o cartesiana) de la recta”

Deja un comentario Cancelar respuesta