Pendiente de una recta (fórmula)

En esta página encontrarás la explicación más detallada sobre la pendiente de una recta: cuál es su fórmula, ejemplos de cómo se calcula, qué significa el concepto de pendiente de una recta,… También podrás ver cómo se puede identificar fácilmente la pendiente de una recta a partir de su ecuación y, además, podrás practicar con ejercicios resueltos paso a paso.

Fórmula de la pendiente de una recta

La pendiente de una recta es igual al desplazamiento vertical entre dos puntos dividido por el desplazamiento horizontal entre esos dos mismos puntos.

Es decir, dados dos puntos de un recta:

P_1(x_1,y_1) \qquad P_2(x_2,y_2)

La fórmula de la pendiente de una recta es:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}

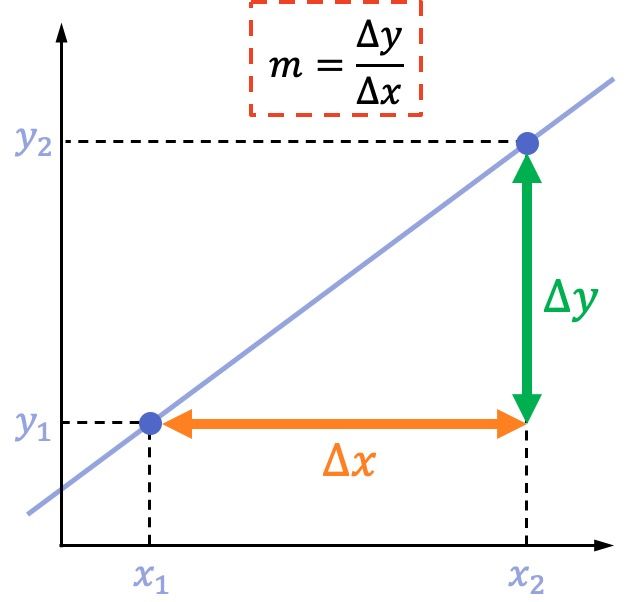
cual es la pendiente de una la recta

Ejemplo de cómo calcular la pendiente de una recta a partir de dos puntos

A continuación vamos a ver un ejemplo de cómo se calcula la pendiente de una recta con la fórmula:

  • Calcula la pendiente de la recta que pasa por los siguientes dos puntos:

P_1(3,1) \qquad P_2(5,7)

Para hallar la pendiente de esta recta, simplemente se debe aplicar su fórmula:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}

Por tanto, la pendiente de la recta es igual a 3.

Hallar la pendiente de una recta a partir de su ecuación

En el apartado de arriba acabamos de ver cómo determinar la pendiente de una recta numéricamente. Sin embargo, no siempre hace falta hacer cálculos, sino que también se puede identificar su valor a partir de la ecuación de una recta. Cada tipo de ecuación es diferente, por lo que analizaremos cada caso por separado.

Pendiente dada la ecuación explícita de la recta

La ecuación explícita de la recta sigue la siguiente expresión:

y =\color{blue}\bm{m}\color{black}x+n

Entonces, el parámetro m corresponde a la pendiente de la recta.

Pendiente dada la ecuación punto-pendiente de la recta

La fórmula de la ecuación punto – pendiente de la recta es la siguiente:

y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)

Igual que antes, el coeficiente m corresponde a la pendiente de la recta.

Pendiente dada la ecuación implícita de la recta

Dada la ecuación implícita de la recta (también conocida como ecuación general o cartesiana):

Ax+By+C=0

La pendiente de la recta se puede encontrar haciendo:

m=-\cfrac{A}{B}

Pendiente dado el vector director de la recta

El vector director de la recta es el vector que marca su dirección. Entonces, si el vector director de una recta es:

\vv{\text{v}}= (\text{v}_1,\text{v}_2)

La pendiente de dicha recta es:

m=\cfrac{\text{v}_2}{\text{v}_1}

Pendiente dado un ángulo

Por último, si una recta forma un ángulo \alpha con la parte positiva del eje de las abscisas (eje X), su pendiente es equivalente a la tangente del ángulo:

m = \text{tg}(\alpha)

Significado de la pendiente de una recta

Con toda la información de arriba ya sabemos completamente cómo sacar la pendiente de una recta. Pero realmente… ¿qué significa la pendiente de una recta?

La pendiente de una recta indica las unidades verticales que sube la recta por cada unidad horizontal de la gráfica.

Por ejemplo, en la representación de la siguiente recta puedes ver que avanza 2 unidades verticales por cada unidad horizontal, porque su pendiente es igual a 2.

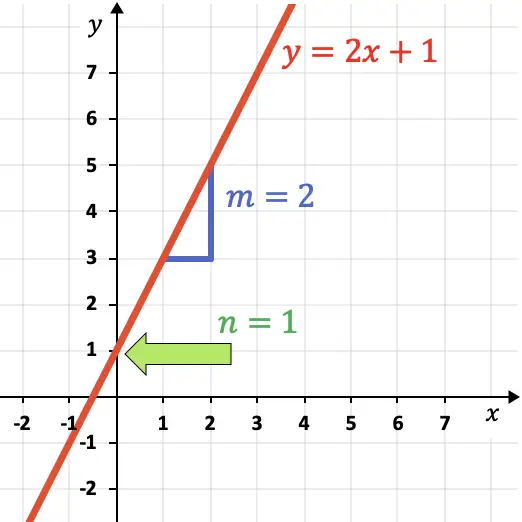
cual es la pendiente de una recta

Además, la pendiente de una recta también indica su inclinación:

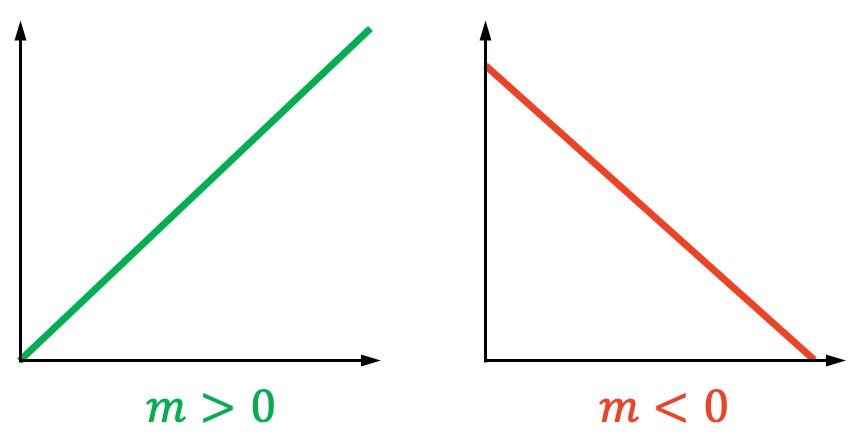
  • Si una recta es creciente (va hacia arriba), su pendiente es positiva.
  • Si una recta es decreciente (va hacia abajo), su pendiente es negativa.
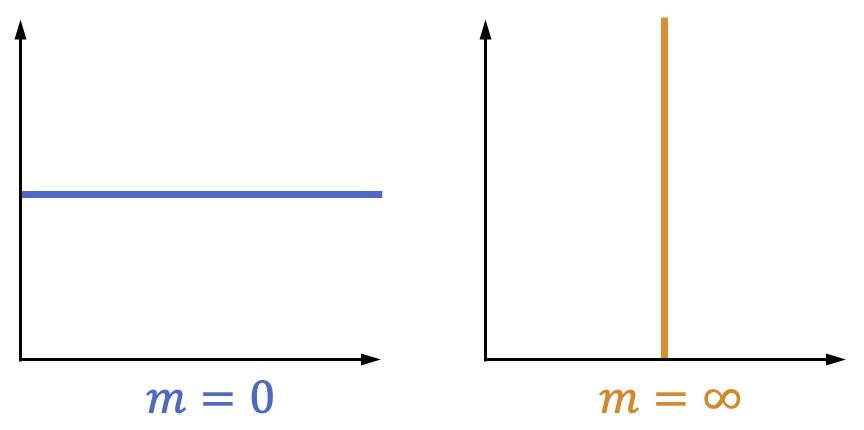
  • Si una recta es completamente horizontal, su pendiente es igual a 0.
  • Si una recta es totalmente vertical, su pendiente es equivalente a infinito.
pendiente de una recta positiva o negativa
pendiente de una recta nula o infinita

Posición relativa de las rectas

Por otro lado, también se puede conocer la posición relativa entre dos rectas a partir de las propiedades de las pendientes:

  • Si dos rectas tienen pendientes diferentes significa que son secantes, es decir, que se cortan en algún punto.
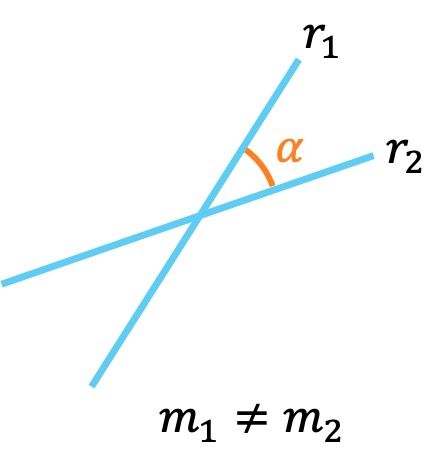
rectas secantes pendientes distintas

Además, se puede calcular el ángulo que forman las dos rectas a través de sus pendientes con la siguiente fórmula:

\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}

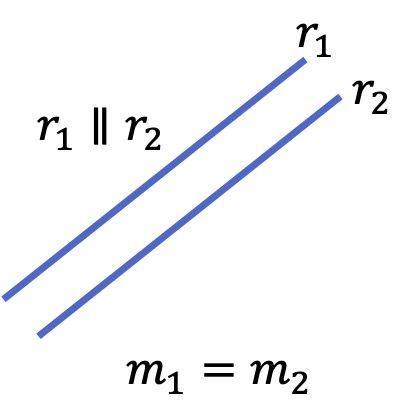
  • En segundo lugar, si dos rectas tienen la misma pendiente implica que son paralelas.
rectas paralelas pendientes iguales
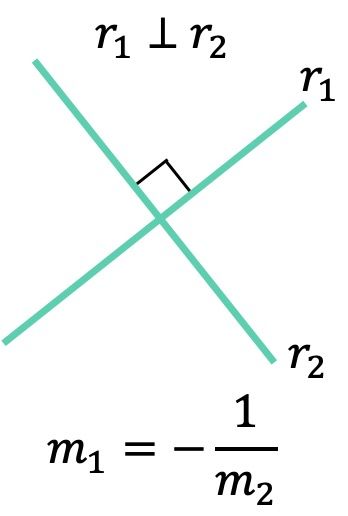
  • Por último, las pendientes de dos rectas perpendiculares u ortogonales (que forman 90º) cumplen la siguiente condición:
rectas perpendiculares pendientes opuestas

Esta es una forma de saber si dos rectas son paralelas o perpendiculares entre sí, sin embargo, existen más métodos e incluso algunos son más rápidos. Para saber más puedes ir a la explicación de la perpendicularidad y el paralelismo entre rectas. Además, en estas páginas también está explicado cómo encontrar una recta perpendicular (o paralela) a otra.

Ejercicios resueltos de la pendiente de una recta

Ejercicio 1

Halla la pendiente de la recta que pasa por los siguientes dos puntos:

P_1(5,6) \qquad P_2(8,3)

Para calcular la pendiente de la recta debemos utilizar la fórmula:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}

 

Ejercicio 2

Calcula la pendiente de la recta que pasa por los siguientes dos puntos:

P_1(-3,1) \qquad P_2(-2,-4)

Para encontrar la pendiente de la recta debemos usar la fórmula:

m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}

 

Ejercicio 3

¿Cuál es la pendiente de cada recta?

\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}

A) La recta está expresada en forma de ecuación implícita, por lo que su pendiente es 2 (el término que acompaña a la x).

B) La recta está definida mediante su ecuación punto-pendiente, por lo tanto, su pendiente es 4 (el número de delante del paréntesis).

C) La recta se encuentra en forma de ecuación implícita, así que su pendiente es:

m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}

D) La recta está definida en forma de ecuaciones paramétricas, de modo que primero debemos hallar su vector director y con él ya podremos calcular la pendiente de la recta. Así pues, las componentes del vector director son los términos que acompañan al coeficiente t:

\vv{\text{v}} = (-1,2)

Y una vez conocemos el vector director de la recta, podemos determinar la pendiente de la recta:

m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}

 

Ejercicio 4

Determina la pendiente de cada recta que está representada gráficamente:

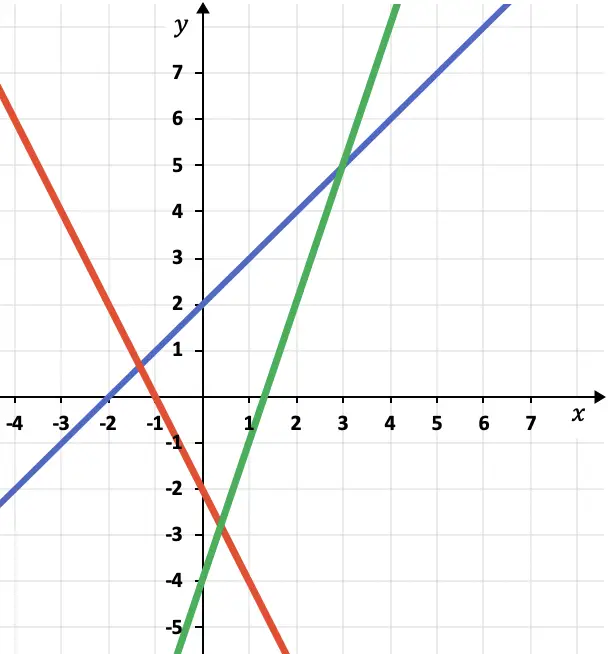
ecuacion explicita de la recta ejercicio resuelto paso a paso

Recta azul

La recta azul aumenta una Y por cada X, por lo tanto, su pendiente es igual a 1.

m=1

Recta verde

La recta verde aumenta tres Y por cada X, por lo que su pendiente es 3.

m=3

Recta roja

La recta roja disminuye dos Y por cada X, por lo tanto, su pendiente es equivalente a -2.

m=-2

 

14 comentarios en “Pendiente de una recta (fórmula)”

  3. PEDRO MORALES

    MUY BUENA EXPLICACIÓN GRÁFICA, BIEN EXPUESTO EXPLICADO,
    FELICITACIONES, GENEREN TEMAS SIMILARES DE MATEMATICAS.

    Responder
    1. Geometría Analítica

      ¡Muchas gracias Pedro! ¡Se agradecen mensajes de felicitación como este!

      Por si te interesa, también tenemos más páginas webs con otros temas de matemáticas:

      • – matricesydeterminantes.com
      • – polinomios.org
      • – ejerciciosecuaciones.com
      • – funciones.xyz
      • – areasyvolumenes.net
      • – probabilidadyestadistica.net
  5. Rodolfo

    muchas gracias no habia entendido estos temas y voy en bachillerato y me ayudaron a terminar de entenderlos y no solo aprender la formula, muy claro las explicaciones, gracias asi ayudaran a que no repruebe mi materia

    Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio