▷ ¿Qué son los Vectores Ortogonales (o Perpendiculares)?

En esta página encontrarás todo lo relacionado con los vectores perpendiculares (u ortogonales): qué son, cuándo dos vectores son ortogonales, cómo encontrar un vector perpendicular a otro, las propiedades de los vectores perpendiculares,… Además, podrás ver varios ejemplos y ejercicios resueltos de vectores perpendiculares u ortogonales.

Índice

¿Qué son dos vectores perpendiculares u ortogonales?

En matemáticas, dos vectores son ortogonales (o perpendiculares) cuando forman un ángulo recto (90º) entre sí.

En la siguiente representación gráfica puedes ver dos vectores perpendiculares:

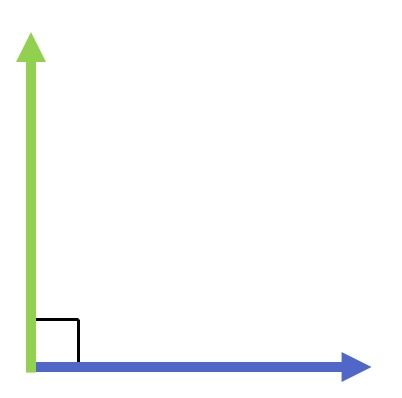
cuando se dice que dos vectores son perpendiculares u ortogonales

Por otro lado, la perpendicularidad de dos vectores depende únicamente de su dirección, y no de su módulo (o magnitud) ni, evidentemente, de su sentido. Es decir, dos vectores serán perpendiculares si forman un ángulo de 90 grados, independientemente de si tienen la misma longitud o no.

¿Cómo saber si dos vectores son ortogonales o perpendiculares?

Como acabamos de ver, gráficamente es muy fácil ver si dos vectores son perpendiculares. Sin embargo, también se puede determinar si dos vectores son ortogonales sin representarlos en un gráfico:

Numéricamente, dos vectores son ortogonales o perpendiculares cuando su producto escalar es igual a cero (0).

Por ejemplo, vamos a demostrar que los siguientes dos vectores son perpendiculares sin representarlos gráficamente:

$\vv{\text{u}}=(3,2) \qquad\vv{\text{v}}=(-2,3)$

Para verificar que son vectores perpendiculares (u ortogonales), aplicamos la fórmula del producto escalar:

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(3,2)\cdot (-2,3) \\[1.5ex]&=3\cdot (-2) + 2 \cdot 3 \\[1.5ex] & = -6+6 \\[1.5ex] & =\bm{0} \end{aligned}$

El resultado del producto escalar de los dos vectores es nulo, por lo tanto, se trata de dos vectores ortogonales (o perpendiculares) entre sí.

$\vv{\text{u}}\bm{\perp} \vv{\text{v}}$

Fíjate que se indica que dos vectores son perpendiculares mediante el símbolo $\bm{\perp}}.$

Por lo tanto, el producto escalar entre dos vectores perpendiculares es nulo. Sin embargo, el producto vectorial de dos vectores (otro tipo de multiplicación entre vectores) da todo lo contrario: un vector perpendicular a los otros dos. Por tanto, es importante saber distinguir los dos tipos de operaciones, puedes ver las diferencias entre ellas en las propiedades del producto vectorial.

¿Cómo se calcula un vector perpendicular u ortogonal a otro?

La manera más fácil de calcular un vector perpendicular a otro en el plano (en R2) es intercalar las dos coordenadas del vector y, además, cambiar el signo a una.

Y para obtener un vector perpendicular a otro en el espacio (en R3) se deben intercalar dos coordenadas entre sí, luego cambiar de signo a una de ellas y, finalmente, hacer cero la coordenada restante.

Para que puedas ver las diferencias que hay en cómo calcular un vector ortogonal a otro dependiendo de si tienen 2 o 3 coordenadas, vamos a resolver un ejercicio con cada tipo de vectores.

Hallar un vector perpendicular u ortogonal en el plano cartesiano

Determina un vector perpendicular al siguiente vector bidimensional:

$\vv{\text{v}}=(4,1)$

Como se trata de un vector con solo dos componentes, para obtener un vector perpendicular debemos alternar sus componentes y negar una de ellas:

$\vv{\mathbf{u}}\bm{=(-1,4)}$

Podemos comprobar a partir de la fórmula del producto escalar que efectivamente son vectores perpendiculares:

$\vv{\text{v}} \cdot \vv{\text{u}}=(4,1)\cdot (-1,4) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Determinar un vector perpendicular u ortogonal en el espacio cartesiano

Calcula un vector ortogonal al siguiente vector tridimensional:

$\vv{\text{v}}=(2,3,-1)$

En este caso tenemos un vector con tres componentes, así que para obtener un vector perpendicular debemos alternar dos de sus componentes, cambiar de signo a una de ellas y convertir en cero la coordenada restante:

$\vv{\mathbf{u}}\bm{=(3,-2,0)}$

Se puede verificar con la fórmula del producto escalar que realmente son vectores ortogonales:

$\vv{\text{v}} \cdot \vv{\text{u}}=(2,3,-1)\cdot (3,-2,0) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

Propiedades de los vectores perpendiculares y ortogonales

Los vectores perpendiculares tienen las siguientes características:

Relación simétrica: si un vector es perpendicular a otro vector, ese vector también es perpendicular al primer vector.

$\vv{\text{u}} \bm{\perp} \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \bm{\perp} \vv{\text{u}}$

Propiedad irreflexiva: obviamente, ningún vector puede ser perpendicular a sí mismo.

$\vv{\text{v}} \ \cancel{\bm{\perp}}} \ \vv{\text{v}}$

En geometría euclidiana (en R2), cualquier par de vectores que son perpendiculares a un tercer vector deben ser necesariamente paralelos. O dicho de otra forma, si un vector es perpendicular a otro vector y este vector es a la vez perpendicular a un tercer vector, el primer y el último vector son paralelos. Eso es debido al quinto postulado de Euclides.

Por otro lado, también debes saber que gracias a estas propiedades se puede utilizar la regla del sacacorchos. Esta técnica sirve para calcular fácilmente un tipo de operación vectorial que, si no fuese por esta regla, se tardaría mucho en resolver. Puedes ver en qué consiste haciendo click en la explicación de la regla del sacacorchos.

Conceptos relacionados con los vectores perpendiculares u ortogonales

Existen dos tipos de vectores muy parecidos a los vectores perpendiculares: los vectores normales y los vectores ortonomarles. Aunque todos ellos están relacionados entre sí, queremos dejar claro en qué se diferencian para evitar posibles confusiones.

Un vector normal es un vector perpendicular a un plano. De modo que también puede incluirse dentro del concepto de ortogonalidad de un vector, pero en este caso es perpendicular hacia un plano en vez de hacia otro vector.

Por otra parte, dos vectores ortonormales son dos vectores que son ortogonales entre sí y que, además, son vectores unitarios (de módulo igual a 1).

Finalmente, también cabe destacar que es muy frecuente utilizar bases ortogonales (bases vectoriales formadas por vectores perpendiculares entre sí) e incluso bases ortonormales. De hecho, el sistema de coordenadas cartesiano es una base ortonormal.

2 comentarios en “Vectores perpendiculares u ortogonales”

Rocimar
11/11/2021 a las 18:42

Diagrama un vector a con cualquiera que se ubique perpendicular en un plano horizontal

Responder
1. Geometría Analítica
  15/11/2021 a las 10:48
  
  Hola Rocimar,
  
  Un vector será perpendicular a un plano horizontal cuando sea múltiple de (0,0,1), por lo tanto, debes hallar un vector perpendicular a este. En este caso el vector perpendicular puede tener cualquier número de primera y segunda componente, pero la tercera componente debe ser obligatoriamente cero.
  Finalmente, puedes ver cómo se representa un vector en el post correspondiente de geometriaanalitica.info.