En esta página encontrarás todo sobre las rectas perpendiculares: qué son, cuándo dos rectas son perpendiculares, cómo calcular una recta perpendicular a otra, sus propiedades,… Además, podrás ver ejemplos y podrás practicar con ejercicios resueltos paso a paso.
Índice
¿Qué son dos rectas perpendiculares?
En matemáticas, dos rectas son perpendiculares cuando se cortan en un punto formando cuatro ángulos rectos (de 90º) iguales.
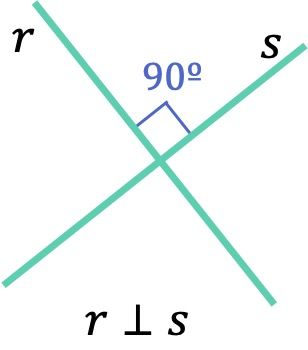
Además, los vectores directores de dos rectas perpendiculares deben ser también perpendiculares.
Se suele indicar la perpendicularidad de dos rectas con el símbolo
Por otra parte, recuerda que en el plano existen 4 posibilidades dentro del concepto de posición relativa entre dos rectas: dos rectas pueden ser secantes, perpendiculares, coincidentes o paralelas. Si quieres puedes consultar qué significa cada tipo de recta en nuestra web.
¿Cómo saber si dos rectas son perpendiculares?
Existen dos maneras de determinar cuándo dos rectas son perpendiculares, a partir de sus vectores directores o mediante sus pendientes. A continuación tienes la explicación de los dos métodos, aunque sirven para lo mismo te recomendamos que sepas hacer los 2 procedimientos ya que cada uno depende de la forma en la que estén expresadas las rectas.
A partir de los vectores directores de las rectas
Una manera de saber cuándo dos rectas son perpendiculares es con los vectores directores de las rectas en cuestión. Recuerda que el vector director es aquel vector que indica la dirección de una recta.
Los vectores directores de dos rectas perpendiculares también son ortogonales entre sí. Por tanto, si el producto escalar de los vectores directores de dos rectas es igual a 0, significa que las rectas son perpendiculares.
Veamos cómo se determina la perpendicularidad de dos rectas a partir de un ejemplo:
Ambas rectas están expresadas en forma de ecuaciones paramétricas, de modo que las componentes del vector director de cada recta son los números de delante del parámetro
Una vez conocemos el vector director de cada recta, comprobamos si son perpendiculares calculando el producto entre los vectores:
El producto escalar de los dos vectores da como resultado cero, por lo que las rectas son perpendiculares.
A partir de las pendientes de las rectas
Otra forma de determinar si dos rectas son perpendiculares es utilizando sus pendientes. Recuerda que la pendiente de una recta es el coeficiente de la ecuación explícita y de la ecuación punto-pendiente de una recta.
Y la pendiente de una recta también se puede obtener de los coeficientes y
de la ecuación implícita (o general) de una recta:
Así pues, las pendientes de dos rectas perpendiculares son inversas y de signo contrario, es decir, siempre se cumple la siguiente igualdad:
De modo que si el producto de las pendientes de dos rectas distintas es igual a -1, implica que las rectas son perpendiculares:
Por ejemplo, las siguientes dos rectas son perpendiculares:
Se puede demostrar que son dos rectas perpendiculares entre sí a partir de sus pendientes. La pendiente de cada recta es:
Ahora multiplicamos las pendientes:
El producto entre las dos pendientes es equivalente a -1, con lo que efectivamente se trata de dos rectas perpendiculares entre sí.
¿Cómo calcular una recta perpendicular a otra?
Aunque puede parecer algo difícil de hacer, encontrar una recta perpendicular a otra es bastante sencillo, para ello solo se necesita un vector director perpendicular a la recta y un punto que pertenezca a la recta.
La única dificultad es que, al igual que antes, el procedimiento depende del tipo de ecuación en el que estén expresadas las rectas. Porque se puede calcular una recta perpendicular a otra a partir de los vectores directores o de las pendientes.
A partir del vector director de la recta
Se puede hallar una recta perpendicular a otra recta dada mediante su vector director. Veamos cómo se hace con un ejemplo:
- Calcula la recta perpendicular a la recta
que pasa por el punto
. Siendo la recta
Lo primero que debemos hacer es identificar el vector director de la recta. En este caso la recta está definida en forma de ecuación general (o implícita), por lo tanto, las coordenadas cartesianas del vector director de la recta se puede conseguir con los coeficientes A y B de la recta:
Y una vez sabemos el vector director de la recta, debemos calcular un vector perpendicular a él. Para ello, simplemente tenemos que intercalar las coordenadas del vector y cambiar de signo a una de ellas (la que quieras):
De modo que ahora ya conocemos el vector director de la recta. Así que la ecuación implícita de la recta será de la siguiente forma:
Por tanto, solo nos falta determinar el parámetro C. Para ello, sustituimos el punto que pertenece a la recta en su ecuación y resolvemos la ecuación resultante:
En conclusión, la ecuación de la recta perpendicular es:
A partir de la pendiente de la recta
Otra manera de averiguar una recta perpendicular a una determinada recta es a partir de su pendiente. Veamos cómo se resuelve este tipo de problema a través de un ejemplo:
- Calcula la recta perpendicular a la recta
que pasa por el punto
. Siendo la recta
La pendiente de la recta es:
Una vez sabemos la pendiente de la recta, debemos encontrar la pendiente de la recta perpendicular. Como hemos visto en los apartados de arriba, las pendientes de dos rectas perpendiculares son inversas y cambiadas de signo. Por tanto, para determinar la pendiente de la recta perpendicular debemos invertir la pendiente hallada y cambiarla de signo:
De forma que la ecuación explícita de la recta perpendicular será de la siguiente forma:
Por último, calculamos la ordenada en el origen de la recta perpendicular sustituyendo las coordenadas del punto en la ecuación de la recta:
En definitiva, la ecuación de la recta perpendicular es:
Propiedades de las rectas perpendiculares
Todas las rectas perpendiculares tienen las siguientes características:
- Relación simétrica: si una recta es perpendicular a otra recta, esa recta también es perpendicular a la primera recta.
- Propiedad irreflexiva: obviamente, ninguna recta puede ser perpendicular a sí misma.
- Teorema: en geometría euclidiana (en R2), cualquier par de rectas que son perpendiculares a una tercera recta deben ser necesariamente paralelas. O dicho de otra forma, si una recta es perpendicular a otra recta y esta recta es a la vez perpendicular a una tercera recta, la primera y la última recta son paralelas.
Ejercicios resueltos de rectas perpendiculares
Ejercicio 1
¿Cuáles de las siguientes rectas son perpendiculares a la recta ?
La pendiente de la recta es 3:
Y las pendientes de dos rectas perpendiculares son inversas y de signo contrario, por tanto, la pendiente de cualquier recta perpendicular a la recta debe ser:
De manera que las rectas perpendiculares a la recta son aquellas que tienen la pendiente igual a
. Es decir, las rectas
y
Ejercicio 2
Determina si las siguientes dos rectas son perpendiculares:
La recta está expresada en forma de ecuación paramétrica, de modo que las componentes del vector director de dicha recta son los números de delante del parámetro
Por otro lado, la recta está definida en forma de ecuación continua, por lo que las coordenadas de su vector director son los números de los denominadores:
Una vez conocemos el vector director de cada recta, podemos verificar si son perpendiculares calculando el producto de los dos vectores:
El producto escalar de los dos vectores da diferente de cero, por tanto, las rectas no son perpendiculares.
Ejercicio 3
Halla la recta perpendicular a la recta que pasa por el punto
. Siendo la recta
Lo primero que debemos hacer es identificar el vector director de la recta. En este caso la recta está definida en forma de ecuación general (o implícita), por lo tanto, su vector director es:
Una vez conocemos el vector director de la recta, debemos calcular un vector perpendicular a él. Para ello, simplemente debemos intercalar las coordenadas del vector y cambiar de signo a una de ellas (la que quieras):
Así que la ecuación ecuación implícita de la recta será de la siguiente forma:
Por tanto, solo nos falta determinar la incógnita C. Para ello, sustituimos el punto por el que pasa la recta en su ecuación:
Finalmente, la ecuación de la recta perpendicular es:
Ejercicio 4
Encuentra la ecuación punto-pendiente de la recta perpendicular a la recta que pasa por el punto
. Siendo la recta
La pendiente de la recta es:
Una vez sabemos la pendiente de la recta, debemos encontrar la pendiente de la recta perpendicular. Para ello, solamente debemos invertir la pendiente hallada y cambiarla de signo:
Por último, solo nos queda sustituir la pendiente encontrada y las coordenadas del punto en la ecuación punto-pendiente de la recta:
Ejercicio 5
La recta pasa por los puntos (2,1) y (4,2), y la recta
pasa por los puntos (-1,2) y (1,-2). Determina si se trata de dos rectas perpendiculares o no.
Para comprobar si son dos rectas perpendiculares, calcularemos sus pendientes y luego veremos si cumplen la relación de perpendicularidad. Recuerda que la fórmula de la pendiente de una recta es:
La pendiente de la recta es:
La pendiente de la recta es:
Para realizar la comprobación de la perpendicularidad de las dos rectas, debemos ver si la pendiente de una recta es el inverso cambiado de signo de la otra pendiente. En este caso, las dos pendientes son inversas y además son de signo contrario, así que las dos rectas son perpendiculares entre sí.
Ejercicio 6
Calcula el valor de para que las siguientes dos rectas sean perpendiculares:
Las dos rectas están expresadas en forma de ecuación implícita (o general), y el vector director de una ecuación implícita de la recta es:
Por tanto, el vector director de cada recta sería:
Para que dos rectas sean perpendiculares, el producto escalar de sus vectores directores debe ser nulo. Por lo tanto, aplicaremos esta condición para hallar el valor de la incógnita

Excelente información y ejercicios. Me gustaria que subieran ejercicios de rectas pertenecientes a R3
¡Muchas gracias Alejandro! Lo apunto para una futura actualización. 🙂