▷ ¿Cómo saber si 3 (o más) puntos están alineados? ✅

En esta página encontrarás la explicación de qué son los puntos alineados. También verás todos los métodos que hay para determinar si 3 (o más) puntos están alineados. Y, además, hallarás varios ejemplos e incluso ejercicios resueltos para que puedas practicar.

Índice

¿Qué significa que los puntos están alineados?

En geometría analítica, tres o más puntos están alineados si todos son de la misma recta, es decir, si se pueden unir trazando una línea recta entre ellos.

Evidentemente, 2 puntos siempre estarán alineados, ya que siempre se puede trazar una recta entre dos puntos. Sin embargo, tres puntos no tienen por qué estar en una misma línea. Principalmente, existen dos métodos para saber si 3 o más puntos están alineados:

Método de los vectores: consiste en ver si los vectores que forman los puntos son proporcionales.
Método de la ecuación de la recta: se basa en averiguar si los puntos pertenecen a una misma recta.

A continuación tienes la explicación de cada procedimiento y con ejemplos para que puedas decidir cuál te va mejor.

Cómo saber si 3 (o más) puntos están alineados con el método de los vectores

Dados tres puntos cualesquiera:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Los tres puntos están alineados si los vectores $\vv{AB}$ y $\vv{BC}$ tienen la misma dirección, es decir, si sus componentes son proporcionales.

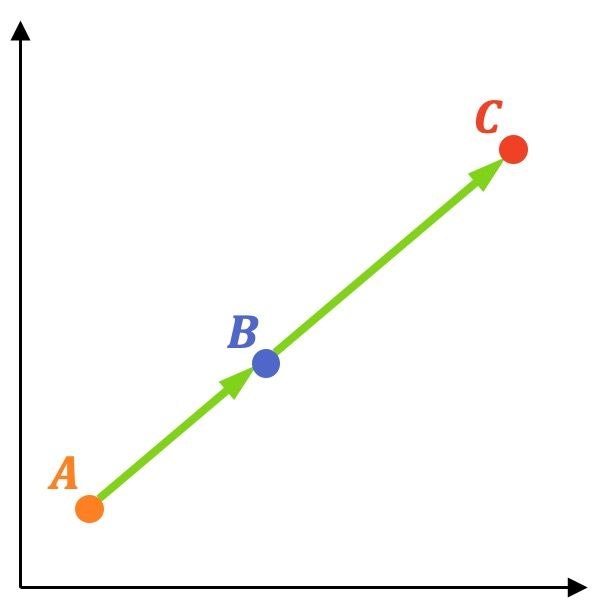
Veamos un ejemplo de cómo se hace:

Determina si los siguientes 3 puntos están alineados:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

En primer lugar, calculamos los vectores entre los puntos. Calculando dos vectores diferentes es suficiente:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

Y luego comprobamos si las coordenadas de los vectores son proporcionales:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Al dividir las componentes X y las componentes Y de los dos vectores obtenemos el mismo resultado (-2), por lo tanto, los vectores tienen la misma dirección y, en consecuencia, los puntos están alineados.

Este método también se puede utilizar para saber si tres o más puntos está alineados en el espacio (en R3), lo único que debemos añadir es la comprobación de que la tercera componente de los dos vectores (componente Z) también sea proporcional.

Si te está siendo útil este artículo, seguramente también te interese saber cómo se calcula el punto medio entre dos puntos, ya que, evidentemente, hallar el punto medio de 2 puntos es una forma de determinar un tercer punto alineado con los otros dos puntos. Puedes ver cómo se hace en la página del enlace, además, también podrás ver ejemplos y ejercicios resueltos paso a paso.

Cómo averiguar si 3 (o más puntos) están alineados con el método de la ecuación de la recta

Como acabamos de ver en el apartado anterior, una manera de estudiar la alineación de 3 o más puntos es a través de los vectores que se pueden formar entre ellos. Pues otro método es a partir de la ecuación de una recta:

Dados tres puntos cualesquiera:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Los tres puntos están alineados si todos ellos pertenecen a la misma recta. Por lo tanto, para hallar si tres o más puntos están alineados se deben seguir los siguientes pasos:

Encontrar la ecuación de la recta que pasa por dos de los tres puntos.
Comprobar si el tercer punto también pertenece a la recta. En ese caso significa que los 3 puntos están alineados, por contra, si no se cumple la condición implica que los puntos no están alineados.

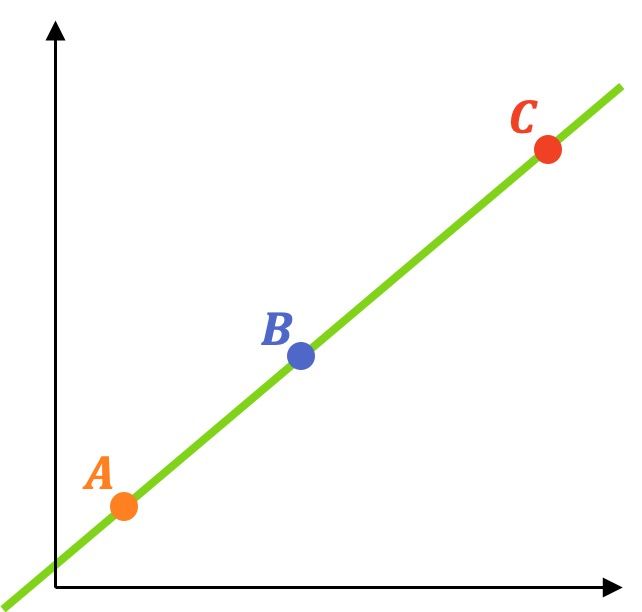
A modo de ejemplo, vamos a resolver un ejercicio mediante este método:

Comprueba que los siguientes 3 puntos están alineados:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Primero de todo, debemos calcular la ecuación de la recta que pasa por los puntos A y B. Así que hallamos el vector director de la recta:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Ahora debemos construir la ecuación de la recta, puedes escoger el tipo que quieras: paramétricas, implícita, general, etc. Pero en este caso nosotros usaremos la ecuación continua. De modo que la ecuación continua de la recta que pasa por el punto A y el punto B será:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Una vez tenemos la ecuación de la recta, debemos verificar si el otro punto también pertenece a la misma recta. Para ello, sustituimos las coordenadas del punto C en la ecuación de la recta:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Hemos obtenido una igualdad, de modo que el punto satisface la ecuación de la recta. Y, por tanto, los 3 puntos son colineales.

Cabe destacar que un conjunto de puntos alineados no tienen porqué ser equidistantes, es decir, la distancia entre varios puntos alineados puede ser distinta. Puedes ver la diferencia entre los dos conceptos en la explicación de la distancia entre dos puntos (geometría), donde, además, podrás ver ejemplos y ejercicios resueltos paso a paso.

Ejercicios resueltos de puntos alineados

Ejercicio 1

Determina si los siguientes 3 puntos están alineados:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Ver solución

Podemos escoger cualquier de método de los dos que hemos visto para resolver el problema. En este caso utilizaremos el método de los vectores.

Primero de todo, calculamos los vectores entre los puntos:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

Y ahora verificamos si las coordenadas cartesianas de los vectores son proporcionales:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Al dividir las componentes X y las componentes Y de los dos vectores entre sí obtenemos el mismo resultado (-4), por lo tanto, los vectores tienen la misma dirección. Hecho que indica que los puntos están alineados.

Ejercicio 2

Dados 3 puntos:

$A(6,3) \quad B(4,-3) \quad C(4,5)$

Determina cuáles están alineados con los siguientes dos puntos:

$D(3,-1) \quad E(2,1)$

Ver solución

En este caso utilizaremos el método de la ecuación de la recta, de este modo nos ahorraremos algunos cálculos.

Así que calculamos la ecuación continua de la recta que pasa por los puntos D y E:

$\vv{DE} = E-D = (2,1) - (3,-1) = (-1,2)$

$\cfrac{x-3}{-1}=\cfrac{y+1}{2}$

Y ahora comprobamos qué puntos cumplen la ecuación de la recta, y por tanto están alineados con los puntos D y E, y cuáles no.

Comprobamos el punto A:

$\cfrac{6-3}{-1}=\cfrac{3+1}{2}$

$\cfrac{3}{-1}=\cfrac{4}{2}$

$-3\neq 2$

La ecuación de la recta no se cumple, por lo que el punto A no está alineado con los puntos D y E.

Verificamos ahora el punto B:

$\cfrac{4-3}{-1}=\cfrac{-3+1}{2}$

$\cfrac{1}{-1}=\cfrac{-2}{2}$

$-1= -1$

En este caso la ecuación de la recta sí que se cumple, con lo que el punto B es colineal con los puntos D y E.

Y, por último, repetimos el proceso con el punto C:

$\cfrac{4-3}{-1}=\cfrac{5+1}{2}$

$\cfrac{1}{-1}=\cfrac{6}{2}$

$-1\neq 3$

La ecuación de la recta no se cumple, de manera que el punto C no está alineado con los puntos D y E.

Ejercicio 3

Halla el valor de la incógnita $k$ para que los siguientes 3 puntos estén alineados:

$A(k,5) \quad B(-1,-4) \quad C(k-1,2)$

Ver solución

En este caso utilizaremos el método de los vectores.

Por lo que intentamos calcular los vectores entre los puntos:

$\vv{AB} = B - A = (-1,-4)- (k,5) = (-1-k,-9)$

$\vv{BC} = C-B =(k-1,2)- (-1,-4)= (k,6)$

Para que se cumpla la colinealidad de los tres puntos, las coordenadas de los dos vectores deben ser proporcionales. Así que aplicamos esta condición:

$\cfrac{-1-k}{k} = \cfrac{-9}{6}$