Fórmula de la distancia entre dos puntos (geometría)

En esta página encontrarás cómo se calcula la distancia entre dos puntos en geometría (fórmula). También podrás ver ejemplos y, además, practicar con ejercicios resueltos de la distancia entre dos puntos.

¿Cuál es la fórmula de la distancia entre dos puntos?

La distancia entre dos puntos es igual a la longitud del segmento que los une. Por lo tanto, en matemáticas, para determinar la distancia entre dos puntos diferentes se deben calcular los cuadrados de las diferencias entre sus coordenadas y luego hallar la raíz de la suma de dichos cuadrados.

Es decir, la fórmula que sirve para calcular qué distancia hay entre dos puntos diferentes en el plano cartesiano es la siguiente:

Dadas las coordenadas de dos puntos distintos:

A(x_1,y_1) \qquad \qquad B(x_2,y_2)

La fórmula de la distancia entre dos puntos es:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}

Esta fórmula proviene del módulo de un vector. De hecho, lo que estamos haciendo con está fórmula en realidad es calcular el módulo del vector que queda determinado por los dos puntos en cuestión. Puedes saber más al respecto en la explicación de cuál es el módulo de un vector.

Por otro lado, en geometría analítica la demostración de la fórmula de la distancia entre dos puntos también se puede hacer a partir del teorema de Pitágoras:

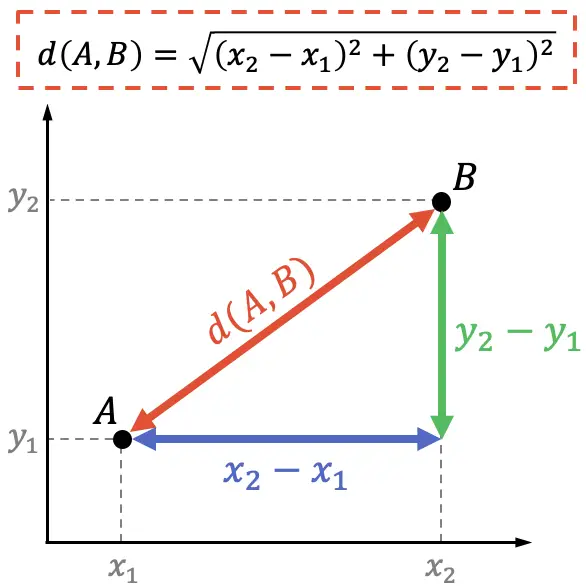
formula de la distancia entre dos puntos

El teorema de Pitágoras dice que el cuadrado de la hipotenusa de un triángulo rectángulo es equivalente a la suma de los cuadrados de sus catetos, por lo tanto:

\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2

Y para obtener la fórmula solo tenemos que despejar la distancia entre los 2 puntos:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}

Finalmente, cabe destacar que, si estuviéramos trabajando con puntos de 3 coordenadas, la fórmula de la distancia entre dos puntos en el espacio (en R3) sería la misma pero añadiendo la coordenada Z:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}

Ejemplo de cómo calcular la distancia entre dos puntos

Una vez hemos visto la definición de la fórmula de la distancia entre dos puntos, veamos ahora cómo determinar dicha distancia mediante un ejemplo:

  • Halla la distancia entre los siguientes dos puntos:

A(-1,7) \qquad \qquad B(3,4)

Para hallar la distancia entre los dos puntos geométricamente simplemente debemos aplicar la fórmula:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}

Ahora sustituimos las coordenadas de los puntos en la fórmula:

d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}

Y hacemos los cálculos:

\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}

De modo que la distancia entre los dos puntos es igual a 5 unidades.

Evidentemente, el valor de la distancia siempre nos tiene que dar de signo positivo, porque las distancias siempre son positivas. De lo contrario, significa que nos hemos equivocado en algún paso.

Ejercicios resueltos de la distancia entre dos puntos

Ejercicio 1

Calcula la distancia entre los siguientes dos puntos:

A(4,2) \qquad \qquad B(1,5)

Para hallar la distancia geométrica entre los dos puntos simplemente debemos utilizar la fórmula:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}

Ahora sustituimos las coordenadas de los puntos en la fórmula:

d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}

Y hacemos los cálculos:

\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}

 

Ejercicio 2

Averigua la distancia entre los siguientes dos puntos:

A(8,6) \qquad \qquad B(-4,1)

Para hallar la distancia matemática entre los dos puntos debemos usar la fórmula correspondiente:

d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}

Ahora sustituimos las coordenadas de los puntos en la fórmula:

d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}

Y hacemos los cálculos:

\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}

 

Ejercicio 3

Calcula el perímetro del triángulo formado por los puntos A, B y C que está representado gráficamente a continuación:

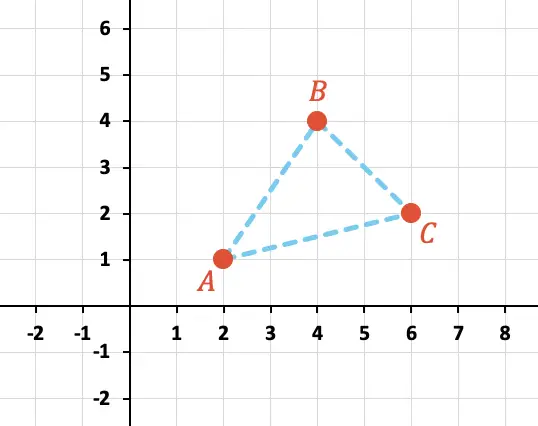
ejercicio resuelto de la distancia entre dos puntos

En primer lugar, debemos identificar las coordenadas X e Y de cada punto en el gráfico:

A(2,1)

B(4,4)

C(6,2)

Y ahora tenemos que calcular la distancia entre todos los puntos con la fórmula:

d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61

d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12

d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83

De manera que el perímetro del triángulo será la suma de la longitud de los 3 lados:

P=3,61+4,12+2,83= \bm{10,56}

 

Ejercicio 4

Comprueba si el triángulo que tiene como vértices los puntos A, B y C se trata de un triángulo isósceles. Siendo los tres puntos:

A(-4,5) \qquad B(7,-5) \qquad C(10,0)

Para que el triángulo sea isósceles, dos de sus lados deben ser iguales. Por lo tanto, tenemos que hallar la longitud de cada uno de sus lados, que corresponden a las distancias entre sus vértices.

Así que calculamos la distancia entre los vértices del triángulo:

d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}

d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}

d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}

De modo que el triángulo tiene 2 lados idénticos y el tercer lado mide diferente a los otros dos, por tanto, efectivamente se trata de un triángulo isósceles.

 

Ejercicio 5

Encuentra un punto sobre el eje Y que es equidistante de los siguientes dos puntos:

A(5,-3) \qquad \qquad B(-2,4)

Primero de todo, si el punto está situado en el eje de las ordenadas (eje OY) significa que la coordenada X del punto es nula:

P(0,y)

En segundo lugar, si el punto equidista de los puntos A y B, implica que se cumple la siguiente ecuación:

d(P,A)= d(P,B)

De forma que, utilizando la fórmula de la distancia entre dos puntos, podemos hallar el valor de la variable y a partir de la ecuación anterior:

\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}

Como los dos lados de la ecuación tienen una raíz, las podemos simplificar:

5^2+(-3-y)^2=(-2)^2+(4-y)^2

Resolvemos las potencias y las igualdades notables (o productos notables):

25+9+y^2+6y=4+16+y^2-8y

Y operamos hasta encontrar el valor de la incógnita y:

y^2+6y-y^2+8y=4+16-25-9

14y=-14

y=\cfrac{-14}{14}

y=-1

En definitiva, el punto que nos pedía el enunciado del problema es:

\bm{P(0,-1)}

 

Si te ha sido útil este artículo, seguramente también te interese practicar con ejercicios de la distancia entre un punto y una recta. En la página enlazada no solo encontrarás ejercicios resueltos paso a paso, sino también la explicación al detalle de cómo se calcula la distancia entre puntos y rectas, ejemplos y la aplicación que tiene la fórmula de la distancia entre un punto y una recta para determinar otro tipo de distancia.

55 comentarios en “Fórmula de la distancia entre dos puntos (geometría)”

    1. Geometría Analítica

      Hola Susana,

      Para calcular la distancia entre los dos puntos tienes que restar las coordenadas de los puntos, elevar los resultados al cuadrado, sumarlos y, finalmente, hacer la raíz cuadrada:

      \begin{aligned}d(A,B)&=\sqrt{\bigl(3-(-5)\bigr)^2+\bigl(5-(-1)\bigr)^2}\\ &= \sqrt{8^2+6^2}\\ &= \sqrt{64+36}\\ & = \sqrt{100}\\ &= 10 \end{aligned}

    1. Geometría Analítica

      Hola Susana de nuevo, para averiguar la distancia entre los dos puntos debes aplicar la fórmula explicada en el post:

      \begin{aligned}d(C,D)&= \sqrt{\bigl(-7-(-5)\bigr)^2+(4-5)^2}\\ &=\sqrt{(-2)^2+1^2}\\ & = \sqrt{4+1}\\ & =\sqrt{5} \end{aligned}

    2. Sarai

      HALLAR LA DISTANCIA ENTRE LOS PUNTOS, UNIENDO LOS PUNTOS DADOS. GRAFICAR
      H(17/6;√5,3) K(5,1;3²).
      Me explicas por favor para realizar los demás, gracias

    3. Geometría Analítica

      Hola Sarai,

      El enunciado se refiere a que calcules la distancia entre los pares de puntos que te da. Para ello, debes aplicar la fórmula explicada en este artículo, fíjate en el siguiente ejemplo:

      \displaystyle \begin{aligned}d(H,K)&=\sqrt{\left(5,1-\frac{17}{6}\right)^2 +(3^2-\sqrt{5,3})^2}\\[2ex] &= \sqrt{2,267^2+6,70^2}\\[2ex] &= \sqrt{50}\end{aligned}

    5. Geometría Analítica

      Hola Caridad,

      Para hallar la distancia entre estos dos puntos simplemente tienes que emplear la fórmula correspondiente:

      d(A,B)=\sqrt{(4-4)^2+(-6-5)^2}=\sqrt{0+121}=11

  4. Jonathan Ayala

    Buenas! Te aviso que en la imagen, donde está recuadrada la “fórmula” para calcular distancia entre dos puntos, se encuentra con un error, ya que en lugar de plantear la suma de los catetos al cuadrado, aparece una resta.
    Saluda, profesor en matemática Jonathan Ayala. Durazno, Uruguay.

    Responder
    1. Geometría Analítica

      ¡Muchas gracias Jonathan! Tenías toda la razón, en todo el artículo la fórmula estaba bien pero en la imagen el signo estaba cambiado, ya está corregido. ¡Gracias por reportar el error! ¡Espero que te vaya genial con tus clases!

    3. Geometría Analítica

      Hola Eduin.

      El cálculo de la distancia geométrica entre los dos puntos se hace con la siguiente fórmula:

      \begin{aligned}d(A,N) &= \sqrt{(3-(-2))^2+(1-4)^2\\[2ex] & = \sqrt{5^2+(-3)^2 \\[2ex]& =\sqrt{34}\end{aligned}

    4. Andres

      Hola. Buen día
      Quisiera saber si me puedes ayudar a resolver este ejercicio
      Hallar la distancia entre los puntos:
      P (3,1,5 ) Q (0,4,8)

      Gracias

    5. Geometría Analítica

      Hola Andres, en este caso los dos puntos están expresados con tres coordenadas, por lo que debemos utilizar la misma fórmula de la distancia entre dos puntos pero aplicada en el espacio, que es equivalente a la fórmula en el plano cartesiano pero simplemente debemos sumar el cuadrado de la diferencia entre las componentes del eje Z dentro de la raíz:

      \begin{aligned}d(P,Q)&=\sqrt{(0-3)^2+(4-1)^2+(8-5)^2}\\[2ex]&=\sqrt{3^2+3^2+3^2}\\[2ex]&=\sqrt{27}\end{aligned}

    6. Darian

      Podrias ayudarme con éste ejercicio:( Uno de los extremos de un segmento de longitud igual a 3, es el punto (3, 2, 1). Si las coordenadas X y Y del otro extremo son 5 y 3 respectivamente. Hallar los posibles valores de la coordenada Z.

    7. Geometría Analítica

      Hola Darian,

      Utilizando la fórmula de la distancia entre dos puntos (en el espacio) puedes plantear la siguiente ecuación:

      3=\sqrt{(3-5)^2+(2-3)^2+(1-Z)^2}

      Y resolviendo esta ecuación se obtienen los dos posibles valores de la coordenada Z:

      Z=-1 \qquad Z=3

    1. Geometría Analítica

      Hola Sol,

      Entiendo que te refieres a hallar la distancia entre esos dos puntos. Para hacerlo debes emplear la siguiente fórmula:

      \begin{aligned}d(C,D) &= \sqrt{(7-5)^2+(-1-(-1))^2\\[2ex] & = \sqrt{2^2+0^2 \\[2ex]& =2\end{aligned}

      Si te referías a encontrar la ecuación de la recta que pasa por estos dos puntos, puedes consultar cómo se hace en nuestro post de ecuaciones de la recta.

    1. Geometría Analítica

      Hola Estefani,

      La distancia entre dos puntos en el plano cartesiano se calcula de la siguiente manera:

      d(P_1,P_2)=\sqrt{(7-2)^2+(3-3)^2}=\sqrt{5^2}=5

  7. Angel

    Si dos puntos son de la forma (3,y1) y (3,y2), deduzca una formula para la distancia entre estos puntos en que no aparezcan radicales. Generalice.

    Responder
    1. Geometría Analítica

      Hola Angel, si te fijas las coordenadas X de los dos puntos son iguales, por lo que al aplicar la fórmula de la distancia entre estos dos puntos se simplifica la expresión:

      d(A,B)=\sqrt{(3-3)^2+(y_2-y_1)^2}=\sqrt{(y_2-y_1)^2}=y_2-y_1

    1. Geometría Analítica

      Hola Raul,

      En el plano cartesiano, la distancia entre dos puntos se saca con la siguiente fórmula:

      d(C,D)=\sqrt{(5-(-2))^2+(4-(-3))^2}=\sqrt{7^2+7^2}=\sqrt{98}

    1. Geometría Analítica

      Hola Giselle,

      La distancia entre estos dos puntos se calcula de la siguiente manera:

      d(M,N)=\sqrt{(8-3)^2+\bigl((-2)-(-6)\bigr)^2}=\sqrt{5^2+4^2}=\sqrt{41}

    1. Geometría Analítica

      Hola Jhon,

      Para referenciar esta página lo único importante es que pongas un enlace al artículo que has utilizado para tu trabajo.

      No tiene fecha de publicación porque el contenido se va actualizando, por eso se suele recomendar poner la fecha en que visitaste la página cuando se cita un artículo de internet.

      ¡Muchas gracias por citarnos!

    2. Nahuel

      Buenas noches, una consulta. ¿Con esto se puede investigar analíticamente la pertenencia de tales puntos a la recta? Por ejemplo, del punto Q(-5,-4) a una recta AB [A(-1,4) B(2,10]. Muchas gracias de antemano!

    3. Geometría Analítica

      Hola Nahuel,

      Sabiendo cuál es la distancia entre dos puntos no puedes saber si un punto pertenece a una recta. De hecho, dos puntos de una misma recta pueden estar muy juntos o muy separados.

      Para averiguar si un punto forma parte de una recta primero debes encontrar la ecuación de dicha recta, y entonces sustituyes las coordenadas del punto en la ecuación. Si el punto cumple con la ecuación significa que pertenece a esa recta, de lo contrario, el punto no se incluye en dicha recta.

    1. Geometría Analítica

      Hola Aurelio,

      El cálculo de la distancia entre estos dos puntos se hace usando la siguiente fórmula:

      \sqrt{\bigl(-4-(-1)\bigr)^2+(-6-5)^2}=\sqrt{(-3)^2+(-11)^2}=\sqrt{9+121}=\sqrt{130}

  13. Rocio

    En un plano de La Habana realizado con una E1cm=750m se aprecia que entre Ciudad Escolar Libertad y el teatro García Lorca media una distancia de 11,5cm. ¿Qué distancia real existe entre estos dos puntos?

    Responder
    1. Geometría Analítica

      Hola Rocío,

      La escala con la que está dibujado el mapa es de 1 cm= 750 m, por lo tanto, para calcular la distancia entre estos dos puntos se debe multiplicar la distancia medida por la escala del plano mediante un factor de conversión:

      11,5 \ cm \cdot \cfrac{750 \ m}{1 \ cm} =8625 \ m

    1. Geometría Analítica

      Hola Ritha, para determinar la distancia simplemente debes usar la fórmula explicada en el post:

      d(A,B)=\sqrt{\bigl(-1-(-4)\bigr)^2+(3-7)^2}=\sqrt{3^2+(-4)^2}=\sqrt{25}=5

    1. Geometría Analítica

      Hola Naomy,

      Para resolver este problema debes encontrar la distancia entre cada punto y el punto P utilizando la fórmula de la distancia geométrica entre dos puntos. De manera que el punto más cercano será aquel cuya distancia sea menor.

    1. Geometría Analítica

      Hola Gaby,

      Aunque en la coordenada de un punto haya una raíz, la distancia entre dos puntos se calcula de la misma manera, debes utilizar la fórmula explicada en el post:
      d=\sqrt{\bigl(1-(-1)\bigr)^2+\bigl(\sqrt{3}-1\bigr)^2}=2,13

    1. Geometría Analítica

      Buenas Javier,

      La distancia geométrica entre los dos puntos es:

      \sqrt{\bigl(3-(-5)\bigr)^2+(2-6)^2}=\sqrt{8^2+(-4)^2}=\sqrt{64+16}=\sqrt{80}

    1. Geometría Analítica

      Hola Jimena,

      Para hacer el cálculo de la distancia debes utilizar la fórmula explicada:

      d(A,B)=\sqrt{(-6-5)^2+(-2-3)^2)}=\sqrt{121+25}=\sqrt{146}

    1. Geometría Analítica

      Hola Danyely, en este caso muchas parejas de puntos cumplen con los requisitos del problema. Por ejemplo, los puntos (0,0) y (4,0).

    1. Geometría Analítica

      La distancia entre estos dos puntos se puede determinar a simple vista, ya que la coordenada X es la misma para ambos puntos. Entonces, como la diferencia entre las coordenadas Y es de 2 unidades, la distancia entre los dos puntos es igual a 2.

    1. Geometría Analítica

      Hola Ruben,

      Si un punto es equidistante significa que está a la misma distancia. Por lo tanto, se debe cumplir la siguiente ecuación:

      d(P,A)=d(P,B)

      Aplicando la fórmula de la distancia entre dos puntos obtenemos:

      \sqrt{\bigl(1-m\bigr)^2+\bigl(2-(m+3)\bigr)^2}=\sqrt{\bigl(-3-m\bigr)^2+\bigl(5-(m+3)\bigr)^2}

      Y resolviendo la ecuación radical llegamos a la solución del problema:

      m=-5,5

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio