▷ ¿Cómo calcular el Punto Medio de un segmento? (fórmula)

En esta página se explica el significado del punto medio de un segmento. Además, encontrarás cómo hallar el punto medio de un segmento a través de su fórmula. Incluso podrás ver ejemplos, ejercicios y problemas resueltos de puntos medios de segmentos.

Índice

¿Qué es el punto medio de un segmento?

En matemáticas, el punto medio de un segmento es aquel punto que se encuentra a la misma distancia de los extremos de un segmento. Por lo tanto, el punto medio divide el segmento en dos partes iguales.

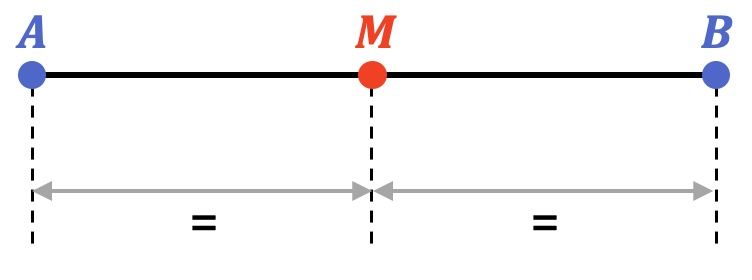
definicion de punto medio de un segmento

Además, el punto medio está justo en el centro del segmento, por lo que pertenece a la mediatriz del segmento.

Por otro lado, el punto medio de un segmento también es un punto equidistante de dos elementos geométricos: los dos extremos del segmento.

¿Cómo se calcula el punto medio de un segmento?

Dadas las coordenadas cartesianas de los puntos extremos de un segmento:

$A(x_1,y_1) \qquad B(x_2,y_2)$

Las coordenadas del punto medio de dicho segmento corresponde a la semisuma de las coordenadas de los puntos extremos:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Esta es la fórmula del punto medio de un segmento en el plano cartesiano (en R2). Pero evidentemente la fórmula también es aplicable al espacio cartesiano (en R3), solo tenemos que añadir la semisuma de la coordenada Z:

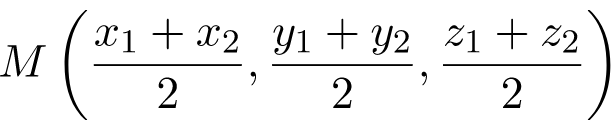
Veamos un ejemplo de cómo calcular las coordenadas del punto medio de un segmento:

Determina el punto medio del segmento que forman los siguientes puntos:

$A(2,5) \qquad B(4,-1)$

Para hallar el punto medio del segmento, lo único que debemos hacer es aplicar su fórmula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Ejercicios resueltos de punto medio de un segmento

Ejercicio 1

¿Cuál es el punto medio del segmento cuyos extremos son los siguientes dos puntos?

$A(3,-2) \qquad B(5,8)$

Ver solución

Para averiguar el punto medio del segmento debemos aplicar directamente la fórmula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Ejercicio 2

Halla las coordenadas del extremo final del segmento que empieza en el punto A y cuyo punto medio es M.

$A(4,-1) \qquad M(-2,1)$

Ver solución

En este caso sabemos las coordenadas del punto inicial y del punto medio del segmento. Por lo tanto, sustituimos las coordenadas que sabemos en la fórmula del punto medio de un segmento:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

Y ahora despejamos las coordenadas del punto final del segmento a partir de la ecuación anterior:

Coordenada X

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Coordenada Y

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

De modo que las coordenadas del extremo final del segmento son:

$\bm{B(-8,3)}$

Ejercicio 3

Dado el siguiente paralelogramo:

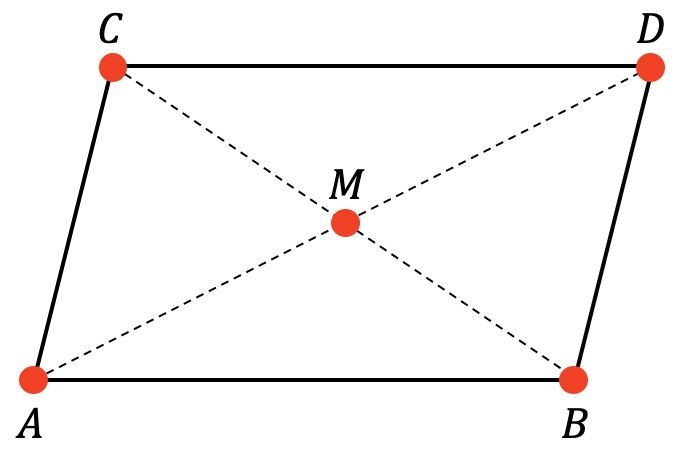
Sabemos que M es el centro del paralelogramo y las coordenadas de los puntos A, B y C son:

$A(1,1) \quad B(5,1) \quad C(7,3)$

A partir de esta información y utilizando la fórmula del punto medio, calcula las coordenadas del punto D.

Ver solución

Para hallar las coordenadas del punto D mediante la fórmula del punto medio de un segmento, debemos calcular primero las coordenadas del punto M y luego las del punto D.

El punto M es el punto medio del segmento BC, así que sus coordenadas son:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

Y una vez ya conocemos el punto M, podemos encontrar el punto D. El punto M también es el punto medio del segmento AD, por tanto:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

Coordenada X del punto D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Coordenada Y del punto D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

De manera que las coordenadas del punto D son:

$\bm{D(11,3}$

Ejercicio 4

Calcula la ecuación continua de la recta que es perpendicular al segmento PQ en su punto medio. Siendo los puntos $P(1,4)$ y $Q(5,-2).$

Ver solución

Para determinar la ecuación de una recta necesitamos su vector director y un punto que forme parte de la recta.

En este caso, el vector director de la recta será perpendicular al vector $\vv{PQ}.$ Por lo tanto, calculamos el vector $\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

Y podemos hallar un vector perpendicular a otro cambiando las componentes del vector entre sí y luego cambiando de signo una componente, por tanto:

$\vv{PQ}_\perp =(6,4)$

Ahora ya tenemos el vector director de la recta, así que solo nos falta un punto que pertenezca a la recta. En este caso, el enunciado nos dice que la recta pasa por el punto medio del segmento, así que calculamos el punto medio mediante la fórmula:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Finalmente, construimos la ecuación continua de la recta a partir del punto y el vector calculados:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

6 comentarios en “Fórmula del punto medio de un segmento”

Santiago Alonso
18/08/2021 a las 04:50

Es muy buena la información

Responder
1. Geometría Analítica
  21/08/2021 a las 18:59
  
  ¡Me alegro Santiago! ¡Gracias por compartir tu opinión! 🙂
Danni
08/01/2022 a las 00:20

Si el punto medio de un segmento de recta es pm(1-3)y un extremo del segmento es p1(7-1)¿cuál es la cordenada del otro extremo?

Responder
1. Geometría Analítica
  09/01/2022 a las 20:31
  
  Hola Danni,
  
  Para determinar las coordenadas del otro extremo simplemente debes usar la fórmula del punto medio y resolver las dos ecuaciones resultantes.
  
  Primero calculamos la coordenada X del punto:
  
  $\cfrac{7+x_2}{2}=1$
  
  $7+x_2=1\cdot 2$
  
  $7+x_2=2$
  
  $x_2=-5$
  
  Y luego hallamos la coordenada Y del punto:
  
  $\cfrac{-1+y_2}{2}=-3$
  
  $-1+y_2=-3\cdot 2$
  
  $-1+y_2=-6$
  
  $y_2=-5$
  
  En definitiva, las coordenadas del otro extremo son:
  
  [latex]P_2(-5,-5)
Mauricio
15/02/2022 a las 01:52

Hola, y si tengo una variable en una coordenada?

es decir:

¿Puedo encontrar el punto medio de una recta que pasa por P1(-4,5) y P2(x,2)?

Responder
1. Geometría Analítica
  25/02/2022 a las 20:54
  
  Hola Mauricio,
  
  Primero de todo, no se puede determinar el punto medio de una recta, ya que son infinitas.
  
  Si te refieres al cálculo del punto medio entre estos dos puntos, tendrías que saber el valor de la coordenada. De lo contrario, el resultado del punto medio estará en función de dicha incógnita.

¿Qué es el punto medio de un segmento?

¿Cómo se calcula el punto medio de un segmento?

Ejercicios resueltos de punto medio de un segmento

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

6 comentarios en “Fórmula del punto medio de un segmento”

Deja un comentario Cancelar respuesta