Punto simétrico respecto a otro punto, a una recta y a un plano

Aquí encontrarás cómo se calcula el punto simétrico respecto a otro punto, respecto a una recta y respecto a un plano. Además, podrás ver ejemplos y ejercicios resueltos paso a paso.

Índice

Punto simétrico respecto a otro punto

Antes de ver cómo se calcula el punto simétrico, repasemos qué es exactamente un punto simétrico respecto a otro punto:

El punto A’ es el punto simétrico del punto A respecto a otro punto M si el punto A’ está situado simétricamente a la misma distancia del punto M que la distancia que hay entre los puntos A y M. Por tanto, M es el punto medio del segmento formado por los puntos A y A’.

$d(A,M) = d(A',M )$

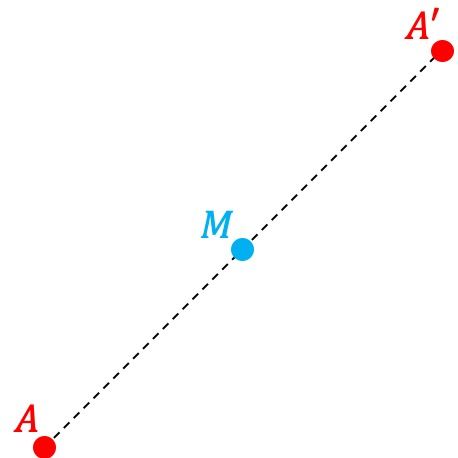
Por otro lado, el punto M también se dice que es el centro de simetría.

Entonces, para calcular las coordenadas del punto simétrico, utilizaremos la fórmula del punto medio de un segmento:

$\cfrac{A+A'}{2}=M$

De esta ecuación despejamos el punto incógnita A’ y obtenemos la fórmula del punto simétrico respecto a otro punto:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

Ejemplo de cómo hallar el punto simétrico respecto a otro punto

A modo de ejemplo, vamos a calcular el punto simétrico del punto A respecto al punto M. Siendo los dos puntos:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

Para determinar el punto simétrico entre esos dos puntos, aplicamos la fórmula del punto simétrico respecto a otro:

$A' = 2M - A$

Ahora sustituimos los puntos en la fórmula:

$A' = 2(-1,4,2) -(1,3,0)$

Y operamos:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

Punto simétrico respecto a una recta

Acabamos de ver el concepto de punto simétrico respecto a otro punto. Pues el punto simétrico de un punto respecto a una recta es muy similar:

El punto A’ es el punto simétrico del punto A respecto a una recta si ambos puntos A’ y A se encuentran en una misma línea perpendicular a la recta y, además, la distancia entre el punto A’ y la recta es igual a la distancia entre el punto A y la recta.

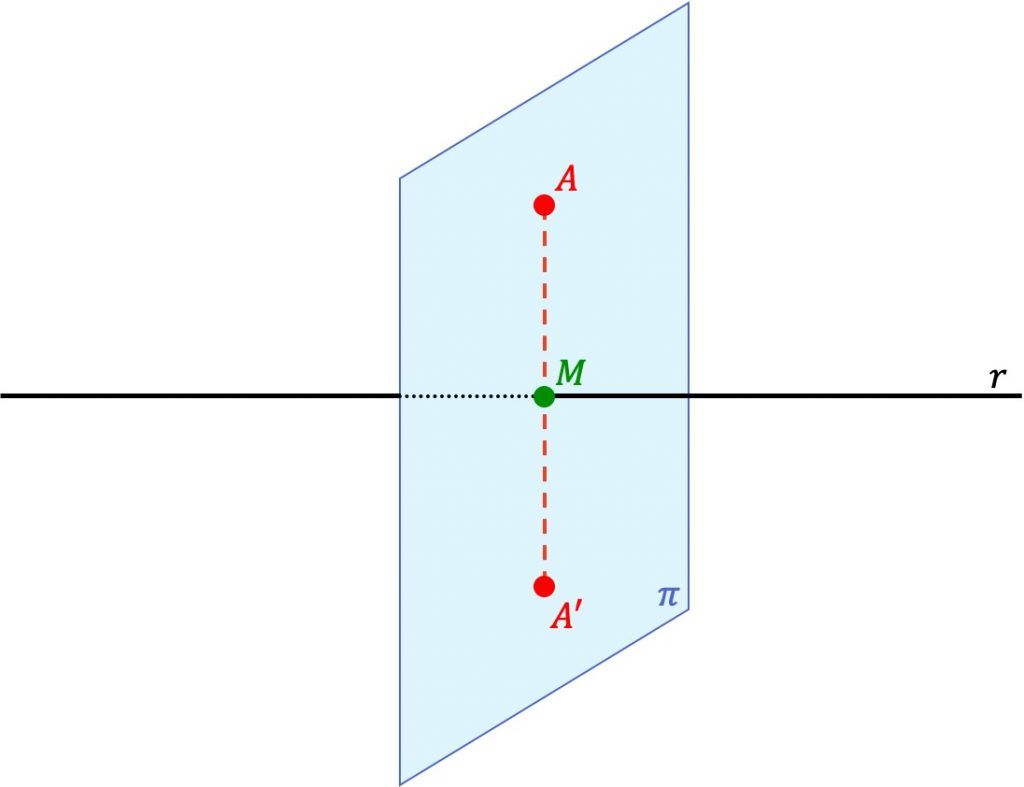
punto simetrico de un punto respecto a una recta

$d(A,r)= d(A',r)$

De modo que la recta r también es un eje de simetría entre los puntos.

Así pues, para determinar el punto simétrico del punto A respecto a la recta r, debemos seguir el siguiente procedimiento:

Hallamos el plano perpendicular a la recta r que pasa por el punto A (plano π de la representación gráfica anterior). Para ello debemos utilizar el vector director de la recta, que será el vector normal del plano.
Calculamos el punto de corte entre el plano hallado y la recta (punto M de la imagen anterior).
Usamos la fórmula del punto simétrico respecto a un punto (vista en el apartado de arriba) para encontrar el punto simétrico del punto A respecto del punto M. El resultado es el punto simétrico que estábamos buscando.

Ejemplo de cómo calcular el punto simétrico respecto a una recta

Una vez ya sabemos cómo se calcula el punto simétrico de otro punto respecto a una recta, vamos a ver un ejercicio resuelto como ejemplo:

Halla el punto simétrico del punto A respecto de la recta r. Siendo dicho punto y recta:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

En primer lugar, tenemos que calcular el plano perpendicular a la recta r que pasa por el punto A. El vector normal a ese plano será el vector director de la recta, cuyas componentes son los términos de delante del parámetro $t$ porque está expresada en forma de ecuaciones paramétricas:

$\vv{n}=(1,4,-3)$

Y los coeficientes A, B y C de la ecuación de un plano coinciden con las coordenadas de su vector normal, por lo tanto:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

El punto A debe pertenecer a este plano, por lo que ahora podemos sustituir el punto A en la ecuación del plano para encontrar el coeficiente D:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

De manera que la ecuación del plano perpendicular a la recta r y que pasa por el punto A es:

$\pi : \ x+4y-3z-7=0$

Una vez conocemos la ecuación del plano, tenemos que calcular el punto en el que se cortan el plano y la recta. Para ello, sustituimos las coordenadas de la recta en la ecuación del plano y resolvemos la ecuación resultante:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

Ahora sustituimos el valor de $t$ obtenido en la ecuación de la recta:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

Así que el punto de intersección entre la recta r y el plano perpendicular a ella es:

$M(0,1,-1)$

Finalmente, solo nos queda encontrar el punto simétrico del punto A respecto al punto M, para ello, podemos usar la fórmula vista al principio de esta página:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

Punto simétrico respecto a un plano

Antes de ver el método para determinar el punto simétrico de otro punto respecto a un plano, veamos cuál es su definición:

El punto A’ es el punto simétrico del punto A respecto a un plano si ambos puntos A’ y A se encuentran en una misma línea perpendicular al plano y, además, la distancia entre el punto A’ y el plano es equivalente a la distancia entre el punto A y el plano.

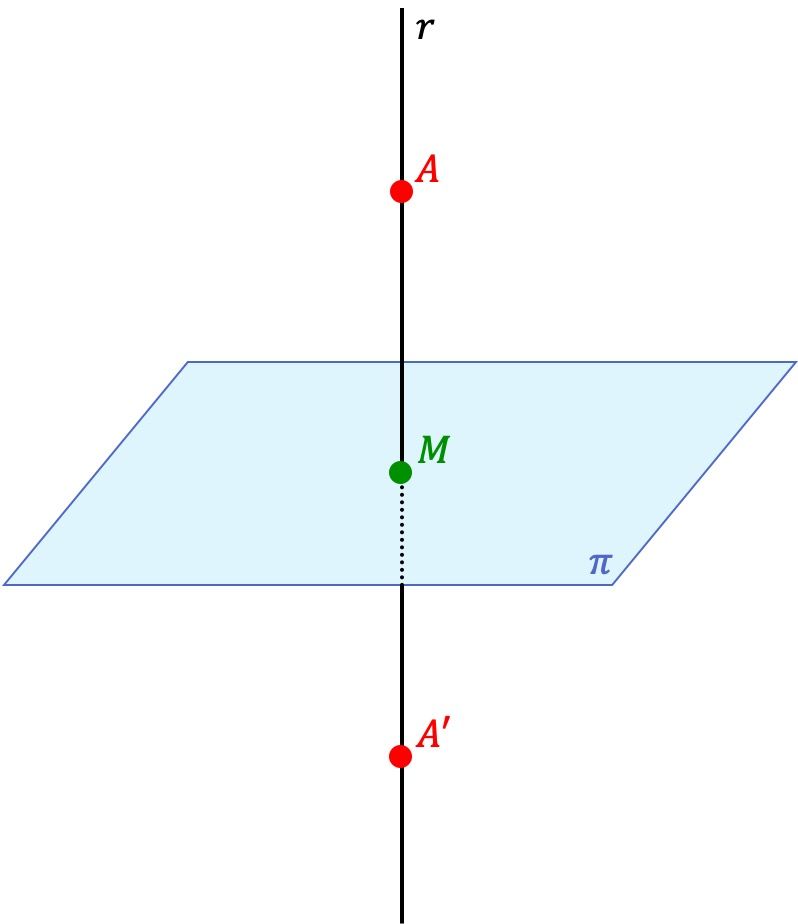
punto simetrico de otro punto respecto a un plano

$d(A,\pi)= d(A',\pi)$

De modo que el plano también es un plano de simetría entre los dos puntos.

Así pues, para averiguar las coordenadas cartesianas del punto simétrico del punto A respecto al plano π, debemos seguir los siguientes pasos:

Hallamos la ecuación de la recta perpendicular al plano que pasa por el punto A. Para ello usaremos el vector normal al plano como vector director de la recta.
Calculamos el punto de intersección entre el plano y la recta hallada (punto M de la imagen anterior).
Usamos la fórmula del punto simétrico respecto a un punto (vista en el apartado del principio) para encontrar el punto simétrico del punto A respecto del punto M. El resultado es el punto simétrico que estábamos buscando.

Ejemplo de cómo determinar el punto simétrico respecto a un plano

A continuación puedes ver un problema resuelto sobre el punto simétrico de otro punto respecto a un plano:

Determina el punto simétrico de A respecto del plano π. Siendo dichos punto y plano:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

Lo primero que debemos hacer es encontrar la ecuación de la recta perpendicular al plano y que pasa por el punto A. Para ello, podemos utilizar como vector director de la recta el vector normal al plano, cuyas componentes X, Y, Z son los coeficientes de los términos A, B y C respectivamente de la ecuación del plano:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$

Ahora podemos construir las ecuaciones paramétricas de la recta ortogonal al plano con el vector director encontrado y uno de sus puntos (el punto A):

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}$

Una vez conocemos la recta perpendicular, calculamos el punto donde se cruzan el plano y la recta sustituyendo las coordenadas de la recta en la ecuación del plano:

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0$

$2(3+2t)+(-4+t)-(2-t)-6=0$

$6+4t-4+t-2+t-6=0$

$6t-6=0$

$6t=6$

$t=\cfrac{6}{6}$

$t=1$

Ahora sustituimos el valor de $t$ obtenido en la ecuación de la recta:

$\displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}$

Así que el punto de corte entre el plano y la recta perpendicular es:

$M(5,-3,1)$

Por último, solamente nos falta encontrar el punto simétrico del punto A respecto al punto M. Y, para ello, podemos usar la fórmula vista al principio de esta página:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}$

3 comentarios en “Punto simétrico respecto a otro punto, a una recta y a un plano”

Lidia Nicolai
13/10/2021 a las 00:51

Está buenísima la explicación. Muchas gracias!!!

Responder
1. Geometría Analítica
  13/10/2021 a las 12:24
  
  ¡Gracias a ti por el comentario Lidia! 🙂
carlota
12/05/2023 a las 07:29

Explicación excelente, sobre todo por los ejemplos, gracias

Responder