En esta página encontrarás qué son los planos perpendiculares, cómo determinar si dos planos son perpendiculares, cómo calcular un plano perpendicular, ejemplos y ejercicios resueltos de planos perpendiculares,…
Índice
¿Qué son dos planos perpendiculares?
En geometría analítica, dos planos son perpendiculares cuando se cortan formando un ángulo recto (de 90º).
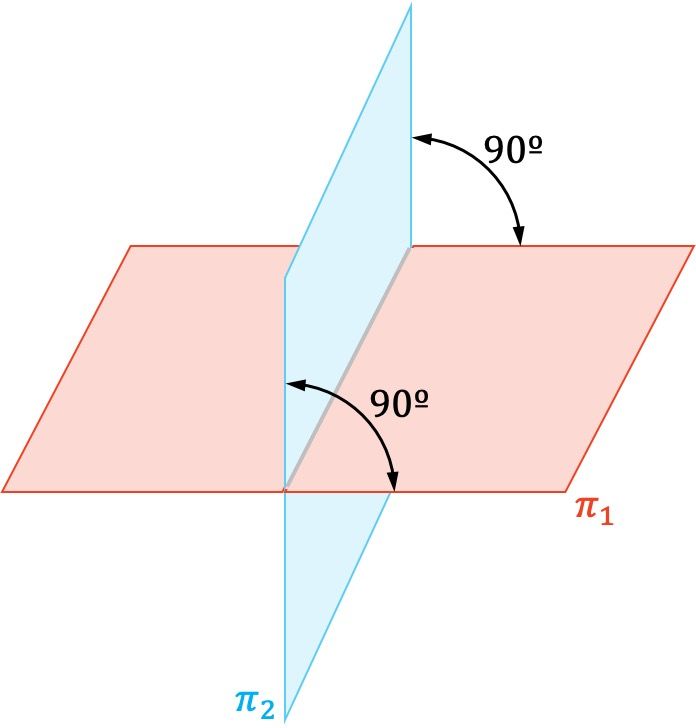
Además, los vectores normales de dos planos perpendiculares también son ortogonales entre sí.
Evidentemente, la distancia entre dos planos perpendiculares siempre es nula, porque se intersecan en una recta. Aunque parece muy simple, el concepto de distancia entre dos planos es muy importante, así que te recomendamos que visites el enlace si tienes alguna duda al respecto.
Por otro lado, dos planos posicionados perpendicularmente no es la única posición relativa posible entre los planos, ya que dos planos en el espacio (en R3) también pueden ser secantes, paralelos o coincidentes.
¿Cómo saber si un plano es perpendicular a otro?
Una vez vista la definición de los planos perpendiculares, veamos cómo saber si dos planos son perpendiculares o no:
Dos planos son perpendiculares cuando sus vectores normales son perpendiculares. Por lo tanto, para determinar si dos planos son perpendiculares entre sí se debe calcular el ángulo que forman sus vectores normales, y si estos forman un ángulo de 90º significa que los planos son perpendiculares.
De manera que para hallar la perpendicularidad de dos planos debes saber cómo calcular el ángulo entre dos vectores. Si no recuerdas cómo se hace puedes consultar el enlace, donde encontrarás nuestra explicación junto con la fórmula necesaria para determinar el ángulo entre dos vectores. Además, podrás ver ejemplos y practicar con ejercicios resueltos.
Pero en resumen, dos vectores son perpendiculares cuando su producto escalar es igual a cero. Por lo que dos planos serán perpendiculares cuando el producto escalar de sus vectores normales asociados sea equivalente a 0.
Ejemplo de dos planos perpendiculares
Por ejemplo, vamos a comprobar si los siguientes dos planos son perpendiculares:
Las coordenadas X, Y, Z del vector normal a un plano coincide con los coeficientes A, B, C de su ecuación general (o implícita). Por lo tanto, el vector normal a cada plano es:
Y ahora verificamos si se trata de dos planos perpendiculares calculando el producto escalar entre sus vectores normales:
![\begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-89fadde3eca8f96ff97ddd7bb813af6a_l3.svg "Rendered by QuickLaTeX.com")
El producto escalar entre los dos vectores normales es igual a 0, por lo tanto, los dos planos son perpendiculares entre sí.
Calcular un plano perpendicular a una recta en un punto
Un problema típico de planos y rectas es hallar la ecuación de un plano que es perpendicular a una recta en un determinado punto. Así pues, a continuación vamos a ver cómo se resuelve mediante un ejemplo:
- Calcula la ecuación del plano que es perpendicular a la recta
en el punto 
siendo dicha recta y punto:
![\displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-7eea89d639100284cde51d5719fc77f9_l3.svg "Rendered by QuickLaTeX.com")
En primer lugar, debemos encontrar el vector normal al plano en cuestión. Y como la recta es perpendicular al plano, su vector normal coincidirá con el vector director de la recta.
En este caso, la recta está en forma de ecuaciones paramétricas, por lo que las componentes de su vector director son los términos de delante del parámetro 
De manera que el vector normal al plano será el mismo que el vector director de la recta:
Y, por tanto, la ecuación implícita (o general) del plano será de la siguiente forma:
Así que solo nos queda determinar el valor del coeficiente D. Para ello, sustituimos las coordenadas del punto que el enunciado nos dice que pertenece al plano en su ecuación:
En definitiva, la ecuación cartesiana del plano es:
Por otro lado, si quieres practicar con más ejercicios sobre la perpendicularidad entre objetos geométricos, puedes visitar nuestra página de las rectas perpendiculares. Allí encontrarás todo lo que debes saber sobre las rectas perpendiculares: cuándo dos rectas son perpendiculares, cómo calcular una recta perpendicular a otra, ejemplos, ejercicios resueltos y mucho más.
Propiedades de los planos perpendiculares
Todas los planos perpendiculares tienen las siguientes características:
- Relación simétrica: si un plano es perpendicular a otro plano, ese plano también es perpendicular al primer plano. Esta propiedad también la tienen los planos paralelos.
- Propiedad irreflexiva: obviamente, ningún plano puede ser perpendicular a sí mismo.
- Teorema: en un espacio tridimensional (3D), cualquier par de planos que son perpendiculares a un tercer plano deben ser necesariamente paralelos. O dicho de otra forma, si un plano es perpendicular a otro plano y este plano es a la vez perpendicular a un tercer plano, el primer y el último plano son paralelos entre sí.