▷ ¿Cómo se calcula la distancia entre dos planos? ✅ (fórmula y ejemplos)

En esta página encontrarás cómo hallar la distancia entre dos planos. En particular, verás los dos métodos que existen y cuándo es mejor utilizar uno u otro. Además, tienes ejemplos y ejercicios resueltos de la distancia entre dos planos para poderlo entender del todo.

Índice

¿Cómo se calcula la distancia entre dos planos?

La distancia entre dos planos en el espacio depende de la posición relativa entre esos dos planos:

Si los dos planos son secantes o coincidentes, la distancia entre ellos es igual a cero porque se cortan en algún punto.
Si los dos planos son paralelos, se calcula la distancia entre los dos planos tomando un punto de cualquiera de los dos planos y calculando la distancia entre dicho punto y el otro plano.

Recuerda que los planos perpendiculares son un tipo de planos secantes, por lo que la distancia entre dos planos perpendiculares también es nula.

De manera que para poder calcular la distancia entre dos planos primero se tiene que determinar cuál es la posición relativa entre ellos y, por lo tanto, es imprescindible que sepas cómo hallar la posición relativa de dos planos. Si no tienes del todo claro cómo se hace te recomendamos que le eches un vistazo al enlace, donde encontrarás toda una explicación bien detallada junto con ejemplos y ejercicios resueltos.

Cómo calcular la distancia entre dos planos paralelos

Dos planos paralelos siempre están a la misma distancia entre sí, por lo tanto, para encontrar la distancia entre dos planos paralelos podemos coger un punto de cualquiera de los dos planos y calcular la distancia que hay desde ese punto hasta el otro plano.

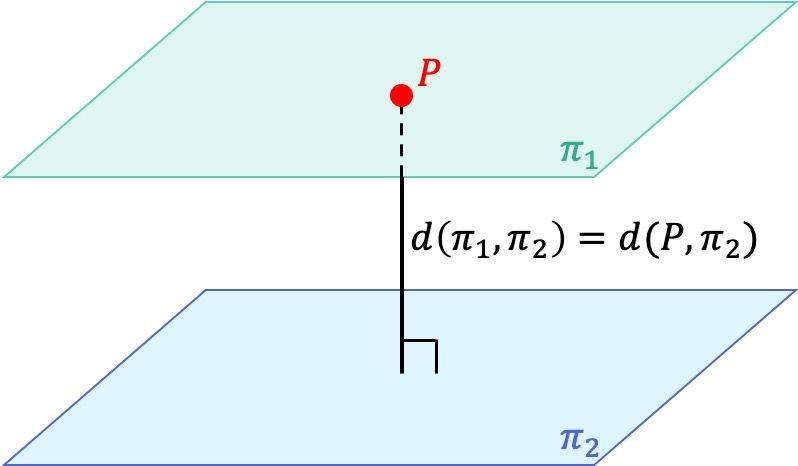
De manera que la fórmula para calcular la distancia entre dos planos paralelos es:

Sean dos planos paralelos, dados un punto de uno de los planos y la ecuación general (o implícita) del otro plano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

La fórmula para hallar la distancia entre dos planos paralelos mediante el punto de un plano y la ecuación general del otro plano es:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Esta es una fórmula que sirve para hallar la distancia entre dos planos paralelos. Sin embargo, en ocasiones podemos utilizar otro método aún más fácil:

Los coeficientes A, B y C de las ecuaciones implícitas (o generales) de dos planos deben ser proporcionales. Pues si en algún problema nos encontramos con dos planos cuyos coeficientes A, B y C son exactamente iguales, podemos usar otra fórmula sin necesidad de conocer ningún punto de algún plano:

Sean las ecuaciones generales (o implícitas) de dos planos paralelos con los coeficientes A, B y C idénticos:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La fórmula para hallar la distancia entre los dos planos paralelos a partir de las ecuaciones generales de los dos planos es:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

En definitiva, hay dos formas de encontrar la distancia entre dos planos paralelos. La primera es más útil cuando conocemos un punto de alguno de los dos planos. Sin embargo, si conocemos la ecuación general de los dos planos es mejor calcular la distancia con la segunda fórmula.

Ejemplo de cómo hallar la distancia entre dos planos paralelos

A modo de ejemplo, vamos a calcular la distancia entre los siguientes dos planos:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

En primer lugar, debemos comprobar que se trata de dos planos paralelos. Así pues, todos los coeficientes de las ecuaciones de los planos son proporcionales excepto los términos independientes, por lo que efectivamente son dos planos paralelos.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

En este caso los términos A, B y C de las ecuaciones de los dos planos no coinciden, pero podemos lograrlo dividiendo toda la ecuación del segundo plano entre dos:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

De modo que las ecuaciones de los dos planos ahora ya tienen los mismos coeficientes A, B y C. Por tanto, podemos calcular fácilmente la distancia entre ambos planos con la siguiente fórmula de la distancia entre 2 planos paralelos:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Sustituimos los valores y resolvemos las operaciones:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

De forma que la distancia entre un plano y el otro plano es igual a la unidad.

Ejercicios resueltos de distancia entre dos planos

Ejercicio 1

Encuentra la distancia entre los siguientes dos planos:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

Ver solución

Primero de todo, debemos comprobar que se trata de dos planos paralelos. Todos los coeficientes de las ecuaciones de los dos planos son proporcionales excepto los términos independientes, por lo que efectivamente se trata de dos planos paralelos.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

En este caso calcularemos la distancia entre los dos planos con la fórmula directa, ya que sus coeficientes A, B y C son iguales:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Entonces, sustituimos los valores en la fórmula y hacemos las operaciones:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Ejercicio 2

Calcula la distancia entre los siguientes dos planos:

$\pi_1 : \ 3x-2y+6z+4=0 \qquad \qquad \pi_2 : \ 6x-4y+3z+1=0$

Ver solución

Antes de nada, debemos verificar que se trata de dos planos paralelos para poder determinar la distancia que hay entre ellos. Para ello, comprobamos la proporcionalidad entre los coeficientes de los dos planos:

$\cfrac{3}{6}=\cfrac{-2}{-4}\neq\cfrac{6}{3} \neq \cfrac{4}{1} \quad \longrightarrow \quad \pi_1 \ \cancel{\parallel} \ \pi_2$

Pero los coeficientes A, B y C de los dos planos no son proporcionales, solamente los parámetros A y B. Por lo tanto, los dos planos no son paralelos sino secantes y, en consecuencia, la distancia entre ambos es igual a 0:

$\bm{d(\pi_1,\pi_2)=0}$

Ejercicio 3

Averigua la distancia entre los siguientes dos planos paralelos:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

Ver solución

El primer plano está definido en forma de ecuaciones paramétricas, por lo que para aplicar la fórmula directa de la distancia entre dos planos paralelos primero deberíamos pasarlo a forma de ecuación general y esto conlleva muchos cálculos y tiempo. Por tanto, es más rápido si cogemos un punto de ese plano y calculamos la distancia de dicho punto hasta el otro plano.

Así pues, las coordenadas de un punto que pertenece al plano π₁ corresponden a los términos independientes de cada ecuación paramétrica:

$P(3,-2,5)$