En esta página encontrarás cuáles son todas las posiciones relativas posibles de dos planos (planos secantes, paralelos o coincidentes). También hallarás cómo se calcula la posición relativa entre dos planos y, además, podrás ver ejemplos y practicar con ejercicios resueltos.
Índice
¿Cuáles son las posiciones relativas de dos planos?
En geometría analítica, solo existen tres posibles posiciones relativas entre dos planos: planos secantes, planos paralelos y planos coincidentes.
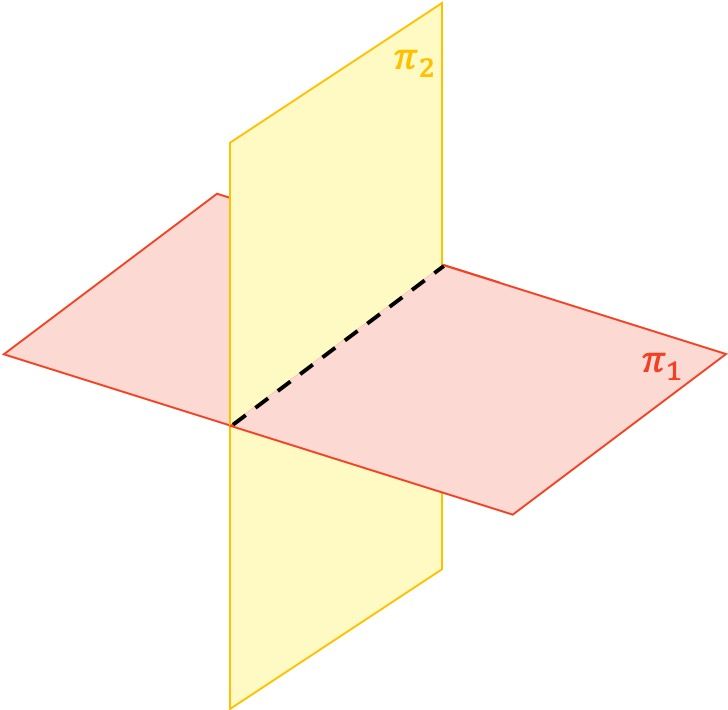
- Planos secantes: dos planos son secantes si solo se cortan en una recta.
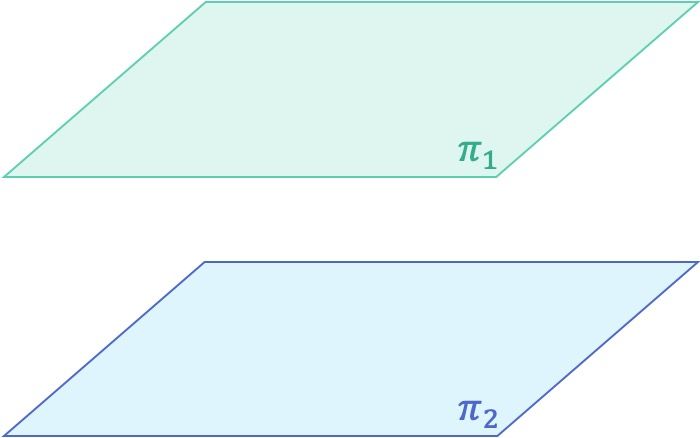
- Planos paralelos: dos planos son paralelos si no se cruzan en ningún punto.
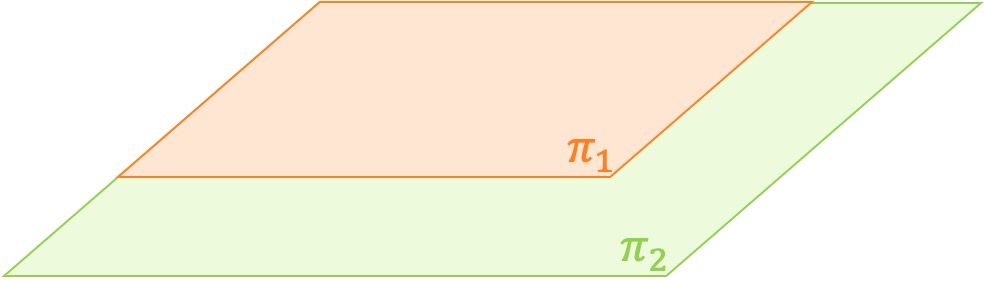
- Planos coincidentes: dos planos son coincidentes si tienen todos los puntos en común.
Planos secantes
Planos paralelos
Planos coincidentes
Existen dos métodos para encontrar la posición relativa entre dos planos: uno es a partir de los coeficientes de las ecuaciones generales de los dos planos y el otro es calculando los rangos de dos matrices. A continuación tienes la explicación de cada procedimiento.
Cómo determinar la posición relativa de dos planos por coeficientes
Una manera de averiguar cuál es la posición relativa entre dos planos es a través de los coeficientes de sus ecuaciones generales (o implícitas).
Entonces, sea la ecuación general (o implícita) de dos planos diferentes:
La posición relativa entre los dos planos en un espacio tridimensional (en R3) depende de la proporcionalidad de sus coeficientes o parámetros:
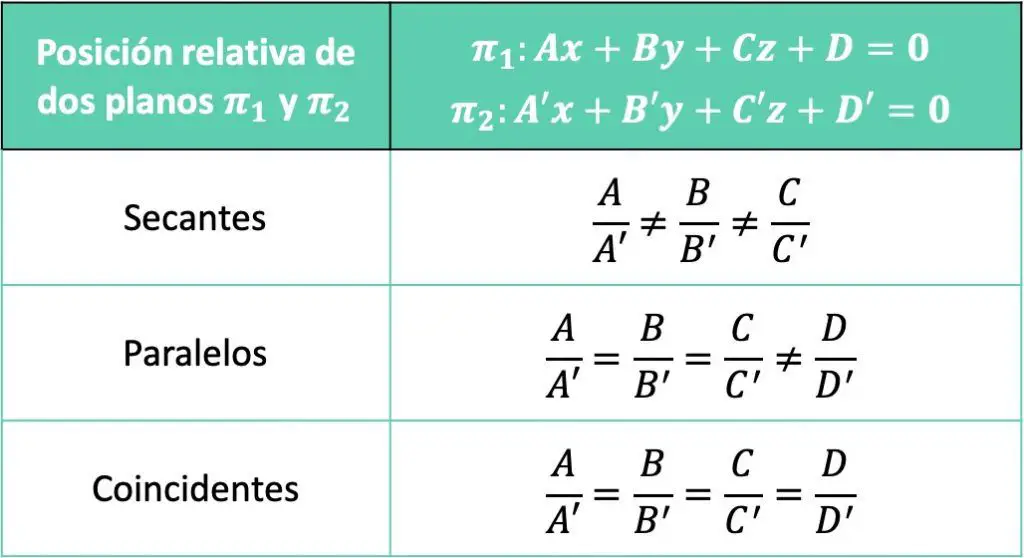
Por tanto, los dos planos serán secantes cuando alguno de los coeficientes A, B o C no sea proporcional con los otros. En cambio, los dos planos serán paralelos cuando únicamente los términos independientes no sean proporcionales. Y, por último, los planos serán coincidentes cuando todos los coeficientes de las dos ecuaciones sean proporcionales.
Por ejemplo, vamos a calcular la posición relativa de los siguientes dos planos:
Para saber qué tipo de planos son, debemos comprobar qué coeficientes son proporcionales:
Los coeficientes A, B y C son proporcionales entre sí pero no con el coeficiente D, por tanto, los dos planos son paralelos.
Cómo calcular la posición relativa de dos planos por rangos
Otra forma de hallar la posición relativa de dos planos determinados es calculando el rango de dos matrices formadas por los coeficientes de dichos planos.
Así pues, sea la ecuación general (o implícita) de dos planos distintos:
Llamamos A la matriz compuesta por los coeficientes A, B y C de ambas ecuaciones:
![\displaystyle A =\begin{pmatrix} A&B&C\\[1.1ex] A&B&C\end{pmatrix}](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-027869e94e5f904393a785965f907c34_l3.svg "Rendered by QuickLaTeX.com")
Y sea la matriz A’ la matriz ampliada con todos los coeficientes de las dos ecuaciones:
![\displaystyle A' =\begin{pmatrix} A&B&C&D\\[1.1ex] A&B&C&D'\end{pmatrix}](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-efc01167826bfc7763498b1999009d24_l3.svg "Rendered by QuickLaTeX.com")
Se puede conocer la posición relativa de los dos planos en función de los rangos de las dos matrices anteriores:
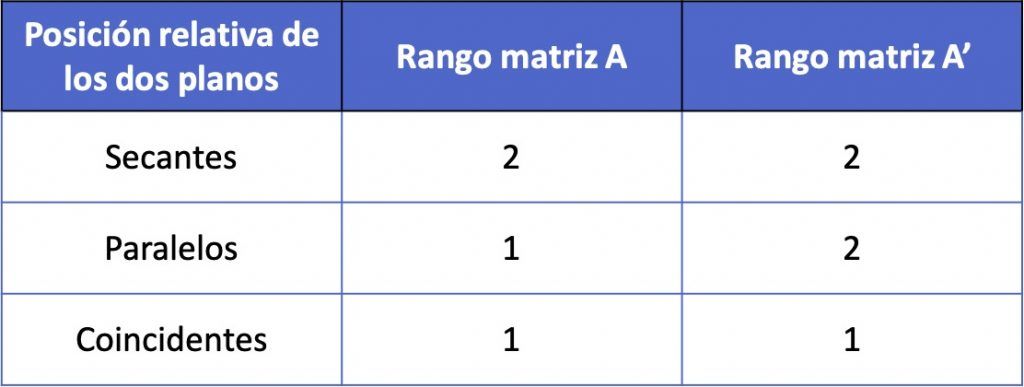
Que las posiciones relativas dependen de los rangos de estas dos matrices se puede demostrar a partir del toerema de Rouché-Frobenius (un teorema que sirve para resolver sistemas de ecuaciones lineales). Sin embargo, en esta página no haremos la demostración porque no es necesario saberla y tampoco aporta demasiado.
Para que veas cómo se hace, vamos a calcular la posición relativa entre los siguientes dos planos:
Lo primero que debemos hacer es construir la matriz A y la matriz ampliada A’ con los coeficientes de las ecuaciones de ambos planos:
![\displaystyle A =\begin{pmatrix} 2&3&-1\\[1.1ex] 3&-4&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&3&-1&1\\[1.1ex] 3&-4&0&2\end{pmatrix}](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-fb79757aaea591bd81493f3d5c3c85e6_l3.svg "Rendered by QuickLaTeX.com")
Y ahora tenemos que calcular el rango de cada matriz. Primero hallamos el rango de la matriz A por determinantes:
![\displaystyle \begin{vmatrix} 2&3\\[1.1ex] 3&-4\end{vmatrix} =-17\neq 0](https://www.geometriaanalitica.info/wp-content/ql-cache/quicklatex.com-da5375d6bd25cf30892c2d20b7430292_l3.svg "Rendered by QuickLaTeX.com")
La matriz A contiene una submatriz 2×2 cuyo determinante es diferente de cero, con lo que se trata de una matriz de rango 2.
Por otro lado, también tenemos que calcular el rango de la matriz A’. Y el rango de la matriz ampliada A’ siempre será como mínimo el mismo de la matriz A, por lo tanto, en este caso concreto el rango de la matriz A’ también es igual a 2.
De modo que el rango de las dos matrices son equivalentes y de valor 2, por tanto, los dos planos son secantes.
Ejercicios resueltos de la posición relativa de dos planos
Ejercicio 1
Estudia la posición relativa de los siguientes dos planos:
Para calcular la posición relativa entre los dos planos, vamos a ver si los coeficientes de las ecuaciones de los dos planos son proporcionales:
Todos los coeficientes de las ecuaciones implícitas de los dos planos son proporcionales entre sí, por lo que se trata de dos planos coincidentes.
Ejercicio 2
Determina la posición relativa de los siguientes dos planos:
Con tal de determinar la posición relativa entre los dos planos, vamos a analizar la proporcionalidad de los coeficientes de sus ecuaciones:
Los coeficientes A y C de las ecuaciones implícitas de los dos planos son proporcionales entre sí, pero no con el coeficiente B. Así que se trata de dos planos secantes.
Ejercicio 3
Halla la posición relativa de los siguientes 2 planos:
Para determinar la posición relativa entre los dos planos, debemos verificar si los coeficientes de las ecuaciones de los dos planos son proporcionales:
Los tres primeros parámetros (A, B y C) de las ecuaciones de los dos planos son proporcionales entre sí pero no con el parámetro D, de manera que los dos planos son paralelos.
Ejercicio 4
Calcula el valor del parámetro 
para que los siguientes dos planos sean paralelos:
Para que los dos planos sean paralelos, los coeficientes A, B y C de sus ecuaciones deben ser proporcionales. Es decir, se tiene que cumplir la siguiente igualdad:
En este caso en particular, los coeficientes A y B del primer plano son la mitad que los del segundo plano:
Por lo tanto, debemos resolver la ecuación anterior. Y, para ello, multiplicamos en cruz las dos fracciones:
De modo que el valor del parámetro tiene que ser igual a 10.
