▷ El Plano (geometría): qué es, características, ejemplos,...

En esta página encontrarás la explicación de qué es un plano, de cómo se calcula y de todas sus propiedades. Además, podrás ver ejemplos de planos, cuáles son las posiciones relativas entre dos planos, cómo determinar el ángulo que forman 2 planos y, por último, cómo expresar numéricamente cualquier plano mediante las ecuaciones del plano.

Índice

¿Qué es un plano?

En geometría analítica, la definición del plano es la siguiente:

Un plano es un objeto geométrico que tiene dos dimensiones (longitud y anchura).

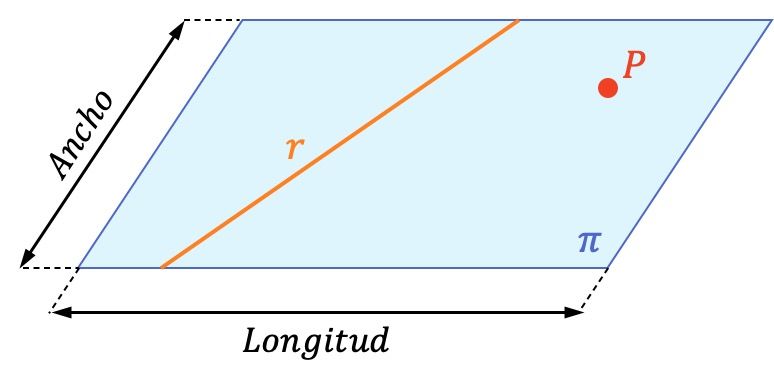
Por lo tanto, un plano contiene infinitas rectas e infinitos puntos. En la representación gráfica de arriba puedes ver la diferencia entre un plano, una recta y un punto. Además, puedes comprobar que la recta $r$ y el punto $P$ están contenidos en el plano $\pi.$

Como puedes apreciar en el plano representado gráficamente, los planos se suelen nombrar con letras griegas: $\pi, \alpha, \beta,...$

Un ejemplo de un plano que utilizamos mucho en matemáticas es el plano cartesiano. El plano cartesiano se trata del plano que queda definido por el eje de las abscisas (eje X) y el eje de las ordenadas (eje Y). Una de las utilidades del plano cartesiano es que sirve para describir la posición de un objeto en un sistema de referencia.

Determinación de un plano

Una vez hemos visto el significado de un plano, veamos cómo se puede determinar cualquier plano en el espacio tridimensional (en R3).

Un plano queda completamente determinado por los siguientes elementos geométricos:

Tres puntos no alineados.
Una recta y un punto exterior a ella.
Dos rectas paralelas o dos rectas secantes.

Respecto al último punto, seguro que ya sabes qué significa que dos rectas sean paralelas. Pero el significado de las rectas secantes es menos conocido, así que si tienes alguna duda aquí puedes consultar qué son las rectas secantes.

Por lo tanto, si tenemos cualquier condición de las 3 anteriores significa que podemos formar un plano.

Propiedades del plano

El plano cumple con las siguientes características:

Un plano contiene infinitos puntos.
Un plano contiene infinitas rectas.
Un plano es ilimitado, es decir, es una superficie que se extiende en el espacio ilimitadamente.
Dos planos que se cortan determinan una recta.
Una recta que tiene un punto en un plano no necesariamente está contenida en él. Para que una recta forme parte de un plano debe tener, como mínimo, dos puntos en el plano.
Por una recta pasan infinitos planos.
Un semiplano es cada una de las 2 partes en que queda dividido un plano al cortarlo por cualquiera de sus rectas.

Ecuaciones del plano

En geometría analítica, la ecuación de un plano es una ecuación que permite expresar matemáticamente cualquier plano. De modo que para hallar la ecuación de un plano solo se necesita un punto y dos vectores linealmente independientes que pertenezcan a dicho plano.

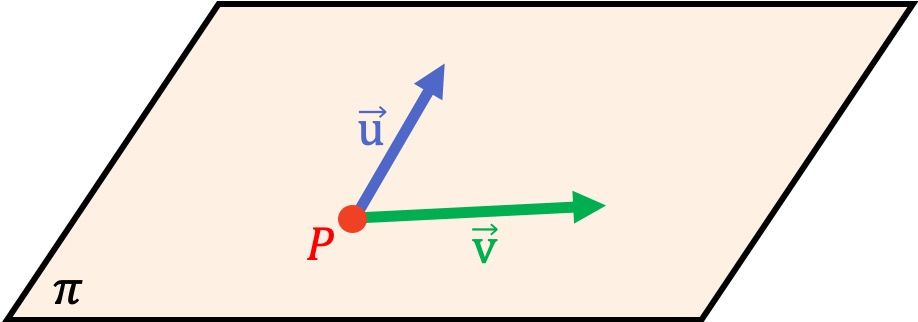
Sin embargo, como hemos visto arriba en la explicación del concepto de un plano, existen varias formas de determinar un plano. Pues, del mismo modo, también hay diferentes maneras de expresar analíticamente un plano.

De modo que todos los tipos de ecuaciones del plano son: la ecuación vectorial, las ecuaciones paramétricas, la ecuación implícita (o general) y la ecuación canónica (o segmentaria) del plano.

A continuación vamos a ver detalladamente la explicación y la fórmula de todas las ecuaciones del plano.

Ecuación vectorial del plano

Dados un punto y dos vectores directores de un plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La fórmula de la ecuación vectorial de un plano es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

O, equivalentemente:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Donde $\lambda$ y $\mu$ son dos escalares, es decir, dos números reales.

Ecuaciones paramétricas del plano

La fórmula de la ecuación paramétrica de un plano es la siguiente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Donde:

$\lambda$ y $\mu$ son dos escalares, es decir, dos números reales.
$\text{u}_x,\text{u}_y,\text{u}_z$ son las componentes de uno de los dos vectores directores del plano $\vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z).$
$\text{v}_x,\text{v}_y,\text{v}_z$ son las componentes del otro vector director del plano $\vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z).$

Ecuación implícita o general del plano

Dados un punto y dos vectores directores de un plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La ecuación implícita, general o cartesiana de un plano se obtiene resolviendo el siguiente determinante e igualando el resultado a 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

De modo que la ecuación implícita o general del plano resultante será de la siguiente forma:

Este tipo de ecuación del plano también se llama ecuación cartesiana del plano.

Ecuación canónica o segmentaria del plano

La fórmula de la ecuación canónica o segmentaria de un plano es la siguiente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Donde:

$a$ es el punto de intersección entre el plano y el eje X.
$b$ es el punto de corte entre el plano y el eje Y.
$c$ es donde se cortan el plano con el eje Z.

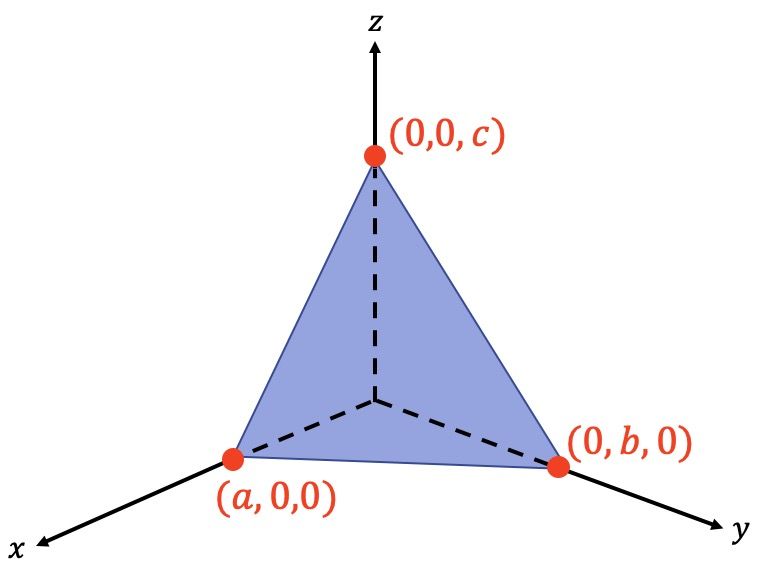
ecuacion segmentaria o canonica del plano bachillerato

La ecuación canónica (o ecuación segmentaria) del plano, también se puede obtener a partir de su ecuación general:

$Ax+By+Cz+D=0$

En primer lugar, despejamos el coeficiente D de la ecuación:

$Ax+By+Cz=-D$

Luego dividimos toda la ecuación del plano entre el valor del parámetro D cambiado de signo:

$\cfrac{Ax+By+Cz}{-D}=\cfrac{-D}{-D}$

$\cfrac{Ax}{-D}+\cfrac{By}{-D}+\cfrac{Cz}{-D}=1$

Y, mediante las propiedades de las fracciones, llegamos a la siguiente expresión:

$\cfrac{x}{-\frac{D}{A}}+\cfrac{y}{-\frac{D}{A}}+\cfrac{z}{-\frac{D}{A}}=1$

Por lo tanto, de esta expresión se deducen las fórmulas para calcular directamente los términos de la ecuación canónica o segmentaria de un plano:

$a=-\cfrac{D}{A} \qquad b=-\cfrac{D}{B} \qquad c=-\cfrac{D}{C}$

En consecuencia, para poder formar esta variante de las ecuaciones del plano es necesario que los coeficientes A, B y C sean diferentes de cero, evitando de esta manera las indeterminaciones de las fracciones.

Posición relativa de dos planos

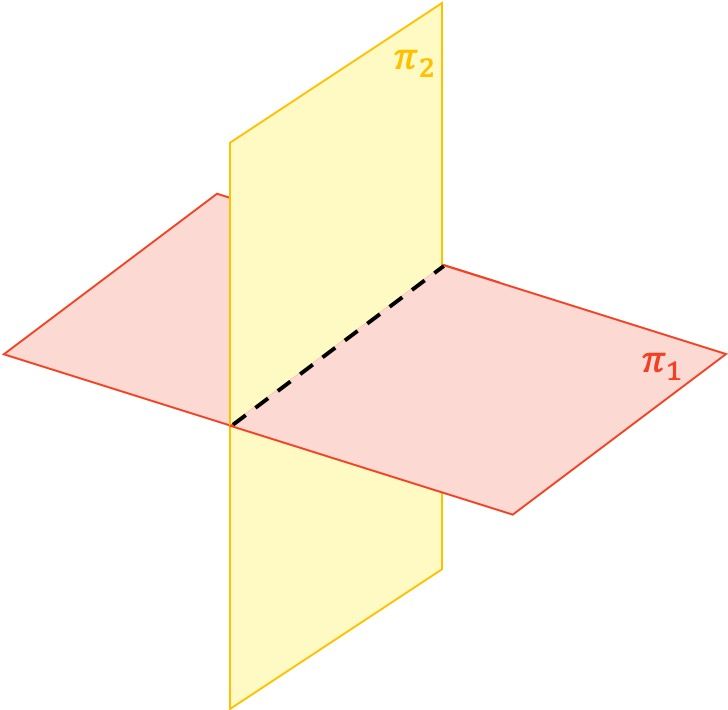
En geometría analítica, solo existen tres posibles posiciones relativas entre dos planos: planos secantes, planos paralelos y planos coincidentes.

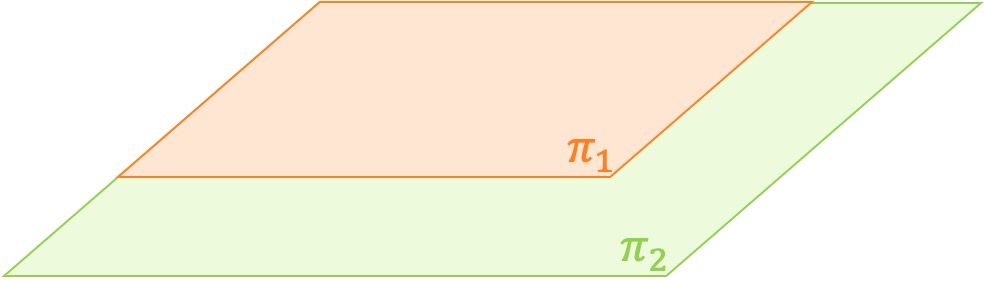
Planos secantes: dos planos son secantes si solo se cortan en una recta.
Planos paralelos: dos planos son paralelos si no se intersecan en ningún punto.
Planos coincidentes: dos planos son coincidentes si tienen todos los puntos en común.

Planos secantes

Planos paralelos

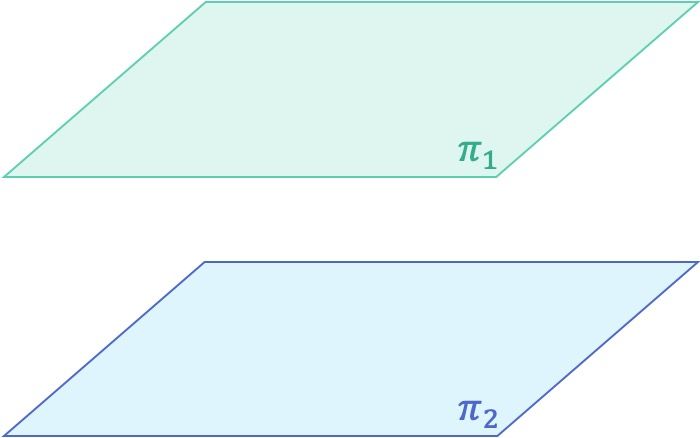
Planos coincidentes

Además, si dos planos secantes se cortan formando un ángulo de 90º, se trata de dos planos perpendiculares entre sí.

Ángulo entre dos planos

El ángulo entre dos planos es igual al ángulo que forman los vectores normales de dichos planos. Por tanto, para hallar el ángulo entre dos planos se calcula el ángulo que forman sus vectores normales, ya que son equivalentes.

Así pues, una vez sabemos exactamente en qué consiste el ángulo entre dos planos, veamos la fórmula para calcular el ángulo entre dos planos en el espacio, que se deduce a partir de la fórmula del ángulo entre dos vectores:

Dada la ecuación general (o implícita) de dos planos distintos:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

El vector normal de cada plano es:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

Y el ángulo que forman estos dos planos se determina calculando el ángulo que forman sus vectores normales mediante la siguiente fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Evidentemente, una vez hemos calculado el coseno del ángulo que forman los dos planos a partir de la fórmula, debemos invertir el coseno para hallar el valor dicho ángulo.

Por otro lado, cuando los dos planos son perpendiculares o paralelos no es necesario aplicar la fórmula, porque el ángulo entre los 2 planos se puede determinar directamente:

El ángulo entre dos planos paralelos es de 0º, ya que sus vectores normales tienen la misma dirección.
El ángulo entre dos planos perpendiculares es de 90º, debido a que sus vectores normales también son perpendiculares (u ortogonales) entre sí y, por lo tanto, forman un ángulo recto.

El plano (geometría)