Ecuaciones paramétricas de la recta

En esta página encontrarás cómo calcular las ecuaciones paramétricas de cualquier recta, ya sea a partir de un punto y un vector o a partir de dos puntos. También hallarás cómo conseguir diferentes puntos de una recta con sus ecuaciones paramétricas. Y, además, podrás ver varios ejemplos y practicar con ejercicios resueltos.

Cómo hallar las ecuaciones paramétricas de la recta

Para determinar las ecuaciones paramétricas de cualquier recta tan solo se necesita su vector director y un punto que pertenezca a la recta.

Si \vv{\text{v}} es el vector director de la recta y P un punto que pertenece a la recta:

\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)

La fórmula de las ecuaciones paramétricas de la recta son:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

Donde:

  • x e y son las coordenadas cartesianas de cualquier punto de la recta.
  • P_1 y P_2 son las coordenadas de un punto conocido que forma parte de la recta.
  • \text{v}_1 y \text{v}_2 son las componentes del vector director de la recta.
  • t es un escalar (un número real) cuyo valor depende de cada punto de la recta.

Por lo tanto, las ecuaciones paramétricas son una forma de expresar analíticamente una recta.

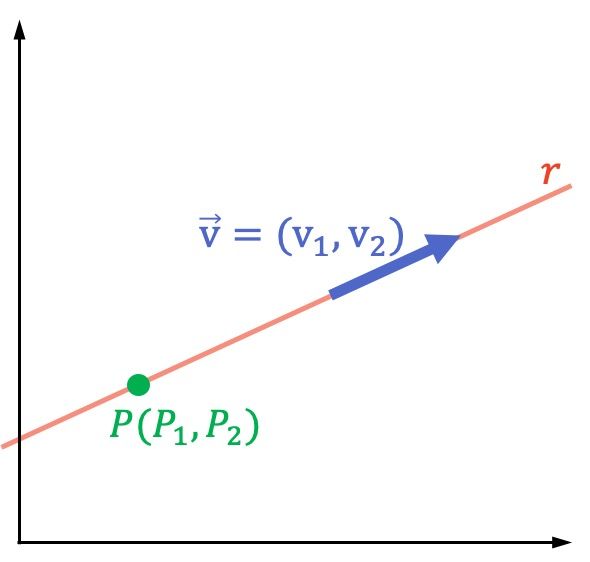
ecuaciones parametricas de la recta 3 dimensiones

Esta son las ecuaciones paramétricas de la recta en el plano, es decir, cuando trabajamos con puntos y vectores de 2 coordenadas (en R2). Sin embargo, si estuviésemos haciendo cálculos en el espacio (en R3) tendríamos que añadir una ecuación más para la tercera componente Z:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}

Por otro lado, ten en cuenta que a parte de las ecuaciones paramétricas, existen más maneras de describir matemáticamente a una recta: la ecuación vectorial, la ecuación continua, la ecuación implícita (o general), la ecuación explícita y la ecuación punto-pendiente de una recta. Puedes consultar en qué consiste cada una de ellas en nuestra web.

Ejemplo de cómo determinar las ecuaciones paramétricas de la recta

Veamos ahora cómo se encuentran las ecuaciones paramétricas de una recta a partir de un ejemplo:

  • Escribe las ecuaciones paramétricas de la recta que pasa por el punto P y tiene \vv{\text{v}} como vector director:

\vv{\text{v}}= (3,-2) \qquad P(4,1)

Para calcular las ecuaciones paramétricas de la recta tenemos que aplicar su fórmula:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

Por lo tanto, sustituimos las coordenadas del punto y del vector director en la fórmula:

\displaystyle \begin{cases} x=4+t\cdot 3 \\[1.7ex] y=1+t\cdot(-2) \end{cases}

\displaystyle \begin{cases} x=4+3t \\[1.7ex] y=1-2t \end{cases}

Obtener puntos a partir de las ecuaciones paramétricas de la recta

Cuando ya hemos hallado las ecuaciones paramétricas de la recta, es muy fácil calcular puntos por los que pase dicha recta. Para determinar un punto de una recta se debe otorgar un valor al parámetro \bm{t} de las ecuaciones paramétricas de la recta.

Por ejemplo, dadas las siguientes ecuaciones paramétricas de la recta:

\displaystyle \begin{cases} x=2+t \\[1.7ex] y=-1+3t \end{cases}

Podemos conseguir un punto de la recta sustituyendo t por un número cualquiera, por ejemplo t=1:

\displaystyle \begin{cases} x=2+1= 3 \\[1.7ex] y=-1+3\cdot 1=2 \end{cases}

\bm{A(3,2)}

Y podemos calcular otro punto de la recta si sustituimos la variable t por un número diferente, por ejemplo t=2:

\displaystyle \begin{cases} x=2+2= 4 \\[1.7ex] y=-1+3\cdot 2=5 \end{cases}

\bm{B(4,5)}

Por lo tanto, podemos conseguir infinitos puntos de la recta, porque la variable t puede tomar infinitos valores.

Cómo calcular las ecuaciones paramétricas de la recta a partir de dos puntos

Otro problema típico de las ecuaciones paramétricas es que nos dan 2 puntos que pertenecen a la recta y a partir de ellos debemos calcular las ecuaciones paramétricas. Veamos cómo se resuelve mediante un ejemplo:

  • Halla las ecuaciones paramétricas de la recta que pasa por los siguientes dos puntos:

A(2,4) \qquad B(5,-3)

Como hemos visto en los apartados de arriba, para hallar las ecuaciones paramétricas de una recta necesitamos su vector director y un punto suyo. Ya tenemos un punto de la recta, pero nos falta su vector director. De modo que primero debemos calcular el vector director de la recta y luego las ecuaciones paramétricas.

Para encontrar el vector director de la recta, basta con calcular el vector que definen los dos puntos dados en el enunciado:

\vv{AB} = B - A = (5,-3) - (2,4) = (3,-7)

Y una vez también sabemos el vector director de la recta, para hallar sus ecuaciones paramétricas simplemente debemos aplicar la fórmula:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

\displaystyle \begin{cases} x=2+t\cdot 3 \\[1.7ex] y=4+t\cdot(-7) \end{cases}

\displaystyle \begin{cases} x=2+3t \\[1.7ex] y=4-7t \end{cases}

En este caso hemos cogido el punto A para definir las ecuaciones paramétricas, pero también es correcto escribirlas con el otro punto que nos dan en el enunciado:

\displaystyle \begin{cases} x=5+3t \\[1.7ex] y=-3-7t \end{cases}

Ejercicios resueltos de ecuaciones paramétricas de la recta

Ejercicio 1

Halla la ecuación paramétrica de la recta cuyo vector director es \vv{\text{v}} y pasa por el punto P:

\vv{\text{v}}= (-1,-2) \qquad P(5,0)

Para hallar las ecuaciones paramétricas de la recta simplemente debemos aplicar su fórmula:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

\displaystyle \begin{cases} x=5+t\cdot (-1) \\[1.7ex] y=0+t\cdot(-2) \end{cases}

\displaystyle \begin{cases} x=5-t \\[1.7ex] y=-2t \end{cases}

 

Ejercicio 2

Calcula dos puntos diferentes de la siguiente recta definida mediante las ecuaciones paramétricas:

\displaystyle \begin{cases} x=1+5t \\[1.7ex] y=-4-3t \end{cases}

Para conseguir puntos de una recta expresada con las ecuaciones paramétricas, se debe otorgar valores al parámetro t.

Por tanto, para calcular un primer punto sustituimos la incógnita t por ejemplo por t=0:

\displaystyle \begin{cases} x=1+5\cdot 0 = 1 \\[1.7ex] y=-4-3\cdot 0 = -4 \end{cases}

\bm{A(1,-4)}

Y para averiguar un segundo punto de la recta damos a t por ejemplo el valor de t=1:

\displaystyle \begin{cases} x=1+5\cdot 1 = 6 \\[1.7ex] y=-4-3\cdot 1 = -7 \end{cases}

\bm{B(6,-7)}

Puede que hayas obtenido distintos puntos, ya que esto depende de los valores que le des al parámetro t. Pero si has seguido el mismo procedimiento está bien.

 

Ejercicio 3

Dado el siguiente punto:

P(3,-1)

Determina si dicho punto pertenece o no a la siguiente recta:

\displaystyle \begin{cases} x=-3+2t \\[1.7ex] y=1+2t \end{cases}

Para comprobar si el punto pertenece a la recta, debemos sustituir sus coordenadas en las ecuaciones de la recta y ver si de cada ecuación hallamos el mismo valor del parámetro t. En tal caso, significará que el punto forma parte de la recta, de lo contrario implica que la recta no pasa por ese punto.

Así pues, sustituimos las coordenadas del punto en las ecuaciones paramétricas de la recta:

\displaystyle \begin{cases} 3=-3+2t \\[1.7ex] -1=1+2t \end{cases}

Y solucionamos las dos ecuaciones resultantes:

Coordenada X

3 = -3 +2t

3+3 = 2t

6=2t

\cfrac{6}{2}=t

3=t

Coordenada Y

-1 = 1 +2t

-1-1 = 2t

-2=2t

\cfrac{-2}{2}=t

-1=t

Hemos obtenido dos valores de t diferentes, por lo que el punto no pertenece a la recta.

 

Ejercicio 4

Calcula las ecuaciones paramétricas de la recta que pasa por los siguientes dos puntos:

A(-1,4) \qquad B(-2,4)

Para calcular las ecuaciones paramétricas de una recta necesitamos conocer su vector director y uno de sus puntos. En este caso ya tenemos un punto de la recta, pero nos falta su vector director. De manera que primero debemos calcular el vector director de la recta y luego las ecuaciones paramétricas.

Para encontrar el vector director de la recta, basta con calcular el vector que definen los dos puntos dados en el enunciado:

\vv{AB} = B - A = (-2,4) - (-1,4) = (-1,0)

Y una vez ya sabemos el vector director de la recta, para hallar sus ecuaciones paramétricas simplemente aplicamos la fórmula:

\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}

\displaystyle \begin{cases} x=-1+t\cdot (-1) \\[1.7ex] y=4+t\cdot 0 \end{cases}

\displaystyle \begin{cases} x=-1-t\\[1.7ex] y=4 \end{cases}

En este caso hemos escogido el punto A para definir las ecuaciones paramétricas, pero también es válido escribirlas con el otro punto que nos dan en el enunciado:

\displaystyle \begin{cases} x=-2-t\\[1.7ex] y=4 \end{cases}

 

Aplicaciones de las ecuaciones paramétricas

Evidentemente, la utilidad principal de las ecuaciones paramétricas es definir rectas, tal y como hemos visto. Sin embargo, las ecuaciones paramétricas también sirven para describir otros tipos de elementos geométricos.

Por ejemplo, se puede expresar cualquier circunferencia mediante ecuaciones paramétricas. Si r es el radio de la circunferencia y C(x_0,y_0) son las coordenadas de su centro, la parametrización de una circunferencia es:

\displaystyle \begin{cases} x=x_0+r\cdot \text{cos}(t) \\[1.7ex] y=y_0+r\cdot\text{sen}(t) \end{cases}

Del mismo modo, también se puede parametrizar una elipse. Si C(x_0,y_0) son las coordenadas del centro de la elipse, a su radio horizontal y b su radio vertical, las ecuaciones paramétricas de una elipse son:

\displaystyle \begin{cases} x=x_0+a\cdot \text{cos}(t) \\[1.7ex] y=y_0+b\cdot\text{sen}(t) \end{cases}

Asimismo, se puede hacer la representación paramétrica de otras curvas, como por ejemplo una parábola o incluso una hipérbola. Aunque no las mostramos en este artículo ya que son bastante más complicadas.

Finalmente, un plano también se puede definir mediante una expresión paramétrica. De hecho, las ecuaciones paramétricas de un plano son:

\displaystyle \begin{cases} x=x_0+\lambda\cdot \text{u}_1 + \mu \cdot \text{v}_1 \\[1.7ex] y=y_0+\lambda\cdot \text{u}_2 + \mu \cdot \text{v}_2 \\[1.7ex] z=z_0+\lambda\cdot \text{u}_3 + \mu \cdot \text{v}_3 \end{cases}

Siendo P(x_0,y_0,z_0) un punto fijo del plano, los coeficientes \lambda y \mu dos parámetros incógnitas, y \vv{\text{u}}= (\text{u}_1,\text{u}_2) y \vv{\text{v}}=(\text{v}_1,\text{v}_2) dos vectores de direcciones diferentes contenidos en el plano.

2 comentarios en “Ecuaciones paramétricas de la recta”

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio