En esta página encontrarás la fórmula de la ecuación punto-pendiente de la recta y, también, las distintas maneras que existen para calcularla. Además, podrás ver varios ejemplos y practicar con ejercicios resueltos paso a paso.
Índice
Fórmula de la ecuación punto-pendiente de la recta
La ecuación punto-pendiente de la recta es una forma de expresar matemáticamente una recta. En particular, solo se necesita la pendiente y las coordenadas de un punto de la recta para hallar la ecuación punto-pendiente de una recta.
La fórmula de la ecuación punto-pendiente de la recta es:
Donde es la pendiente de la recta y
son las coordenadas de un punto que pertenece a la recta
Veamos cómo se calcula la ecuación punto-pendiente de la recta mediante un ejemplo:
- Escribe la ecuación punto-pendiente de la recta que pasa por el punto
y tiene como pendiente m=3.
La fórmula de la ecuación punto-pendiente de la recta es:
En este caso, el enunciado nos dice que la pendiente de la recta es m=3, por lo que la ecuación de la recta será de la siguiente forma:
Además, también sabemos que la recta pasa por el punto , por lo tanto, debemos sustituir las coordenadas de este punto en la ecuación:
De modo que la ecuación punto-pendiente de la recta es:
Ten en cuenta que a parte de la ecuación punto-pendiente existen más formas de expresar analíticamente una recta: la ecuación vectorial, las ecuaciones paramétricas, la ecuación continua, la ecuación implícita (o general) y la ecuación explícita de una recta. Si estás más interesado puedes consultar en qué consiste cada una de ellas en nuestra web.
¿Qué significa la pendiente de una recta?
Como hemos visto en la definición de la ecuación punto-pendiente de una recta, el parámetro es la pendiente de la recta. Pero realmente… ¿cuál es el significado de la pendiente de una recta? Veámoslo a partir de la representación gráfica de una recta:
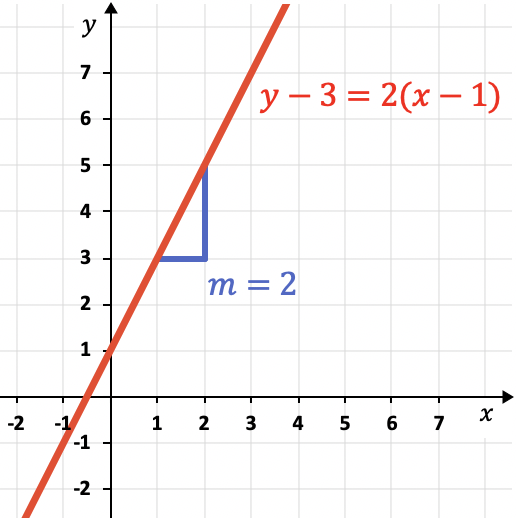
La pendiente de la recta indica su inclinación. Como ves en la recta de la gráfica, es igual a 2 ya que la recta sube 2 unidades verticales por cada 1 unidad horizontal.
Evidentemente, si la pendiente es positiva la función es creciente (va hacia arriba), en cambio, si la pendiente es negativa la función es decreciente (va hacia abajo).
Cómo se calcula la pendiente de una recta
A parte, existen 3 maneras distintas para determinar numéricamente la pendiente de una recta:
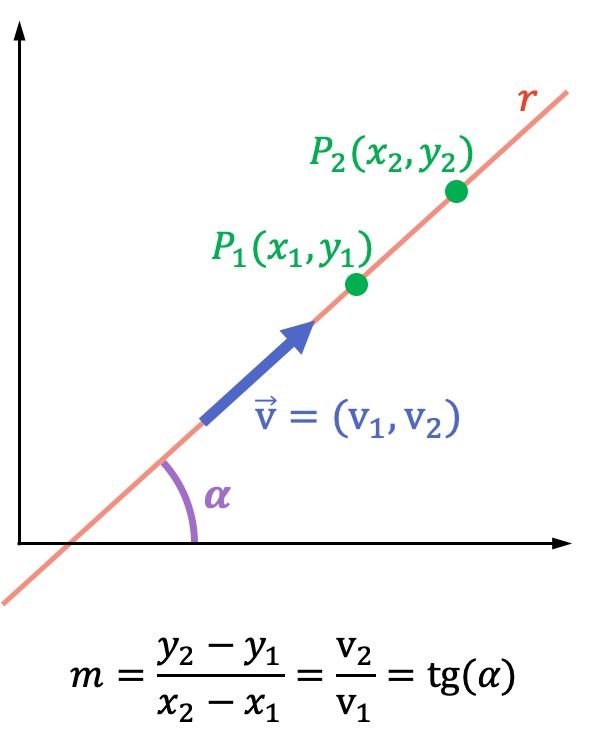
- Dados dos puntos diferentes de la recta
y
la pendiente de la recta es igual a:
- Si
es el vector director de la recta, su pendiente es:
- Si
es el ángulo que forma la recta con el eje de las abscisas (eje X), la pendiente de la recta es equivalente a la tangente de dicho ángulo:
Posición relativa de las rectas
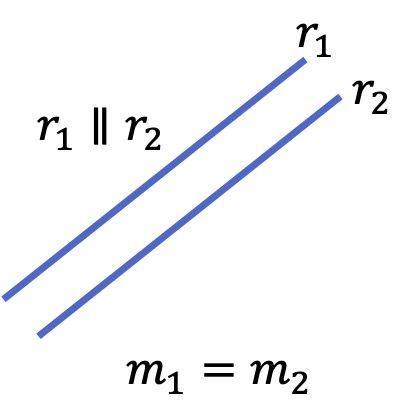
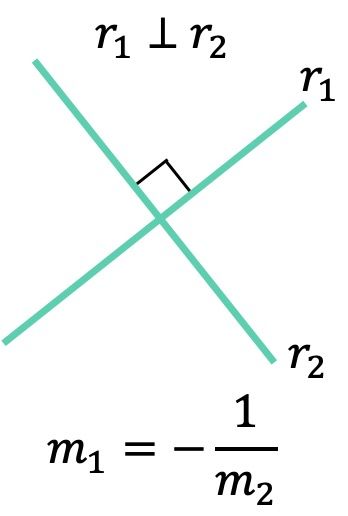
Finalmente, la pendiente de una recta también sirve para saber la relación que hay entre varias rectas. Ya que dos rectas paralelas tienen la misma pendiente y, por contra, si la pendiente de una recta es la inversa negativa de la pendiente de otra recta significa que esas dos rectas son perpendiculares.
Calcular la ecuación punto-pendiente de la recta que pasa por dos puntos
Un problema muy habitual es determinar la ecuación punto-pendiente a partir de dos puntos que pertenecen a la recta. Veamos cómo se resuelve a través de un ejemplo:
- Halla la ecuación punto-pendiente de la recta que pasa por los siguientes dos puntos:
Para hallar la ecuación punto-pendiente de la recta tenemos que averiguar cuánto vale la pendiente de la recta. Así que calculamos la pendiente de la recta mediante la fórmula de los dos puntos:
De manera que la ecuación punto-pendiente de la recta será de la siguiente forma:
Por tanto, solo nos queda sustituir las coordenadas cartesianas de un punto de la recta en la ecuación:
También está bien si ponemos en la ecuación de la recta el otro punto del enunciado:
Hallar la ecuación punto-pendiente de una recta a partir de la gráfica
Como hemos visto en los apartados de arriba, existen varias maneras de averiguar la ecuación punto-pendiente de una recta numéricamente. Sin embargo, también se puede encontrar gráficamente. Veamos cómo se hace a través de un ejemplo:
- Determina la ecuación punto-pendiente de la recta representada en el siguiente gráfico:
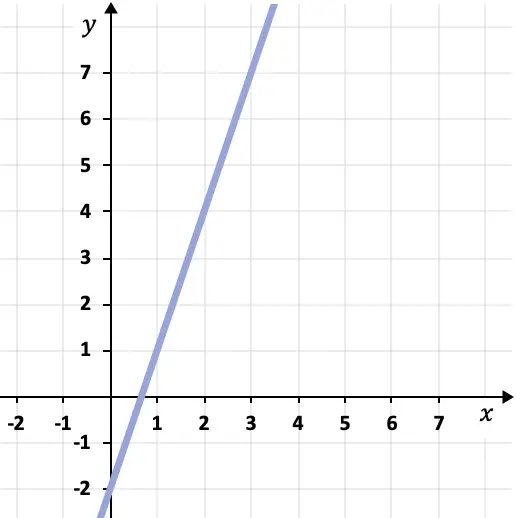
Para determinar la ecuación punto-pendiente de la recta representada gráficamente debemos hallar su pendiente y un punto de la recta.
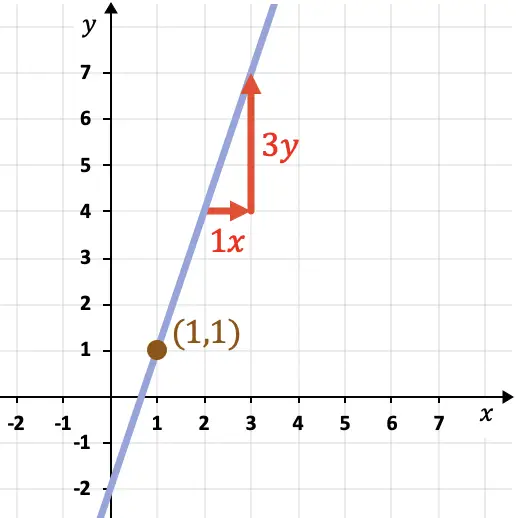
En este caso, la pendiente de la recta vale 3, porque la recta sube 3 unidades verticales por cada unidad horizontal.
Luego necesitamos un punto de la recta. Para ello, podemos escoger cualquier punto de la gráfica por los que pasa la recta, por ejemplo el punto (1,1).
Por tanto, ya podemos hallar la ecuación punto-pendiente de la recta aplicando su fórmula:
Ejercicios resueltos de la ecuación punto-pendiente de la recta
Ejercicio 1
Escribe la ecuación punto-pendiente de la recta que pasa por el punto y su pendiente es
La fórmula de la ecuación punto – pendiente de la recta es:
En este caso, el enunciado nos dice que la pendiente de la recta es m=-2, por lo que la ecuación de la recta será de la siguiente forma:
Además, también sabemos por el enunciado que la recta pasa por el punto , por lo tanto, solo nos queda sustituir las coordenadas del punto en la ecuación de la recta:
Ejercicio 2
¿Cuál es la ecuación punto-pendiente de la recta que pasa por los siguientes dos puntos?
Para encontrar la ecuación punto-pendiente de la recta tenemos que averiguar cuánto vale la pendiente de la recta. Así que calculamos la pendiente de la recta con su fórmula:
De manera que la ecuación punto-pendiente de la recta será de la siguiente forma:
Por tanto, solo nos queda sustituir las coordenadas de un punto de la recta en la ecuación:
También hubiese sido correcto poner en la ecuación el otro punto del enunciado:
Ejercicio 3
Calcula la ecuación punto-pendiente de la recta que pasa por los siguientes dos puntos:
Para hallar la ecuación punto-pendiente de la recta primero debemos calcular su pendiente:
De modo que la ecuación punto-pendiente de la recta será de la siguiente forma:
Por tanto, solo nos queda sustituir las coordenadas de un punto de la recta en la ecuación:
También es correcto poner en la ecuación de la recta el otro punto del enunciado:
Ejercicio 4
Calcula la ecuación punto-pendiente de la recta que forma un ángulo de 45º con el eje X y pasa por el origen de coordenadas.
Si la recta forma un ángulo de 45 grados con el eje OX, su pendiente será:
Y una vez sabemos la pendiente de la recta, podemos encontrar la ecuación punto-pendiente sustituyendo un punto de la recta en la ecuación. Además, el enunciado nos dice que la recta pasa por el origen de coordenadas, lo que significa que pasa por el punto (0,0). Por tanto:
De modo que la ecuación punto-pendiente de la recta es:
Ejercicio 5
Encuentra la ecuación punto pendiente de la recta paralela a la recta y que pasa por el punto
Siendo la recta
La pendiente de la recta es igual a 2 (número de delante del paréntesis), y para que dos rectas sean paralelas ambas deben tener la misma pendiente, por lo tanto:
Y una vez conocemos la pendiente de la recta, solo hace falta sustituir las coordenadas de un punto que pertenezca a la recta en la fórmula:
Por lo que la ecuación punto-pendiente de la recta es:
Ejercicio 6
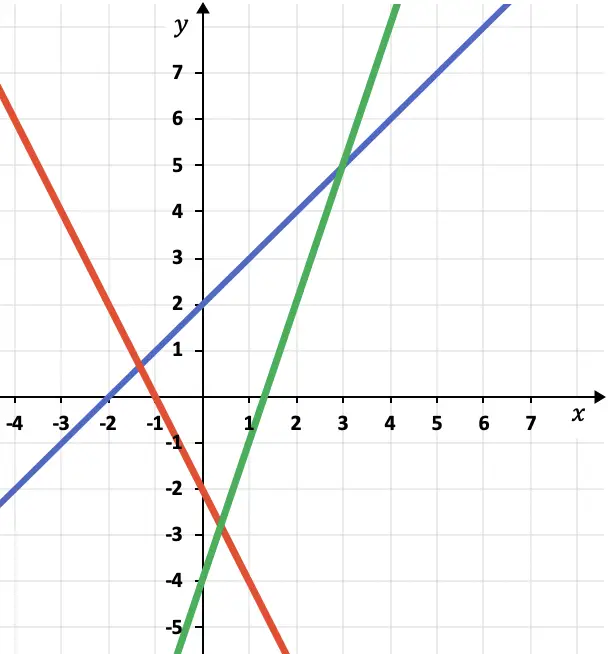
Determina la ecuación punto-pendiente de cada recta que está representada en la siguiente gráfica:
Recta azul
La recta azul aumenta una Y por cada X, por lo tanto, su pendiente es igual a 1. Por otro lado, pasa por el punto (2,4), por tanto:
Recta verde
La recta verde aumenta tres Y por cada X, por lo que su pendiente es 3. Además, uno de sus puntos es (2,2), por tanto:
Recta roja
La recta roja disminuye dos Y por cada X, así que su pendiente es equivalente a -2. Y el punto (0,-2) pertenece a esta recta, por tanto:

