En esta página encontrarás la explicación de la regla (o ley) del paralelogramo. Además, podrás ver varios ejemplos de sumas y restas vectoriales mediante la regla del paralelogramo, así como aplicaciones reales.
Índice
¿Qué es la regla del paralelogramo?
Como ya sabes, las magnitudes vectoriales no se pueden sumar o restar igual que los números reales, porque tienen 2 componentes (en R2) o 3 componentes (en R3) y porque los vectores pueden tener diferente dirección. Por lo tanto, se necesitan otros métodos para hacer operaciones de vectores, como por ejemplo la regla del paralelogramo, que consiste en lo siguiente:
En matemáticas, la regla del paralelogramo es un procedimiento que permite sumar o restar dos vectores a partir de su representación gráfica.
Seguramente el método del paralelogramo es el que más se usa en la suma y la resta de vectores (de manera gráfica), ya que se trata de una técnica muy fácil de utilizar. Por ejemplo, en física se utiliza para sumar y restar fuerzas.
Por otro lado, a regla varia ligeramente según si queremos sumar o restar vectores, así que a continuación te explicamos las dos versiones por separado.
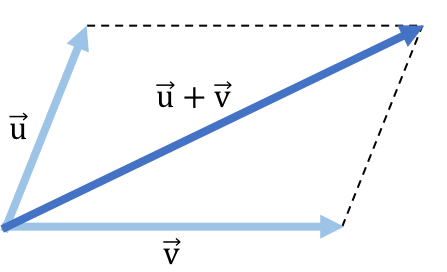
Regla del paralelogramo para sumar dos vectores
Si queremos sumar dos vectores gráficamente, los pasos para aplicar la regla o ley del paralelogramo son:
- En primer lugar, dibujamos los vectores y los posicionamos en el mismo punto de aplicación, es decir, situamos los orígenes de los dos vectores en el mismo punto.
- Después dibujamos en el extremo de un vector una recta paralela al otro vector. Y repetimos el paso con el otro vector. De manera que obtendremos el dibujo de un paralelogramo (de ahí viene el nombre de la regla).
- Finalmente, el vector resultante de la suma será la diagonal del paralelogramo que va desde el origen común de los vectores hasta el punto donde se cruzan las dos rectas paralelas.
En el siguiente ejemplo genérico puedes ver cómo se utiliza la regla del paralelogramo:
Si quieres practicar con la regla del paralelogramo, en el siguiente enlace puedes consultar más ejemplos y varios ejercicios resueltos de suma de vectores. En esta página también encontrarás otros métodos para sumar vectores gráficamente e incluso cómo se suman numéricamente.
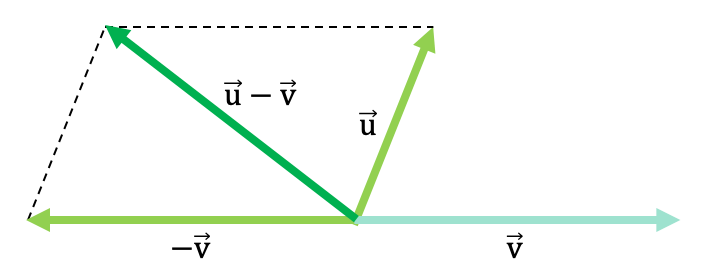
Regla del paralelogramo para restar dos vectores
La regla o método del paralelogramo también sirve para restar dos vectores a partir de un gráfico. Así pues, los pasos para restar vectorialmente son:
- Primeramente, representamos los dos vectores en la gráfica y los posicionamos en el mismo punto de aplicación, es decir, situamos los orígenes de los dos vectores en el mismo punto.
- En segundo lugar, dibujamos el vector opuesto del vector que resta en la operación, o dicho con otras palabras, invertimos el vector que está restando.
- Luego dibujamos una recta paralela al vector cambiado de signo en el extremo del vector que suma . Y repetimos el proceso con el otro vector. De forma que obtendremos el dibujo de un paralelogramo (por eso el nombre de la regla).
- Por último, el resultado de la resta será el vector que va desde el origen en común de los dos vectores hasta el punto donde se cruzan las dos rectas paralelas.
Fíjate en el siguiente ejemplo genérico en el que se restan dos vectores a través de la ley del paralelogramo:
En el siguiente enlace puedes ver más ejemplos de restas vectoriales con la regla del paralelogramo, asimismo, podrás practicar con ejercicios resueltos de resta de vectores. Además, encontrarás otras técnicas para restar vectores a partir de su gráfica y, finalmente, cómo se restan numéricamente.
Finalmente, si te ha resultado útil la explicación de esta técnica, seguramente también te interese saber qué es la regla de la mano derecha. En la página del enlace podrás ver en qué consiste, para qué operación vectorial se utiliza y las diferentes variantes que existen de esta regla.

