Qué son y cómo calcular las componentes de un vector

En esta página encontrarás la explicación de qué son las componentes (o coordenadas) de un vector. También, podrás ver cómo se calculan a partir de dos puntos e incluso cómo se descomponen a través de su módulo y su ángulo. Además, hallarás ejemplos y ejercicios resueltos paso a paso.

¿Qué son las componentes de un vector?

Las componentes de una vector son las proyecciones de un vector sobre los ejes cartesianos. Por lo tanto, la proyección del vector sobre el eje de las abscisas es la componente X del vector y, del mismo modo, la proyección del vector sobre el eje de las ordenadas es la componente Y del vector.

Las componentes de un vector también se pueden llamar coordenadas de un vector.

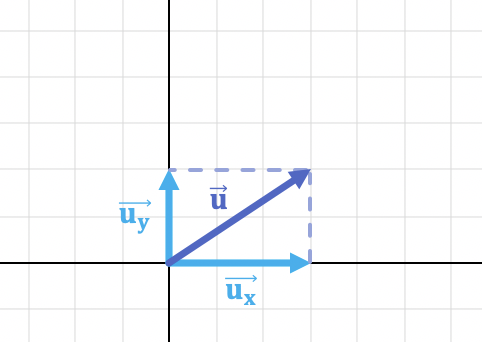
Por ejemplo, la componente horizontal y la componente vertical del vector de la imagen anterior son:

De manera que el vector es:

Por lo tanto, las componentes de un vector también se pueden definir como la representación de un vector en un sistema de coordenadas. Evidentemente, si se trata de un sistema bidimensional (en r2) el vector tendrá dos componentes, en cambio, si es una base tridimensional (en r3) el vector estará formado por tres componentes.

Las componentes cartesianas de un vector son tan importantes porque con ellas podemos saber las características del vector, que principalmente son la dirección, el sentido y el módulo (o magnitud) del vector. Además, sirven para hacer operaciones de vectores.

Cómo calcular las componentes de un vector a partir de dos puntos

Acabamos de ver cómo hallar las coordenadas de un vector gráficamente, sin embargo, también podemos determinar sus componentes numéricamente.

Para calcular las componentes de un vector numéricamente necesitamos saber dos puntos: su origen y su extremo, o dicho de otra forma, dónde empieza y dónde acaba. Ya que las componentes de un vector son las coordenadas que obtenemos de restar su extremo menos su origen.

Por ejemplo, vamos a calcular el vector cuyo origen es el punto A(3,1) y su extremo el punto B(5,4):

Como puedes ver, determinar las componentes de un vector no es muy difícil, sin embargo, tiene bastante importancia. Por ejemplo, uno de los tipos de vectores más utilizados son los vectores perpendiculares (u ortogonales); pues bien, si entiendes qué son las coordenadas de un vector resulta muy fácil calcular vectores perpendiculares. Puedes ver cómo se hace en la explicación de los vectores ortogonales.

Cómo calcular las componentes de un vector a partir de su módulo y su ángulo

También se puede encontrar las componentes de un vector a partir de su módulo y el ángulo que forma con el eje X. Este proceso se denomina descomposición vectorial.

De manera que se pueden calcular las componentes X e Y del vector con las razones trigonométricas del coseno y del seno:

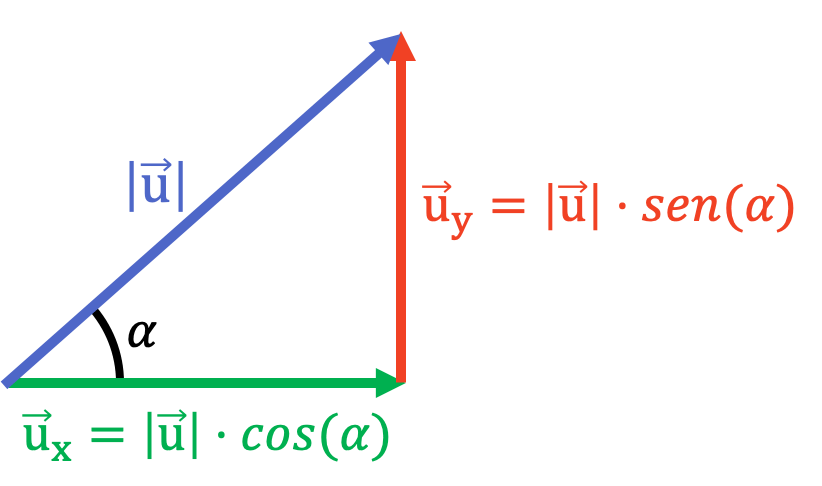
Como puedes ver en la imagen, el módulo de un vector junto con sus componentes completan un triángulo rectángulo, por lo que se pueden aplicar las fórmulas elementales de la trigonometría.

Si no recuerdas cómo se calcula el módulo de un vector, puedes consultar qué es el módulo de un vector. Aquí encontrarás la fórmula del módulo de un vector, junto con ejemplos, ejercicios resueltos paso a paso y todas las propiedades del módulo de un vector. Es una explicación muy completa así que lo entenderás a la perfección. ✅

A diferencia del módulo de un vector que siempre es positivo, sus componentes sí que pueden ser negativas porque el seno y el coseno pueden tomar valores negativos.

A modo de ejemplo, vamos a hacer la descomposición vectorial del vector cuyos módulo y ángulo con el eje OX son:

La componente X del vector es igual al módulo multiplicado por el coseno del ángulo:

Y la componente Y del vector es igual al proucto del módulo por el seno del ángulo:

Así que las coordenadas del vector son: