En esta página encontrarás cuáles son las posiciones relativas de una recta y un plano. Explicamos cómo se calcula la posición relativa entre una recta y un plano (2 métodos) y, además, podrás ver ejemplos y ejercicios resueltos paso a paso.
Índice
¿Cuáles son las posiciones relativas entre una recta y un plano?
Antes de ver todas las posibles posiciones relativas entre una recta y un plano, evidentemente debes saber qué son las rectas y qué es el plano. Por lo que si aún no tienes estos dos conceptos muy claros, te recomendamos que primero le eches un vistazo a las páginas enlazadas donde se explica detalladamente.
Así pues, en geometría analítica solo existen tres posiciones relativas en el espacio entre una recta y un plano:
- Recta contenida en el plano: cuando la recta está contenida dentro del plano significa que tienen infinitos puntos en común.
- Recta y plano paralelos: una recta y un plano son paralelos cuando no tienen ningún punto en común.
- Recta y plano secantes: una recta y un plano son secantes cuando la recta corta al plano en algún punto. Por lo tanto, solamente tienen un punto en común.
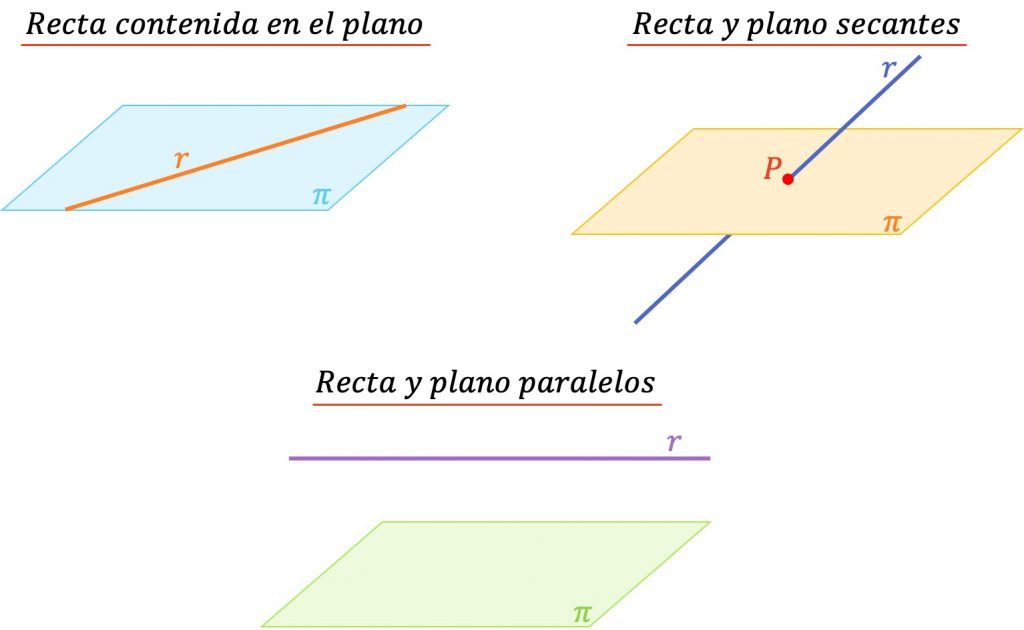
Por otro lado, cuando la recta esté contenida en el plano o cuando sean paralelos entre sí, el ángulo que formarán será de 0º. En cambio, cuando la recta y el plano son secantes el ángulo entre los dos elementos geométricos puede ir desde 0º (no incluido) hasta 90º (incluido).
¿Cómo calcular la posición relativa de una recta y un plano?
Principalmente, existen dos métodos para hallar la posición relativa entre una recta y un plano en el espacio: por rangos o por vectores.
Cuando la recta está expresada en forma de ecuación implícita (o general) es más fácil utilizar el método de los rangos. Por contra, si la recta viene dada con otro tipo de ecuación, por ejemplo cuando está en forma de ecuación vectorial, paramétrica o continua, es más rápido usar el método de los vectores.
Si no recuerdas cómo son las ecuaciones de la recta, te dejamos una página donde puedes consultar todas las ecuaciones de la recta. Aquí encontrarás cuáles son todas las ecuaciones de la recta, una fórmula para hallar de manera rápida la ecuación de una recta que pasa por dos puntos, ejemplos y ejercicios resueltos paso a paso.
Por lo tanto, es más conveniente utilizar un método u otro dependiendo del problema, por eso mismo te recomendamos que sepas hacer los dos procedimientos. A continuación tienes la explicación de ambos métodos con ejemplos.
Cuando la recta está en forma de ecuación implícita (o general)
Una forma de determinar la posición relativa entre una recta y un plano es calculando el rango de dos matrices.
Si la recta está definida por sus ecuaciones implícitas (o generales):
Y el plano también está expresado en forma de ecuación general:
Llamaremos A a la matriz compuesta por los coeficientes A, B y C de las ecuaciones del plano y de la recta:
Y la matriz A’ será la matriz ampliada con todos los coeficientes de las dos ecuaciones:
Entonces, la posición relativa entre la recta y el plano viene determinada por el valor del rango de las dos matrices anteriores según la siguiente tabla:
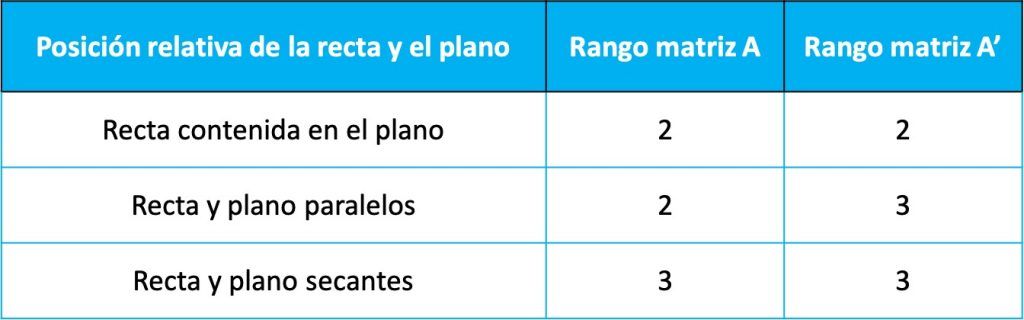
Que las posiciones relativas dependen de los rangos de estas dos matrices se puede demostrar a partir del toerema de Rouché-Frobenius (un teorema que sirve para resolver sistemas de ecuaciones lineales). Sin embargo, en esta página no haremos la demostración porque no es necesario saberla y tampoco aporta demasiado.
Ejemplo de cómo hallar la posición relativa de una recta y un plano por rangos
Para que puedas ver exactamente cómo se hace, vamos a resolver un ejercicio a modo de ejemplo:
- Estudia la posición relativa entre la siguiente recta y el siguiente plano:
La recta esta definida por dos planos secantes, es decir, está expresada en forma de ecuación implícita. Por lo tanto, usaremos el método de los rangos para estudiar la posición relativa entre la recta y el plano.
Lo primero que debemos hacer es construir la matriz A y la matriz ampliada A’ con los coeficientes de las ecuaciones:
Y ahora tenemos que calcular el rango de cada matriz. Primero hallamos el rango de la matriz A por determinantes:
El determinante de la matriz A es nulo pero contiene una submatriz 2×2 cuyo determinante es diferente de cero, con lo que se trata de una matriz de rango 2.
Por otro lado, también tenemos que calcular el rango de la matriz A’. Y el rango de la matriz ampliada A’ siempre será como mínimo el mismo de la matriz A, de modo que únicamente debemos comprobar si es de rango 3 o 2:
En cambio, la matriz ampliada A’ sí que tiene un subdeterminante 3×3 que da distinto de 0, así que es de rango 3.
Por lo tanto, como la matriz A es de rango 2 y la matriz A’ de rango 3, la recta y el plano son paralelos.
Cuando la recta está en forma de otro tipo de ecuación
Cuando la recta está expresada mediante una ecuación que no sea la implícita, ya sea la ecuación vectorial, la paramétrica o la continua, es mejor emplear el método que explicamos a continuación.
De modo que si la recta viene dada en forma de ecuación vectorial, ecuaciones paramétricas o ecuación continua, quiere decir que conocemos un punto que pertenece a la recta y, además, su vector director.
Por otra parte, también sabemos cuál es el vector normal (o perpendicular) al plano:
Entonces, a partir de los 2 vectores y del punto de la recta, se puede calcular la posición relativa entre la recta y el plano de la siguiente manera:
- Si el producto escalar entre el vector director de la recta y el vector normal al plano es diferente de cero, significa que la recta es secante al plano.
- Pero si el producto escalar entre el vector director de la recta y el vector normal al plano es igual a cero hay dos posibilidades: la recta está contenida en el plano o son paralelos. Y para saber de qué caso se trata, debemos sustituir las coordenadas de un punto de la recta en la ecuación del plano.
- Si el punto cumple con la ecuación del plano, la recta está contenida en el plano.
- En cambio, si el punto no cumple la ecuación del plano, la recta y el plano son paralelos.
Ejemplo de cómo determinar la posición relativa de una recta y un plano por vectores
Una vez hemos visto la teoría sobre este método, veamos ahora un ejercicio resuelto paso a paso:
- Halla la posición relativa entre la siguiente recta y el siguiente plano:
En primer lugar, la recta está definida en forma de ecuaciones paramétricas, por lo tanto, su vector director y un punto por el que pasa son:
Y, por otro lado, el vector normal al plano es:
Una vez sabemos el vector director de la recta y el vector normal al plano, tenemos que calcular el producto escalar entre ellos dos:
El resultado del producto escalar es nulo, de modo que la recta solo puede esta contenida en el plano o ser paralela a él. Así pues, para averiguar qué caso es, sustituimos las coordenadas cartesianas del punto de la recta en la ecuación del plano:
Al sustituir el punto de la recta en la ecuación del plano obtenemos una igualdad, por lo tanto, el punto sí que cumple con la ecuación del plano y, en consecuencia, la recta está contenida en el plano.

Buenísimo me fue muy útil
¡Gracias Claudia!
Aquí, salvando EVAUs. ¡Muchas gracias!