En esta página se explica las diferentes posiciones relativas que existen entre una recta y una circunferencia. Además, podrás ver cómo hallar la posición relativa entre una recta y una circunferencia.
Índice
¿Cuáles son las posiciones relativas de una recta y una circunferencia?
En geometría analítica, la posición relativa de una recta respecto a una circunferencia solo puede ser exterior, tangente o secante:
- Exterior: cuando la distancia entre la recta y el centro de la circunferencia es mayor que el radio.
- Tangente: cuando la distancia entre la recta y el centro de la circunferencia es igual que el radio.
- Secante: cuando la distancia entre la recta y el centro de la circunferencia es menor que el radio.
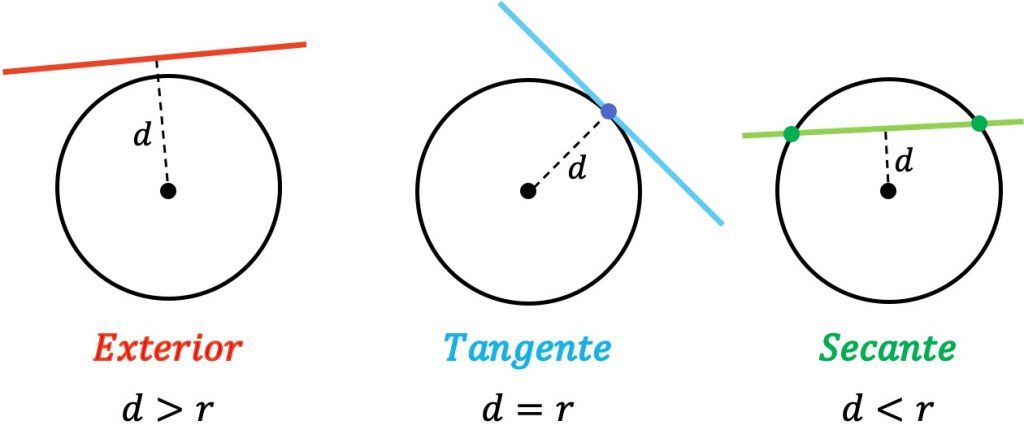
Por lo tanto, si una recta es exterior a una circunferencia no la corta en ningún punto. En cambio, cuando la recta es tangente a la circunferencia ambas tienen un único punto en común. Y, por último, una recta es secante a una circunferencia cuando la interseca en dos puntos distintos.
¿Cómo determinar la posición relativa entre una recta y una circunferencia?
Hay dos maneras de saber cuál es la posición relativa de una recta respecto a una circunferencia en el plano: una es calculando la distancia entre la recta y el centro de la circunferencia, y la otra forma es resolviendo un sistema de ecuaciones compuesto por la ecuación de la recta y la ecuación de la circunferencia.
A continuación vamos a ver exactamente en qué consiste cada método.
Método 1: Distancia entre la recta y el centro de la circunferencia
Cómo hemos visto en la explicación del concepto de posición relativa entre una recta y una circunferencia, la distancia entre una recta y el centro de una circunferencia indica qué tipo de posición relativa se trata.
Por tanto, este método consiste en hallar la distancia que hay entre la recta y el centro de la circunferencia. Evidentemente, para poder hacer esto debes saber cómo calcular la distancia entre un punto y una recta, en esta página puedes consultar cómo se hace, así como ejemplos y ejercicios resueltos para practicar.
Así pues, en función del resultado de la distancia obtenida se tratará de un caso u otro:
- La recta será exterior a la circunferencia si la distancia obtenida es más grande que el radio de la circunferencia.
- La recta será tangente a la circunferencia si la distancia obtenida es equivalente al radio de la circunferencia.
- La recta será secante a la circunferencia si la distancia obtenida es más pequeña que el radio de la circunferencia.
Método 2: Resolver un sistema de ecuaciones
Otra forma de averiguar la posición relativa de una recta respecto a una circunferencia es mediante un sistema de ecuaciones formado por la ecuación de la recta y la ecuación de la circunferencia. Obviamente, para poder aplicar este método debes conocer cuál es la ecuación de la circunferencia y cuál es la fórmula de la ecuación de la recta.
Dependiendo de cuántas soluciones tenga el sistema de ecuaciones, estaremos delante de un caso u otro:
- Si el sistema de ecuaciones no tiene solución significa que la recta y la circunferencia no tienen ningún punto en común, por lo que la recta es exterior a la circunferencia.
- Si el sistema de ecuaciones tiene 1 solución implica que la recta y la circunferencia tienen un punto en común, así que la recta es tangente a la circunferencia.
- Si el sistema de ecuaciones tiene 2 soluciones quiere decir que la recta y la circunferencia tienen dos puntos en común, de modo que la recta es secante a la circunferencia.
