▷ Distancia entre un Punto y una Recta (fórmula y ejemplos)

Aquí encontrarás la fórmula que sirve para calcular la distancia entre un punto y una recta. Además, podrás ver varios ejemplos y ejercicios resueltos de distancias entre puntos y rectas e, incluso, las aplicaciones que tiene esta operación (por ejemplo hallar la distancia entre rectas paralelas).

Índice

Fórmula de la distancia entre un punto y una recta

La distancia entre un punto y una recta es la distancia más corta que existe entre ese punto y la recta. Matemáticamente, esta distancia mínima es equivalente a la longitud del segmento trazado desde el punto hasta la recta y que es perpendicular a la recta.

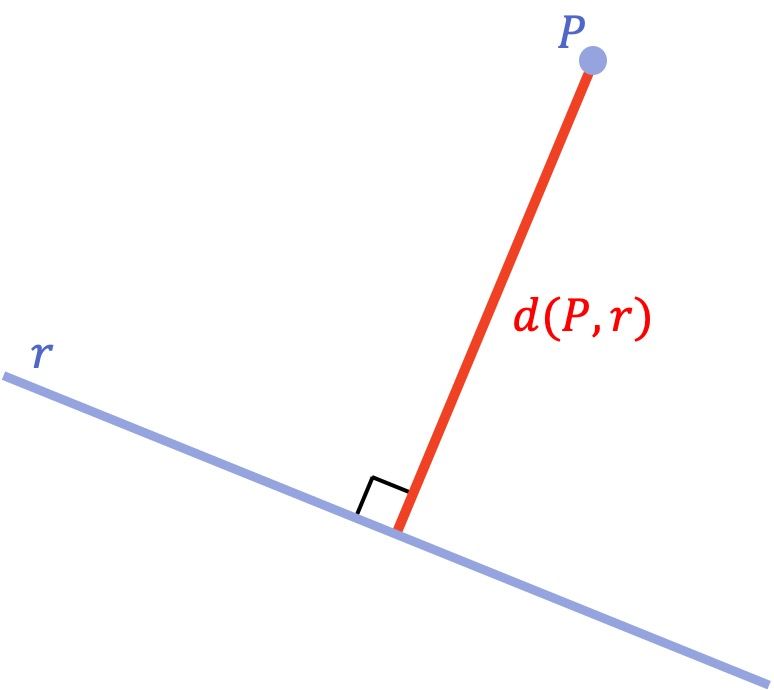
cuál es la distancia entre un punto y una recta

Una vez visto el concepto geométrico de distancia entre un punto y una recta, veamos cuál es la fórmula que sirve para calcular dicha distancia:

Dadas la ecuación implícita (o general) de una recta y las coordenadas de un punto cualquiera en un plano:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

La fórmula de la distancia entre un punto y una recta es:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Importante: fíjate que la ecuación de la recta en la fórmula está en forma de ecuación implícita (o general), por lo tanto, si tenemos la recta expresada en otro tipo de ecuación primero tenemos que pasarla a su ecuación implícita y luego ya podremos aplicar la fórmula.

Ejemplo de cómo calcular la distancia entre un punto y una recta

A continuación puedes ver un ejemplo de cómo se calcula la distancia entre un punto y una recta:

Halla la distancia entre el punto $P$ y la recta $r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Para calcular la distancia entre el punto y la recta, simplemente debemos aplicar su fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Ahora sustituimos cada término por su valor:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

Y finalmente calculamos la distancia:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Distancia entre dos rectas paralelas

Una de las aplicaciones del cálculo de la distancia entre una recta y un punto es encontrar la distancia entre rectas paralelas.

Evidentemente, para entender el concepto que explicaremos a continuación debes saber qué son las rectas paralelas, así que si no sabes exactamente su definición te dejamos un enlace donde te lo explicamos detalladamente y también podrás ver ejemplos de rectas paralelas.

Para hallar la distancia entre dos rectas paralelas, solo tenemos que coger un punto de cualquiera de las dos rectas y calcular la distancia que hay desde ese punto hasta la otra recta.

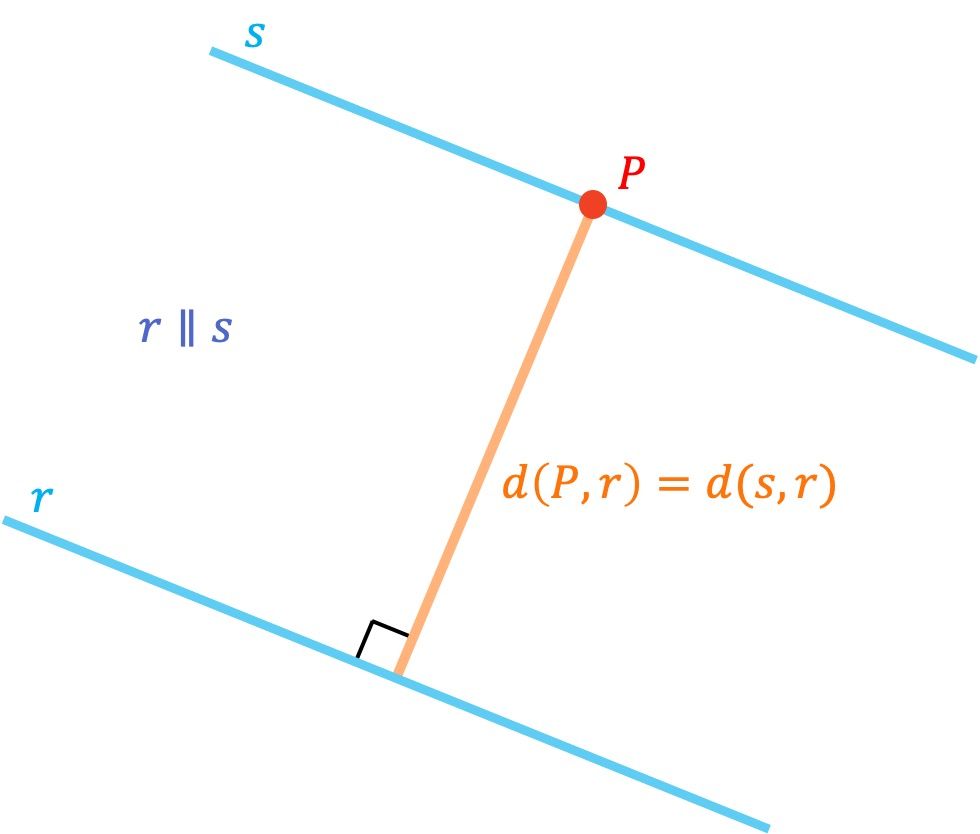
distancia de entre un punto y una recta online

De modo que para determinar la distancia entre dos rectas paralelas también se utiliza la fórmula de la distancia entre una recta y un punto.

Por otro lado, si al usar la fórmula obtenemos una distancia de 0 unidades, significa que las rectas se tocan en algún punto y, por tanto, las rectas no son paralelas, sino que son secantes, coincidentes o perpendiculares. Si quieres puedes consultar las diferencias entre este tipo de rectas en nuestra web.

Veamos pues cómo se resuelve un problema de distancia entre dos rectas paralelas a través de un ejemplo:

Encuentra la distancia entre las siguientes dos rectas paralelas:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Lo primero que debemos hacer es conseguir un punto de una de las rectas (la que quieras). En este caso calcularemos un punto de la recta $s.$ Para ello tenemos que dar un valor a una de las variables, nosotros haremos por ejemplo $x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Y ahora despejamos la otra variable ( $y$ ) de la ecuación obtenida para saber cuánto vale en este punto:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Por tanto, el punto obtenido de la recta $s$ es:

$P(0,-2)$

Y una vez ya tenemos un punto de una recta, calculamos la distancia de ese punto a la otra recta mediante la fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Ejercicios resueltos de distancia entre un punto y una recta

Ejercicio 1

Calcula la distancia entre el punto $P$ y la recta $r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

Ver solución

Para encontrar la distancia entre un punto y una recta, solamente debemos aplicar su fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Sustituimos cada término por su valor y calculamos la distancia:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Ejercicio 2

¿Cuál es la distancia entre el punto $P$ y la recta $r$ ?

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

Ver solución

En este caso, la ecuación de la recta está en forma implícita (o general). En cambio, para poder utilizar la fórmula de la distancia de un punto a una recta, la recta debe estar expresada en forma de ecuación implícita. De manera que primero debemos transformar la recta y pasarla a ecuación implícita (basta con pasar todos los términos a un mismo lado de la ecuación):

$r: \ 3x+y-5=0$

Y una vez la recta ya está en forma explícita, ya podemos utilizar la fórmula de la distancia entre un punto y una recta:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Así que sustituimos cada término por su valor y calculamos la distancia:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Ejercicio 3

¿Cuál es la distancia entre las siguientes dos rectas?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

Ver solución

Antes de nada, vamos a comprobar que sean dos rectas paralelas. Para ello, los coeficientes de las variables $x$ e $y$ deben ser proporcionales entre sí pero no con los términos independientes:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

Efectivamente, las rectas son paralelas, así que podemos aplicar el procedimiento.

Ahora debemos conseguir un punto de una de las rectas (la que quieras). En este caso calcularemos un punto de la recta $s.$ Para ello tenemos que otorgar un valor a una de las variables, nosotros haremos por ejemplo $x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

Y ahora despejamos la otra variable ( $y$ ) de la ecuación obtenida para averiguar su valor en este punto:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

De modo que el punto obtenido de la recta $s$ es:

$P(0,-1)$

Una vez conocemos un punto de una recta, calculamos la distancia desde ese punto hasta la otra recta con la fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Ejercicio 4

Calcula el valor de la incógnita $k$ para que la distancia entre el punto $P$ y la recta $r$ sea de 5 unidades.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

Ver solución

Primero debemos aplicar la fórmula de la distancia entre un punto y una recta:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Ahora sustituimos cada término por su valor y simplificamos la expresión:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

El enunciado del problema nos dice que la distancia entre el punto y la recta debe ser igual a 5, por lo que igualamos la expresión anterior a 5:

$\cfrac{\lvert -49+k\rvert}{13}=5$

Y resolvemos la ecuación resultante. En el numerador de la fracción hay un valor absoluto, por tanto, debemos analizar por separado cuando el valor absoluto es positivo y cuando es negativo:

$\cfrac{+(-49+k)}{13}=5$